河北省2024年中考数学模拟试卷(三)
试卷更新日期:2024-03-24 类型:中考模拟
一、单选题
-
1. 下列各数中,比小的数是( )A、0 B、 C、-1 D、12. 如图,∠AOB的大小为( )
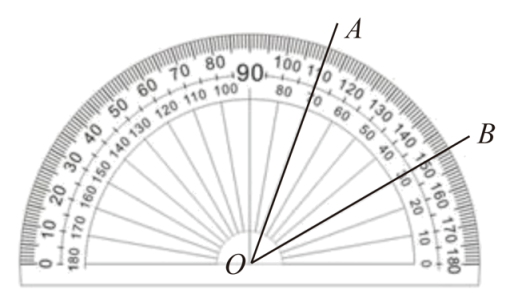 A、 B、 C、 D、3. 小化将一张如图所示的矩形纸片沿对角线剪开,他利用所得的两个直角三角形进行图形变换,构成了下列四个图形,这四个图形中不是轴对称图形的是( )
A、 B、 C、 D、3. 小化将一张如图所示的矩形纸片沿对角线剪开,他利用所得的两个直角三角形进行图形变换,构成了下列四个图形,这四个图形中不是轴对称图形的是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 今年以来,河北持续推进学雷锋志愿服务活动,通过抓队伍,建平台、强阵地,更好地发挥党员干部模范带头作用,努力形成人人学雷锋、人人做雷锋、人人敬雷锋的生动局面.目前,全省共有1155万多名志愿者、5万多个志愿服务组织.其中数据1155万可以表示为( )A、 B、 C、 D、5. 如图,从地观测地,发现地在地的北偏东方向上,则从地观测地,可知地在地的( )
4. 今年以来,河北持续推进学雷锋志愿服务活动,通过抓队伍,建平台、强阵地,更好地发挥党员干部模范带头作用,努力形成人人学雷锋、人人做雷锋、人人敬雷锋的生动局面.目前,全省共有1155万多名志愿者、5万多个志愿服务组织.其中数据1155万可以表示为( )A、 B、 C、 D、5. 如图,从地观测地,发现地在地的北偏东方向上,则从地观测地,可知地在地的( ) A、北偏东方向上 B、南偏西方向上 C、北偏东方向上 D、南偏西方向上6. 如图所示的几何体是由9个大小相同的小正方体组成的,将小正方体①移走后,所得几何体的三视图没有发生变化的是( )
A、北偏东方向上 B、南偏西方向上 C、北偏东方向上 D、南偏西方向上6. 如图所示的几何体是由9个大小相同的小正方体组成的,将小正方体①移走后,所得几何体的三视图没有发生变化的是( )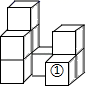 A、主视图和左视图 B、主视图和俯视图 C、左视图和俯视图 D、主视图、左视图、俯视图7. 解方程 ,以下去括号正确的是( )A、 B、 C、 D、8. 如图所示的扇形统计图描述了某校学生对课后延时服务的打分情况(满分5分),则所打分数的众数为( )
A、主视图和左视图 B、主视图和俯视图 C、左视图和俯视图 D、主视图、左视图、俯视图7. 解方程 ,以下去括号正确的是( )A、 B、 C、 D、8. 如图所示的扇形统计图描述了某校学生对课后延时服务的打分情况(满分5分),则所打分数的众数为( ) A、5分 B、4分 C、3分 D、45%9. 如图,内接于⊙ , 连接 , 则( )
A、5分 B、4分 C、3分 D、45%9. 如图,内接于⊙ , 连接 , 则( )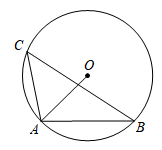 A、 B、 C、 D、10. 定理:三角形的内角和是180°.
A、 B、 C、 D、10. 定理:三角形的内角和是180°.已知:是的三个内角.
求证: .
有如下四个说法:①*表示内错角相等,两直线平行;②@表示;③上述证明得到的结论,只有在锐角三角形中才适用;④上述证明得到的结论,适用于任何三角形.其中正确的是( )

证明:如图,过点E作直线 ,
使得 ,
∴(*),
,
∴ .
A、①② B、②③ C、②④ D、①③11. 以下是代数式排乱的化简步骤:①;
②;
③;
④ .
则正确化简步骤的顺序是( )
A、①→③→④→② B、③→①→④→② C、③→④→①→② D、①→④→③→②12. 要得知某一池塘两端A,B的距离,发现其无法直接测量,两同学提供了如下间接测量方案.方案Ⅰ:如图1,先过点B作 , 再在上取C,D两点,使 , 接着过点D作的垂线 , 交的延长线于点E,则测量的长即可;
方案Ⅱ:如图2,过点B作 , 再由点D观测,用测角仪在的延长线上取一点C,使 , 则测量的长即可.
对于方案Ⅰ、Ⅱ,说法正确的是( )
 A、只有方案Ⅰ可行 B、只有方案Ⅱ可行 C、方案Ⅰ和Ⅱ都可行 D、方案Ⅰ和Ⅱ都不可行13. 一大门栏杆的平面示意图如图所示,垂直地面于点 , 平行于地面 , 若 , 则的度数是( )
A、只有方案Ⅰ可行 B、只有方案Ⅱ可行 C、方案Ⅰ和Ⅱ都可行 D、方案Ⅰ和Ⅱ都不可行13. 一大门栏杆的平面示意图如图所示,垂直地面于点 , 平行于地面 , 若 , 则的度数是( ) A、110° B、120° C、130° D、135°14. 某校举办的知识竞赛,共道题,规定答对一道题加x分,答错一道题(不答按错)扣分,小明答错了2道题,他得到的分数是( )A、 B、 C、 D、15. 如图,平行于y轴的直线分别交 与 的图象(部分)于点A、B,点C是y轴上的动点,则 的面积为( )
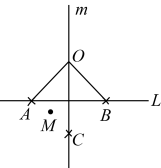
A、110° B、120° C、130° D、135°14. 某校举办的知识竞赛,共道题,规定答对一道题加x分,答错一道题(不答按错)扣分,小明答错了2道题,他得到的分数是( )A、 B、 C、 D、15. 如图,平行于y轴的直线分别交 与 的图象(部分)于点A、B,点C是y轴上的动点,则 的面积为( ) A、 B、 C、 D、16. 对于直线L和直线L外的一点O,按下列步骤完成了尺规作图:(1)在直线L的另一侧取点M;(2)以O为圆心,为半径作弧与L交于A,B两点;(3)分别以A,B为圆心,大于为半径作弧,两弧交于点C;(4)过点O和C作直线m.问题:“在直线m上任取一点P(点P不在L上),连接 , , 过点A作直线n与直线垂直,设是 , 直线n与所夹的锐角是 , 求x与y的数量关系.”下面是三个同学的答案,甲: , 乙: , 丙: .
A、 B、 C、 D、16. 对于直线L和直线L外的一点O,按下列步骤完成了尺规作图:(1)在直线L的另一侧取点M;(2)以O为圆心,为半径作弧与L交于A,B两点;(3)分别以A,B为圆心,大于为半径作弧,两弧交于点C;(4)过点O和C作直线m.问题:“在直线m上任取一点P(点P不在L上),连接 , , 过点A作直线n与直线垂直,设是 , 直线n与所夹的锐角是 , 求x与y的数量关系.”下面是三个同学的答案,甲: , 乙: , 丙: .对于三人的答案,下列结论正确的是( )
 A、只有甲的答案正确 B、甲和乙的答案合在一起才正确 C、甲和丙的答案合在一起才正确 D、甲乙丙的答案合在一起才正确
A、只有甲的答案正确 B、甲和乙的答案合在一起才正确 C、甲和丙的答案合在一起才正确 D、甲乙丙的答案合在一起才正确二、填空题
-
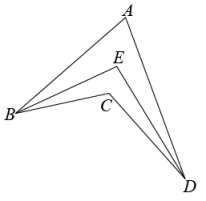
17. 如图,用铁丝折成一个四边形ABCD(点C在直线BD的上方),且∠A=70°,∠BCD=120°,若使∠ABC、∠ADC平分线的夹角∠E的度数为100°,可保持∠A不变,将∠BCD (填“增大”或“减小”)°.
 18. 嘉琪准备完成题目:解一元二次方程 . 若“□”表示一个字母,且一元二次方程有实数根,则“”的最大值为 , 此时方程的解为 .19. 如图,水池中心点O处竖直安装一水管,水管喷头喷出抛物线形水柱,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点O在同一水平面.安装师傅调试发现,喷头高时,水柱落点距O点;喷头高时,水柱落点距O点 . 那么喷头高m时,水柱落点距O点 .
18. 嘉琪准备完成题目:解一元二次方程 . 若“□”表示一个字母,且一元二次方程有实数根,则“”的最大值为 , 此时方程的解为 .19. 如图,水池中心点O处竖直安装一水管,水管喷头喷出抛物线形水柱,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点O在同一水平面.安装师傅调试发现,喷头高时,水柱落点距O点;喷头高时,水柱落点距O点 . 那么喷头高m时,水柱落点距O点 .
三、解答题
-
20. 如图,将数轴上与6两点间的线段六等分,这五个等分点所对应的数依次为 , , , , .
 (1)、;(2)、计算: .21. 如图,公园里有两块边长分别为a,b的正方形区域A、B,其中阴影部分M为雕塑区,面积为m,其他部分种植花草.
(1)、;(2)、计算: .21. 如图,公园里有两块边长分别为a,b的正方形区域A、B,其中阴影部分M为雕塑区,面积为m,其他部分种植花草.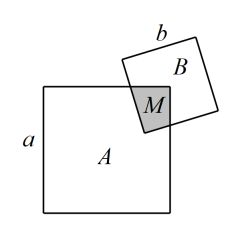 (1)、用含a,b,m的代数式表示种植花草的面积;(2)、若正方形A的一个顶点恰为正方形B的中心,a比b大20,M的面积是A的 , 求a的值.22. 某乒乓球俱乐部有名男队员和名女队员可参加对外比赛,其中有名男队员和名女队员使用左手打球.现计划用这名队员组成混合双打组合.(以下简称混双组合:就是由一名男队员和一名女队员组成)(1)、可以有多少种不同的混双组合?如果从这些组合中任选个参加比赛,那么选中的组合中正好有一名左手队员和一名右手队员的概率是多少?(2)、实际运作中,通过各种组合之间的比赛,最终确定了个组合,其中有一个组合正好是男号与女号组成的(我们称为“一号组合”).如果这三个组合通过抓阉(jiu)方式决定哪一组由张岩教练指导,直接写出“一号组合”选中张岩教练的概率是多少?23. 发现:当两个不同的正整数同为偶数或奇数时,这两个数之和与这两个数之差的平方差一定能被4整除,且这两个数的积可以表示为两个正整数的平方差.
(1)、用含a,b,m的代数式表示种植花草的面积;(2)、若正方形A的一个顶点恰为正方形B的中心,a比b大20,M的面积是A的 , 求a的值.22. 某乒乓球俱乐部有名男队员和名女队员可参加对外比赛,其中有名男队员和名女队员使用左手打球.现计划用这名队员组成混合双打组合.(以下简称混双组合:就是由一名男队员和一名女队员组成)(1)、可以有多少种不同的混双组合?如果从这些组合中任选个参加比赛,那么选中的组合中正好有一名左手队员和一名右手队员的概率是多少?(2)、实际运作中,通过各种组合之间的比赛,最终确定了个组合,其中有一个组合正好是男号与女号组成的(我们称为“一号组合”).如果这三个组合通过抓阉(jiu)方式决定哪一组由张岩教练指导,直接写出“一号组合”选中张岩教练的概率是多少?23. 发现:当两个不同的正整数同为偶数或奇数时,这两个数之和与这两个数之差的平方差一定能被4整除,且这两个数的积可以表示为两个正整数的平方差.验证:如,能被4整除,请把3与1的积写成两个正整数的平方差;
探究:设“发现”中两个正整数分别为m,n,请论证“发现”中的结论正确.
24. 随着 技术的发展,人们对各类 产品的使用充满期待.某公司计划在某地区销售第一款 产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第 ( 为正整数)个销售周期每台的销售价格为 元, 与 之间满足如图所示的一次函数关系.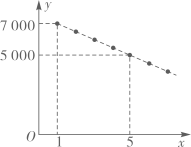 (1)、求 与 之间的关系式;(2)、设该产品在第 个销售周期的销售数量为 (万台), 与 的关系可用 来描述。根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?25. 建大棚种植蔬菜是农民致富的一条好途径.经市场调查发现:搭建一个面积为(为整数)公顷的大棚,前期准备所需总费用由建设费用和内部设备费用两部分组成,其中建设费用与成正比例,内部设备费用与成正比例,部分数据如下:
(1)、求 与 之间的关系式;(2)、设该产品在第 个销售周期的销售数量为 (万台), 与 的关系可用 来描述。根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?25. 建大棚种植蔬菜是农民致富的一条好途径.经市场调查发现:搭建一个面积为(为整数)公顷的大棚,前期准备所需总费用由建设费用和内部设备费用两部分组成,其中建设费用与成正比例,内部设备费用与成正比例,部分数据如下:大棚面积/公顷
3
8
前期准备所需总费用/万元
21
134
(1)、求前期准备所需总费用与之间的函数关系式.(2)、若种植1公顷蔬菜需种子、化肥、农药的开支0.4万元,收获1公顷的蔬菜年均可卖9.4万元.设当年收获蔬菜的总收益(扣除修建和种植成本)为万元,写出与之间的函数关系式.(3)、求种植的面积为多少公顷时,当年收获蔬菜的总收益最大,最大值为多少?26. 如图,矩形ABCD中,AB=4,AD=3,点E在射线CB上运动(可与点C重合),DE的中点为G,将EG绕点E顺时针旋转90°得到EF,再以ED,EF为一组邻边作矩形DEFH. (1)、当点E为BC的中点时,点F到直线BC的距离为;(2)、当点F落在矩形ABCD的边(或边所在的直线)上时,求CE的长;(3)、点E在线段BC(可与点B,C重合)上运动时,直接写出线段CF的最小值.
(1)、当点E为BC的中点时,点F到直线BC的距离为;(2)、当点F落在矩形ABCD的边(或边所在的直线)上时,求CE的长;(3)、点E在线段BC(可与点B,C重合)上运动时,直接写出线段CF的最小值.