备考2024年中考数学探究性训练专题16 分段函数与函数动点问题
试卷更新日期:2024-03-24 类型:二轮复习
一、选择题
-
1. 某书定价8元,如果一次购买10本以上,超过10本部分打八折,那么付款金额 ,与购书数量 之间的函数关系如何,同学们对此展开了讨论:
⑴小明说: 与 之间的函数关系为 ;
⑵小刚说: 与 之间的函数关系为 ;
⑶小聪说: 与 之间的函数关系在 时, ;在 时, ;
⑷小斌说;我认为用下面的列表法也能表示它们之间的关系.
购买量/本
1
2
3
4
…
9
10
11
12
…
付款金额/元
8
16
24
32
…
72
80
86.4
92.8
…
其中,表示函数关系正确的个数有( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
2. 小明同学在研究函数(为常数)时,得到以下四个结论:
①当时,随的增大而增大;②当时,有最小值0,没有最大值;
③该函数的图象关于轴对称;④若该函数的图象与直线(为常数)至少有3个交点,则 . 其中正确的结论是 . (请填写序号)
3. 心理学家研究发现:一般情形下,在一节40分钟的课中,学生的注意力随教师讲课的时间变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持为理想的稳定状态,随后学生的汪意力开始分散.经过实验分析,知学生的注意力指数y随时间x(分钟)的变化规律为:有一道数学竞赛题需要讲解16.5分钟,为了使效果更好,要求学生的注意力指数最低值达到最大.那么,教师经过适当安排,应在上课的第分钟开始讲解这道题.
4. 在数学综合实践课中,小明和同学对类似八下教科书25页例2的问题进行拓展探索:如图1,一根长为5米的木棍斜靠在一竖直的墙上,为4米,如果木棍的顶端沿墙下滑米,底端向外移动米,下滑后的木棍记为 , 则与满足的等式 , 即关于的函数解析式为 , 小明利用画图软件画出了该函数图象如图2,
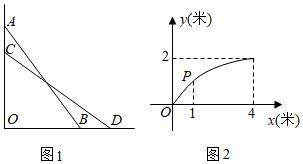 (1)、请写出图象上点的坐标(1,)(2)、根据图象,当的取值范围为时,的周长大于的周长.
(1)、请写出图象上点的坐标(1,)(2)、根据图象,当的取值范围为时,的周长大于的周长.三、数形结合探究题
-
5. 小飞哥根据学习“一次函数”时积累的经验,对函数的图象与性质进行了探究,下面是小飞哥的探究过程,请补充完整:(1)、平面直角坐标系中,画出函数的图象:
①在函数中,自变量的取值范围是;
②列表:
…
0
1
2
3
…
…
0
…
其中,;
③描点、连线,在平面直角坐标系中,画出的图象;
(2)、结合所画函数图象,写出两条不同类型的性质;性质1:;
性质2:;
(3)、小飞哥利用所画函数图象,估算不等式的解集是 .6. 在等腰直角三角形ABC中,AB=AC,∠BAC=90°,点P为射线BA上一个动点,连接PC,点D在直线BC上,且PD=PC。过点P作EP⊥PC于点P,点D,E在直线AC的同侧,且PE=PC,连接BE。请用等式表示线段BE,BP,BC之间的数量关系。小明根据学习函数的经验,对线段BE,BP,BC的长度之间的关系进行了探究。下面是小明的探究过程。请补充完整:
 (1)、对于点PC在射线BA上的不同位置,画图、测量,得到了线段BE,BP,BC的长度的几组值,如下表:
(1)、对于点PC在射线BA上的不同位置,画图、测量,得到了线段BE,BP,BC的长度的几组值,如下表:位置1
位置2
位置3
位置4
位置5
位置6
位置7
位置8
BC/cm
2.83
2.83
2.83
2.83
2.83
2.83
2.83
2.83
BE/cm
2.10
1.32
0.53
0.00
1.32
2.10
4.37
5.6
BP/cm
0.52
1.07
1.63
2.00
2.92
3.48
5.09
5.97
在BE,BP,BC的长度这三个量中,确定的长度是自变量,的长度和的长度都是这个自变量的函数,的长度是常量。
(2)、在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;(3)、结合函数图象,解决问题:请用等式表示线段BE,BP,BC之间的数量关系。7. 如图1,AB为半圆O的直径,半径的长为4cm,点C为半圆上一动点,过点C作CE⊥AB,垂足为点E,点D为弧AC的中点,连接DE,如果DE=2OE,求线段AE的长.小何根据学习函数的经验,将此问题转化为函数问题解决.
小华假设AE的长度为xcm,线段DE的长度为ycm.
(当点C与点A重合时,AE的长度为0cm),对函数y随自变量x的变化而变化的规律进行探究.
下面是小何的探究过程,请补充完整:(说明:相关数据保留一位小数).
 (1)、通过取点、画图、测量,得到了x与y的几组值,如下表:
(1)、通过取点、画图、测量,得到了x与y的几组值,如下表:x/cm
0
1
2
3
4
5
6
7
8
y/cm
0
1.6
2.5
3.3
4.0
4.7
5.8
5.7
当x=6cm时,请你在图中帮助小何完成作图,并使用刻度尺度量此时线段DE的长度,填写在表格空白处:
(2)、在图2中建立平面直角坐标系,描出补全后的表中各组对应值为坐标的点,画出该函数的图象;(3)、结合画出的函数图象解决问题,当DE=2OE时,AE的长度约为cm.8. 如图,点E是矩形ABCD边AB上一动点(不与点B重合),过点E作EF⊥DE交BC于点F,连接DF,已知AB=4cm,AD=2cm,设A,E两点间的距离为xcm,△DEF面积为ycm2 .小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)、确定自变量x的取值范围是;(2)、通过取点、画图、测量、分析,得到了x与y的几组值,如表:x/cm
0
0.5
1
1.5
2
2.5
3
3.5
…
y/cm2
4.0
3.7
3.9
3.8
3.3
2.0
…
(说明:补全表格时相关数值保留一位小数)
(3)、建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象; (4)、结合画出的函数图象,解决问题:当△DEF面积最大时,AE的长度为cm.
(4)、结合画出的函数图象,解决问题:当△DEF面积最大时,AE的长度为cm.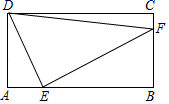 9. 问题探究:嘉嘉同学根据学习函数的经验,对函数y=-2|x|+5的图象和性质进行了探究.下面是嘉嘉的探究过程,请你解决相关问题:(1)、如图,嘉嘉同学在平面直角坐标系中,描出了以表中各对对应值为坐标的点,请你根据描出的点,画出该函数的图象:
9. 问题探究:嘉嘉同学根据学习函数的经验,对函数y=-2|x|+5的图象和性质进行了探究.下面是嘉嘉的探究过程,请你解决相关问题:(1)、如图,嘉嘉同学在平面直角坐标系中,描出了以表中各对对应值为坐标的点,请你根据描出的点,画出该函数的图象:
若A(m,n),B(6,n)为该函数图象上不同的两点,则m= ▲ ;
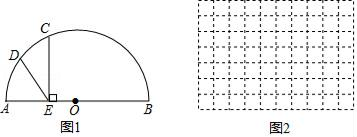
(2)、观察函数y=-2|x|+5的图象,写出该图象的两条性质;(3)、直接写出,当0<-2|x|+5≤3时,自变量x的取值范围.10. 小航在学习中遇到这样一个问题:如图,点C是上一动点,直径 , 过点C作交于点D,O为AB的中点,连接OC,OD,当的面积为时,求线段CD的长.
小航结合学习函数的经验探究此问题,请将下面的探究过程补充完整:
(1)、根据点C在上的不同位置,画出相应的图形,测量、计算线段CD的长度和的面积得到下表的几组对应值(当点C与点A或点B重合时,的面积为0).0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
0
2.0
3.9
5.6
m
7.8
7.9
6.8
0
填空:m=.(结果保留一位小数,参考数据: , )
(2)、将线段CD的长度作为自变量x(cm),的面积是x的函数,记为 , 请在如下平面直角坐标系xOy中画出y关于x的函数图象,并根据图象判断下列说法是否正确.(正确的打“√”,错误的打“×”)①该函数图象为抛物线的一部分;( )
②当时,y随x的增大而增大;( )
③的面积有最大值.( )
(3)、继续在同一坐标系中画出所需的图象,并结合图象直接写出:当的面积为时,线段CD长度的近似值.(结果保留一位小数)11. 如图1,中, , , cm,点D为AB边上的动点(点D不与点A,B重合),过点D作交直线AC于点E.在点D由点A到点B运动的过程中,设cm,cm.根据学习函数的经验,可对函数y随x的变化而变化的情况进行了探究,请将探究过程补充完整: (1)、通过取点、画图、测量或计算,得到了x与y的几组值,如下表:
(1)、通过取点、画图、测量或计算,得到了x与y的几组值,如下表:x/cm
…
1
2
3
…
y/cm
…
0.4
0.8
1.0
m
1.0
0
4.0
…
则表中m的值为.(保留一位小数)
(2)、在图2的平面直角坐标系中,以表格中各对x,y的值为坐标描点,并画出该函数的大致图象;(3)、结合(2)中画出的函数图象,解决问题:当时,AD的长度约为cm.12. 若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数,下面我们参照学习函数的过程与方法,探究分段函数 的图象与性质,探究过程如下,请补充完整.(1)、列表:x
…
0
1
2
3
…
y
…
m
1
2
1
0
1
n
…
其中, , .
(2)、描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示,请画出函数的图象. (3)、研究函数并结合图象与表格,回答下列问题:
(3)、研究函数并结合图象与表格,回答下列问题:①点 ,在函数图象上,则 , ;(填“>”,“=”或“<”)
②当函数值时 ,求自变量x的值;
13. 小东同学根据函数的学习经验,对函数y = + 进行了探究,
下面是他的探究过程:
(1)、已知x=-3时 = 0;x=1 时 = 0,化简:①当x<-3时,y=
②当-3≤x≤1时,y=
③当x>1时,y=
(2)、在平面直角坐标系中画出y = + 的图像,根据图像,写出该函数的一条性质.(3)、根据上面的探究解决,下面问题:已知A(a,0)是x轴上一动点,B(1,0),C(-3,0),则AB+AC的最小值是
14. 在 中, , , ,将 绕点 顺时针旋转,角的两边分别交射线 于 , 两点, 为 上一点,连接 ,且 (当点 , 重合时,点 , 也重合).设 , 两点间的距离为 , , 两点间的距离为 .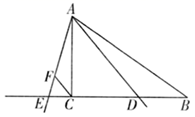
小刚根据学习函数的经验,对因变量 随自变量 的变化而变化的规律进行了探究.
下面是小刚的探究过程,请补充完整.
(1)、列表:下表的已知数据是根据 , 两点间的距离 进行取点,画图,测量分别得到了 与 的几组对应值;0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
6
7
8
6.00
5.76
5.53
5.31
5.09
4.88
4.69
4.50
4.33
4.17
4.02
3.79
3.65
请你通过计算补全表格: ;
(2)、描点、连线:在平面直角坐标系 中,描出表中各组数值所对应的点 ,并画出函数 关于 的图象; (3)、探究性质:随着自变量 的不断增大,函数 的变化趋势;(4)、解决问题:当 时, 的长度大约是 .(结果保留两位小数)15. 利用函数图象探究方程x|x-2|=的实数根的个数.
(3)、探究性质:随着自变量 的不断增大,函数 的变化趋势;(4)、解决问题:当 时, 的长度大约是 .(结果保留两位小数)15. 利用函数图象探究方程x|x-2|=的实数根的个数.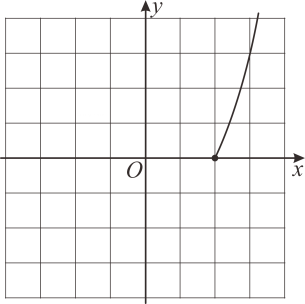 (1)、设函数y=x|x-2|,则这个函数的图象与直线y=的交点的坐标(填横或纵)就是方程x|x-2|=的实数根.(2)、分类讨论:当x<2时,y=-x2+2x;当x≥2时,y= .(3)、在给定的坐标系中,已经画出了当x≥2时的函数图象,请根据(2)中的解析式,通过描点,连线,画出当x<2时的函数图象.(4)、在给定的坐标系中画直线y= , 观察图象可知方程x|x-2|=的实数根有个.(5)、深入探究:若关于x的方程2x|x-2|=m有3个实数根,则m的取值范围是16. 在函数的学习过程中,我们经历“画函数图象一利用函数图象研究其性质一运用函数图象解决问题”的学习过程.
(1)、设函数y=x|x-2|,则这个函数的图象与直线y=的交点的坐标(填横或纵)就是方程x|x-2|=的实数根.(2)、分类讨论:当x<2时,y=-x2+2x;当x≥2时,y= .(3)、在给定的坐标系中,已经画出了当x≥2时的函数图象,请根据(2)中的解析式,通过描点,连线,画出当x<2时的函数图象.(4)、在给定的坐标系中画直线y= , 观察图象可知方程x|x-2|=的实数根有个.(5)、深入探究:若关于x的方程2x|x-2|=m有3个实数根,则m的取值范围是16. 在函数的学习过程中,我们经历“画函数图象一利用函数图象研究其性质一运用函数图象解决问题”的学习过程.下面根据学习函数的过程和方法,探究分段函数的相关性质和应用.
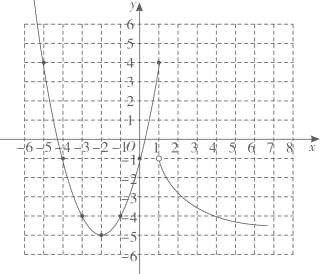 (1)、在如图所示的平面直角坐标系中,画出了分段函数图象的一部分,补全该分段函数的图象.
(1)、在如图所示的平面直角坐标系中,画出了分段函数图象的一部分,补全该分段函数的图象.写出该分段函数的一条性质:;
(2)、直线与该分段函数的图象有个交点,则的取值范围是;(3)、若该分段函数图象上有两点 , 且 , 则的取值范围是;(4)、当时,函数值的取值范围为 , 当取某个范围内的任意值时,为定值,直接写出满足条件的的取值范围及其对应的值.17. 如图1 ,在菱形 中, ,连结 .设 , 小宁根据学习函数的经验,对变量 与 之间的关系进行了如下探究.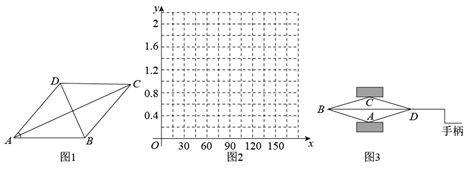 (1)、【探究】列表:通过观察补全下表(精确到 0.01).
(1)、【探究】列表:通过观察补全下表(精确到 0.01).15
30
45
60
75
90
105
120
135
150
165
1.72
1.08
0.37
0
0.73
1.08
1.41
1.72
描点、连线:在图2中描出表中各组数值所对应的点 ,并画出 关于 的函数图象.
(2)、【发现】结合画出的函数图象,写出该函数的两条性质:①;
② .
(3)、【应用】有一种 “千斤顶”,它是由4根长为 的连杆组成的菱形 ,当手柄顺时针旋转时, 两点的距离变小(如图 3).在这个过程中,当 时, 的度数约为 . (精确到1°).18. 如图,在 中, , 厘米, 厘米,点P从点B出发,沿 以每秒1厘米的速度匀速运动到点A . 设点P的运动时间为x秒,B、P两点间的距离为y厘米.小新根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小新的探究过程,请补充完整: (1)、通过取点、画图、测量,得到了x与y的几组值,如下表:
(1)、通过取点、画图、测量,得到了x与y的几组值,如下表:x(s)
0
1
2
3
4
5
6
7
y( )
0
1.0
2.0
3.0
2.7
2.7
m
3.6
m的值是 .
(2)、建立平面直角坐标系,描出表格中所有各对对应值为坐标的点,画出该函数的图象; (3)、结合画出的函数图象,解决问题:在曲线部分的最低点时,在 中画出点P所在的位置,此时P运动的时间为 ▲ 秒19. 如图,在△ABC中,∠C=90°,BC=6cm,AC=8cm,点D是AB的中点,以D为顶点作∠MDN=∠A,∠MDN的两边分别与线段AC交于点M.N(点M在点N左边).设A,M两点间的距离为xcm,C、N两点间的距离为ycm.
(3)、结合画出的函数图象,解决问题:在曲线部分的最低点时,在 中画出点P所在的位置,此时P运动的时间为 ▲ 秒19. 如图,在△ABC中,∠C=90°,BC=6cm,AC=8cm,点D是AB的中点,以D为顶点作∠MDN=∠A,∠MDN的两边分别与线段AC交于点M.N(点M在点N左边).设A,M两点间的距离为xcm,C、N两点间的距离为ycm.小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整.
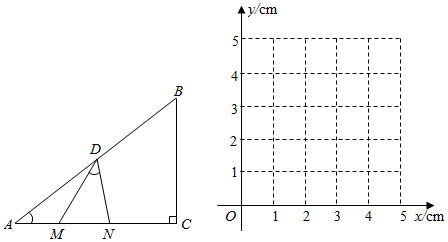 (1)、列表:下表的已知数据是根据A,M两点间的距离x进行取点、画图、测量,分别得到了x与y的几组对应值:
(1)、列表:下表的已知数据是根据A,M两点间的距离x进行取点、画图、测量,分别得到了x与y的几组对应值:x/cm
0
0.6
1.2
1.8
2.3
2.9
3.4
3.5
4.0
4.3
4.5
4.7
4.8
y/cm
a
4.6
4.3
3.9
3.6
3.1
2.6
2.4
b
1.2
0.9
0.4
0.2
请你补全表格:a=;b=.
(2)、描点、连线:在平面直角坐标系xOy中,描出表中各组数值所对应的点(x,y),并画出函数y关于x的图象:(3)、探究性质:随着自变量x的不断增大,函数y的变化趋势:.(4)、解决问题:当AM=CN时,A、M两点间的距离大约是cm.(保留一位小数)20. 某数学小组对函数y1= 图象和性质进行探究.当x=4时,y1=0. (1)、当x=5时,求y1的值;(2)、在给出的平面直角坐标系中,补全这个函数的图象,并写出这个函数的一条性质;(3)、进一步探究函数图象并解决问题:已知函数y2=﹣ 的图象如图所示,结合函数y1的图象,直接写出不等式y1≥y2的解集.21. 有这样一个问题:探究函数 的图象与性质.小美根据学习函数的经验,对函数 的图象与性质进行了探究.下面是小美的探究过程,请补充完整:(1)、函数 的自变量 的取值范围是 .(2)、下表是 与 的几组对应值.
(1)、当x=5时,求y1的值;(2)、在给出的平面直角坐标系中,补全这个函数的图象,并写出这个函数的一条性质;(3)、进一步探究函数图象并解决问题:已知函数y2=﹣ 的图象如图所示,结合函数y1的图象,直接写出不等式y1≥y2的解集.21. 有这样一个问题:探究函数 的图象与性质.小美根据学习函数的经验,对函数 的图象与性质进行了探究.下面是小美的探究过程,请补充完整:(1)、函数 的自变量 的取值范围是 .(2)、下表是 与 的几组对应值.如图,在平面直角坐标系 中,描出以上表中各对对应值为坐标的点.
根据描出的点,画出该函数的图象,标出函数的解析式.
 (3)、结合函数的图象,写出该函数的一条性质: .22. 探究与应用
(3)、结合函数的图象,写出该函数的一条性质: .22. 探究与应用【探究发现】
某数学小组的同学在学习完函数及一次函数后,掌握了函数的探究路径,即:定义→图像→性质→应用,他们尝试沿着此路径探究下列情景问题:
点A是数轴上一点,表示的数是2;点B是数轴上一动点,若它表示的数是x , 的距离为 . 随着x的变化,的距离y会如何变化呢?
 (1)、数学小组通过列表得到以下数据:
(1)、数学小组通过列表得到以下数据:0
1
2
3
4
5
4
m
2
1
0
1
2
3
其中m= .
数学小组发现给定一个x的值,就会有唯一的一个y值与之对应,y是x的函数吗?(填“是”或“不是”);
(2)、请通过描点、连线画出该函数图象,并根据函数图象写出该函数的一条性质: ▲ ; (3)、【应用拓展】
(3)、【应用拓展】若点 , 均在该函数图象上,请直接写出a , b满足的数量关系:;
(4)、将该函数图象在直线上方的部分保持不变,下方的图象沿直线进行翻折,得到新函数图象,若一次函数与该函数图象只有一个交点,则k的取值范围为 .(备注:直线y=2即过点且与x轴平行的直线.)
23. 已知 均是x的函数,下表是 与 的几组对应值.
小聪根据学习函数的经验,利用上述表格所反映出的 与x之间的变化规律,分别对函数 的图象与性质进行了探究.
下面是小聪的探究过程,请补充完整:
(1)、如图,在同一平面直角坐标系 中,描出上表中各组数值所对应的点 ,并画出函数 的图象;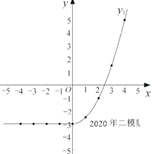 (2)、结合画出的函数图象,解决问题:
(2)、结合画出的函数图象,解决问题:①当 时,对应的函数值 约为;
②写出函数 的一条性质:;
③当 时, 的取值范围是 .
24. 小星在学习中遇到这样一个问题:如图1 中, , , ,点 在线段 上,且 ,点 是线段 上一动点,连接 ,以 为圆心、 的长为半径画弧交线段 于点 ,连接 ,当 是 中某条边的 倍时,求 的长.小星的探究过程如下:
⑴小星分析发现,有三种可能存在的情况,其中,当 时,通过推理计算可得 的长为 .但当他进一步研究其余两种情况时,发现很难通过常规的推理计算得到 的长,于是尝试利用学习函数的经验解决问题.
⑵小星将线段 的长度记为 , 和 的长度分别记为 , ,并分别对函数 , 随着自变量 的变化规律进行探究.小星通过取点、画图、测量,得到了下表中的几组对应值:
①在探究过程中,小星发现当 时,无须测量可以求出 的长,此时 的长约为 (结果精确到 .参考数据: ).
②利用表格中的数据,小星已经在图2所示的平面直角坐标系中画出了 关于 的函数图象,请你根据上文中 和 的 组对应值在此平面直角坐标系中描点,并画出 关于 的函数图象
⑶小星发现,想用函数图象彻底解决这个问题,还需要在平面直角坐标系内再画出一个函数的图象,请直接写出这个函数的解析式: , 并在上述平面直角坐标系中画出该函数的图象.
⑷请结合图象直接写出:当 是 或 的 倍时, 的长约为(结果精确到 ).
25. 如图,在 中, 是 的中点, 是边 上一动点,连结 ,取 的中点 ,连结 .小梦根据学习函数的经验,对 的面积与 的长度之间的关系进行了探究: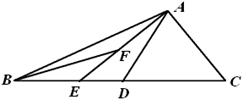 (1)、设 的长度为 , 的面积 ,通过取 边上的不同位置的点 ,经分析和计算,得到了 与 的几组值,如下表:
(1)、设 的长度为 , 的面积 ,通过取 边上的不同位置的点 ,经分析和计算,得到了 与 的几组值,如下表:0
1
2
3
4
5
6
3
1
0
2
3
根据上表可知, , .
(2)、在平面直角坐标系 中,画出(1)中所确定的函数的图象. (3)、在(1)的条件下,令 的面积为 .
(3)、在(1)的条件下,令 的面积为 .①用 的代数式表示 .
②结合函数图象.解决问题:当 时, 的取值范围为.
26. 小颖根据学习函数的经验,对函数的图像与性质进行了探究下面是小颖的探究过程,请你补充完整 (1)、列表:
(1)、列表:① ;
②若 , 为该函数图象上不同的两点,则 ;
(2)、描点并画出该函数的图象;(3)、①根据函数图象可得:该函数的最大值为 ;②写出函数图象的两条性质: ;
③若方程有两个实数解,求的取值范围: ;
④当时的取值范围是 ;
⑤将沿轴至少平移 个单位长度,能使与的函数图象无交点?
27. 如图,在中,点D是边的中点,点E是边上的一个动点,连接 . 设的面积为y,的长为x,小明对变量x和y之间的关系进行了探究,得到了如下的数据:请根据以上信息,解答下列问题:

x
0
3
6
y
3
0
3
(1)、题中的自变量和因变量分别是什么?当时,y的值是多少?直接写出的值;(2)、当的面积为面积的时,求出x的值.28. 八年级下册,我们曾经探究过“一元一次方程、一元一次不等式与一次函数”之间的关系,学会了运用一次函数的图象可以解一元一次方程与一元一次不等式.例如:一次函数y=3x+2与x轴交点的横坐标是方程3x+2=0的解;一次函数y=3x+2在x轴上方部分图像的自变量取值范围是不等式3x+2>0的解集.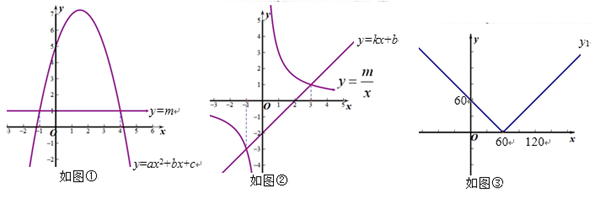
 (1)、【类比解决】
(1)、【类比解决】利用图像解下列方程或不等式.
Ⅰ.如图①,方程ax2+bx+c-m=0的解为;
Ⅱ.如图②,不等式kx+b< 的解为 .
(2)、【拓展探究】已知函数y1=|60-x|,y2=|120-x|.
Ⅰ.利用分类思想,可将函数y1=|60-x|先转化为 ,然后分别画出y1=60-x的图像x≤60的部分和y1=x-60的图像x>60的部分,就可以得到函数y1=|60-x|的图像,如图③所示.请在图③所在的平面直角坐标系中直接画出y2=|120-x|的图像.
Ⅱ.已知min{m,n} =m(m≤n),例如:min{1,-2} =-2.若y=min{y1 , y2}的图像为W,请计算图像W与坐标轴围成图形的总面积.
(3)、【实际应用】有一条长为600米的步行道OA,A是垃圾投放点w1,若以O为原点,OA为x轴正半轴建立直角坐标系,设B(x,0),现要在步行道上建另一座垃圾投放点w2(t,0),点B与w1的距离为d1=|600-x|,点B与w2的距离为d2=|x-t|,d表示与B点距离最近的垃圾投放点的距离,即:d=min{d1,d2}.若可以通过函数d的图像与坐标轴围成的总面积来测算扔垃圾的便利程度,面积越小越便利.问:垃圾投放点w2建在何处才能比建在OA中点时更加便利?
29. 若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数,下面我们参照学习函数的过程与方法,探究分段函数y= 的图象与性质,探究过程如下,请补充完整.(1)、列表:x
…
-4
-3
-2
-1
0
1
2
3
4
…
y
…
3
m
1
0
1
2
1
n
…
其中,m= , n=.
(2)、描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示,请画出函数的图象.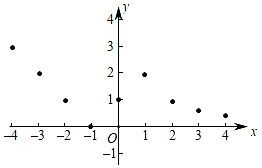 (3)、研究函数并结合图象与表格,回答下列问题:
(3)、研究函数并结合图象与表格,回答下列问题:①点A( ,y1),B(5,y2),C(x1 , ),D(x2 , 6)在函数图象上,则y1 ▲ y2 , x1 ▲ x2;(填“>”,“=”或“<”)
②当函数值y=1时,求自变量x的值;
(4)、若直线y=﹣x+b与函数图象有且只有一个交点,请直接写出b的取值范围.30. 小亮在学习中遇到如下一个问题:如图1,点 是半圆 上一动点,线段AB=6,CD平分 ,过点 作 交 于点 ,连接 .当 为等腰三角形时,求线段 的长度.
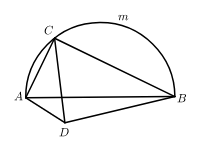
小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是他尝试结合学习函数的经验研究此问题.将线段 的长度作为自变量 , , 和 的长度都是 的函数,分别记为 , 和 .请将下面的探究过程补充完整:
(1)、根据点 在半圆 上的不同位置,画出相应的图形,测量线段 , , 的长度,得到下表的几组对应值:0
1.0
2.0
3.0
4.0
4.5
5.0
5.5
6
6
5.9
5.7
5.2
4.5
a
3.3
2.4
0
6
5.0
4.2
3.7
4
4.5
5.3
6.3
8.5
①上表中 的值是 ▲
②操作中发现,“无需测量线段 的长度即可得到 关于 的函数解析式”.请直接写出 关于 的函数解析式.
(2)、小亮已在平面直角坐标系 中画出了函数 的图象,如图2所示.
①请在同一个坐标系中画出函数 和 的图象;
②结合图象直接写出当 为等腰三角形时,线段 长度的近似值(结果保留一位小数).
-