备考2024年中考数学探究性训练专题15 二次函数
试卷更新日期:2024-03-24 类型:二轮复习
一、选择题
-
1. 我们在探究二次函数的图象与性质时,首先从y=ax2(a≠0)的形式开始研究,最后到y=a(x-h)2+k(a≠0)的形式,这种探究问题的思路体现的数学思想是( )A、转化 B、由特殊到一般 C、分类讨论 D、数形结合2. 如图,抛物线与x轴相交于点 , , 与y轴相交于点C,甲、乙、丙、丁四名同学在一起探究该函数的图象与性质,下面是他们得出的结论,其中正确的个数是( )
 A、1 B、2 C、3 D、43. 在数学活动课上,王老师出示一道数学题目:“在平面直角坐标系 中,当 为何值时,抛物线 与直线段 有唯一公共点或有两个公共点?”某学习小组经探究得到以下四个结论:
A、1 B、2 C、3 D、43. 在数学活动课上,王老师出示一道数学题目:“在平面直角坐标系 中,当 为何值时,抛物线 与直线段 有唯一公共点或有两个公共点?”某学习小组经探究得到以下四个结论:①当 时,有唯一公共点;②若 为整数,则仅当 的值为4或5或6或7时,才有唯一公共点;③若 为整数,则当 的值为1或2或3时,有两个公共点;④当 时,有两个公共点.其中正确的结论有( )
A、①②④ B、①②③ C、①③ D、①④4. 已知在平面直角坐标系xOy中,点A的坐标为(3,4),M是抛物线(a≠0)对称轴上的一个动点,小明经探究发现:当的值确定时,抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定.当满足( )时,抛物线(a≠0)的对称轴上存在4个不同的点M,使△AOM为直角三角形.A、 B、 C、 D、二、填空题
-
5. 某学习小组为了探究函数y=x2﹣|x|的图象和性质,根据以往学习函数的经验,列表确定了该函数图象上一些点的坐标,表格中的m= .
x
…
﹣2
﹣1.5
﹣1
﹣0.5
0
0.5
1
1.5
2
…
y
…
2
0.75
0
﹣0.25
0
﹣0.25
0
m
2
…
6. 如图,已知A,B,C是函数y=x2图象上的动点,且三点的横坐标依次为a+1,a,a-1.小华用软件GeoGebra对△ABC的几何特征进行了探究,发现△ABC的面积是个定值,则这个定值为.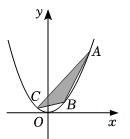 7. 已知在平面直角坐标系xOy中,点A的坐标为(3,4),M是抛物线 ( )对称轴上的一个动点。小明经探究发现:当 的值确定时,抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定。若抛物线 ( )的对称轴上存在3个不同的点M,使△AOM为直角三角形,则 的值是8. 如图,在平面直角坐标系xOy中,已知抛物线 y=-x(x-3)(0≤x≤3) 在x轴上方部分记作C1 , 它与x轴交于点O,A1 , 将C1绕点A1旋转180°得C2 , C2与x 轴交于另一点A2 . 继续操作并探究:将C2绕点A2旋转180°得C3 , 与x 轴交于另一点A3;将C3绕点A 2旋转180°得C4 , 与x 轴交于另一点A4 , 这样依次得到x轴上的点A1 , A2 , A3 , …,An , …,及抛物线C1 , C2 , …,Cn , ….则点A4的坐标为;Cn的顶点坐标为(n为正整数,用含n的代数式表示) .
7. 已知在平面直角坐标系xOy中,点A的坐标为(3,4),M是抛物线 ( )对称轴上的一个动点。小明经探究发现:当 的值确定时,抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定。若抛物线 ( )的对称轴上存在3个不同的点M,使△AOM为直角三角形,则 的值是8. 如图,在平面直角坐标系xOy中,已知抛物线 y=-x(x-3)(0≤x≤3) 在x轴上方部分记作C1 , 它与x轴交于点O,A1 , 将C1绕点A1旋转180°得C2 , C2与x 轴交于另一点A2 . 继续操作并探究:将C2绕点A2旋转180°得C3 , 与x 轴交于另一点A3;将C3绕点A 2旋转180°得C4 , 与x 轴交于另一点A4 , 这样依次得到x轴上的点A1 , A2 , A3 , …,An , …,及抛物线C1 , C2 , …,Cn , ….则点A4的坐标为;Cn的顶点坐标为(n为正整数,用含n的代数式表示) .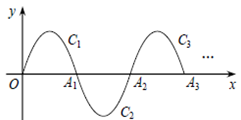
三、理论探究题
-
9. 我们定义:若点P在一次函数y=ax+b(a≠0)图象上,点Q在反比例函数图象上,且满足点P与点Q关于y轴对称,则称二次函数y=ax2+bx+c为一次函数y=ax+b与反比例函数的“衍生函数”,点P称为“基点”,点Q称为“靶点”.(1)、若二次函数y=2x2+6x+8是一次函数y=ax+b与反比例函数的“衍生函数”,则a= , b= , c= .(2)、直接写出一次函数y=x+b和反比例函数的“衍生函数”的表达式,若该“衍生函数”的顶点在x轴上,且“基点”P的横坐标为4,求出“靶点”Q的坐标;(3)、若一次函数y=ax+b(a>b>0)和反比例函数的“衍生函数”经过点(2,5).试判断一次函数y=ax+b图象上“基点”的个数,并说明理由;10. 配方法是数学中重要的一种思想方法,利用配方法可求一元二次方程的根,也可以求二次函数的顶点坐标等,所谓配方法是指将一个式子的某部分通过恒等变形化为完全平方式或几个完全平方式的和的方法,其实这种方法还经常被用到代数式的变形中,并结合非负数的意义解决某些问题.我们规定:一个整数能表示成 (a , b是整数)的形式,则称这个数为“完美数”.例如,5是“完美数”,理由:因为 , 所以5是“完美数”.(1)、【解决问题】:
下列各数中,“完美数”有 (只填序号);
①10 ②24 ③34 ④60
(2)、【探究问题】:若可配方成 (m , n为常数),则的值为;
(3)、已知 (a , b是整数,k是常数),要使S为“完美数”,试求出符合条件的一个k值,并说明理由;(4)、【拓展应用】:已知实数x , y均满足 , 求代数式的最小值.
11. 定义:若一个函数图象上存在纵坐标与横坐标互为相反数的点,则称该点为这个函数图象的“互逆点”
(1)、若点M(-2,m)是一次函数y=kx+6的图象上的“互逆点”,则k=若点N(n , -n)是函数y的图象上的“互逆点”,则n=
(2)、若点P(p , 3)是二次函数y=x2+bx+c的图象上唯一的“互逆点”,求这个二次函数的表达式;
(3)、若二次函数y=ax2+bx+c(a , b是常数,a>0)的图象过点(0,2),且图象上存在两个不同的“互逆点”A(x1 , -x1),B(x2 , -x2),且满足-1<x1<1,|x1x2|=2,如果z=b2+2b+2,请求出z的取值范围。
四、数形结合探究题
-
12. 有这样一个问题:探究函数的图象与性质.
嘉瑶根据学习函数的经验,对函数的图象与性质进行了探究.
下面是嘉瑶的探究过程,请补充完整:(1)、函数的图象与轴 交点;填写“有”或“无”(2)、下表是与的几组对应值:x … -3 -2 -1 - 1 2 … y … -2 - n … 则的值为 ;
(3)、如图,在平面直角坐标系中,嘉瑶描出各对对应值为坐标的点请你根据描出的点,帮助嘉瑶画出该函数的大致图象; (4)、请你根据探究二次函数与一元二次方程关系的经验,结合图象直接写出方程的根约为结果精确到13. 某数学兴趣小组对函数 的图象和性质进行了研究,探究过程如下.
(4)、请你根据探究二次函数与一元二次方程关系的经验,结合图象直接写出方程的根约为结果精确到13. 某数学兴趣小组对函数 的图象和性质进行了研究,探究过程如下.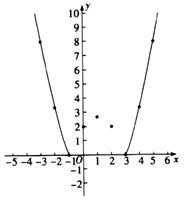 (1)、自变量x的取值范围是全体实数,x与y的几组对应值列表如下.
(1)、自变量x的取值范围是全体实数,x与y的几组对应值列表如下.x
…
-3
-2
-1
0
1
2
3
4
5
…
y
…
8
m
0
2
n
2
0
8
…
其中,m= , n=;
(2)、根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请补全函数图象的剩余部分;(3)、进一步探究函数图象发现:①函数图象与x轴有个交点;
②方程 有个实数根;
③当关于x的方程 有3个实数根时,p的值是.
14.(1)、【问题初探】综合与实践数学活动课上,张老师给出了一个问题:
已知二次函数y=x2+2x-3,当-2≤x≤2时,y的取值范围为;
①小伟同学经过分析后,将原二次函数配方成y=a(x-h)2+k
形式,确定抛物线对称轴为直线x=h , 通过-2、h和2的大小
关系,分别确定了最大值和最小值,进而求出y的取值范围;
②小军同学画出如图的函数图象,通过观察图象确定了y的取值范围;请你根据上述两名同学的分析写出y的取值范围是;
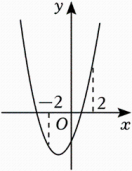 (2)、【类比分析】
(2)、【类比分析】张老师发现两名同学分别从“数”和“形”的角度分析、解决问题,为了让同学们更好感悟“数形结合”思想,张老师将前面问题变式为下面问题,请你解答:已知二次函数y=-x2+2x-3,当-2≤x≤2时,求y的取值范围;
(3)、【学以致用】已知二次函数y=-x2+6x-5,当a≤x≤a+3时,二次函数的最大值为y1 , 最小值为y2 , 若y1-y2=3,求a的值.
15. 小明为了探究函数M:的性质,他想先画出它的图象,然后再观察、归纳得到,并运用性质解决问题.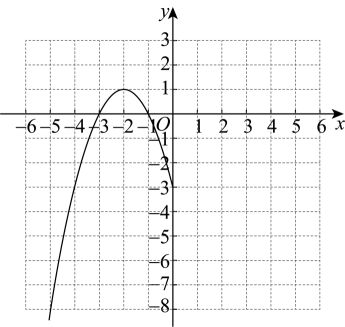 (1)、完成函数图象的作图,并完成填空.
(1)、完成函数图象的作图,并完成填空.①列出y与x的几组对应值如下表:
x
…
-5
-4
-3
-2
-1
0
1
2
3
4
5
…
y
…
-8
-3
0
1
0
-3
0
1
0
a
-8
…
表格中,a= ▲ ;
②结合上表,在下图所示的平面直角坐标系xOy中,画出当x>0时函数M的图象;
③观察图象,当x= ▲ 时,y有最大值为 ▲ ;
(2)、求函数M:与直线l:的交点坐标;(3)、已知P(m,),Q(m+1,)两点在函数M的图象上,当时,请直接写出m的取值范围.16. 根据学习函数的经验,探究函数 (b<0)的图象和性质: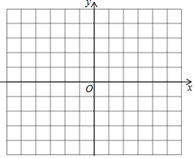 (1)、下表给出了部分x,y的取值;
(1)、下表给出了部分x,y的取值;x
…
﹣3
﹣2
﹣1
0
1
2
3
4
5
…
y
…
3
0
﹣1
0
3
0
﹣1
0
3
…
由上表可知,a= , b=;
(2)、用你喜欢的方式在坐标系中画出函数y=x2+ax﹣4|x+b|+4的图象;(3)、若方程x2+ax﹣4|x+b|+4=x+m至少有3个不同的实数解,请直接写出m的取值范围.17. 有这样一个问题:探究函数y= (x-1)(x-2)(x-3)+x的性质. (1)、先从简单情况开始探究:
(1)、先从简单情况开始探究:①当函数y= (x-1)+x时,y随x增大而(填“增大”或“减小”);
②当函数y= (x-1)(x-2)+x时,它的图象与直线y=x的交点坐标为;
(2)、当函数y= (x-1)(x-2)(x-3)+x时,下表为其y与x的几组对应值.x
…
-
0
1
2
3
4
…
y
…
-
-3
1
2
3
7
…
①如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象;
②根据画出的函数图象,写出该函数的一条性质: ▲ 。
18. 如图,将一三角板放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B , 另一边与射线DC相交于Q.探究:设A、P两点间的距离为x.
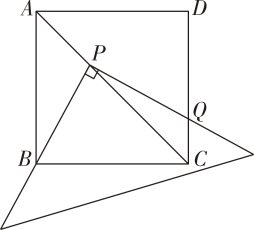 (1)、当点Q在边CD上时,线段PQ与PB之间有怎样的数量关系?试证明你的猜想;(2)、当点Q在边CD上时,设四边形PBCQ的面积为y , 求y与x之间的函数关系,并写出函数自变量x的取值范围;(3)、当点P在线段AC上滑动时,是否可能成为等腰三角形?如果可能,指出所有能使成为等腰三角形的点Q的位置.并写出相应的x值,如果不可能,试说明理由.19. 综合与探究:
(1)、当点Q在边CD上时,线段PQ与PB之间有怎样的数量关系?试证明你的猜想;(2)、当点Q在边CD上时,设四边形PBCQ的面积为y , 求y与x之间的函数关系,并写出函数自变量x的取值范围;(3)、当点P在线段AC上滑动时,是否可能成为等腰三角形?如果可能,指出所有能使成为等腰三角形的点Q的位置.并写出相应的x值,如果不可能,试说明理由.19. 综合与探究:如图,抛物线经过坐标轴上三点,直线过点和点 .
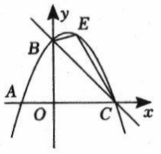 (1)、求抛物线的解析式;(2)、是直线上方抛物线上一动点,连接 , 求面积的最大值及此时点的坐标;(3)、是抛物线对称轴上的动点,在抛物线上是否存在点 , 使得以为顶点的四边形是平行四边形?若存在,请直接写出所有满足条形的点坐标;若不存在,请说明理由.20. 有这样一个问题:探究函数的图象与性质.思宇根据学习函数的经验,对函数的图象与性质进行了探究.下面是思宇的探究过程,请补充完整:
(1)、求抛物线的解析式;(2)、是直线上方抛物线上一动点,连接 , 求面积的最大值及此时点的坐标;(3)、是抛物线对称轴上的动点,在抛物线上是否存在点 , 使得以为顶点的四边形是平行四边形?若存在,请直接写出所有满足条形的点坐标;若不存在,请说明理由.20. 有这样一个问题:探究函数的图象与性质.思宇根据学习函数的经验,对函数的图象与性质进行了探究.下面是思宇的探究过程,请补充完整: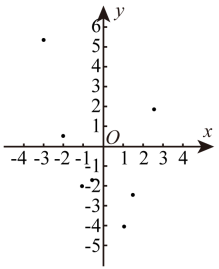 (1)、函数的图象与轴交点;(填写“有”或“无”)(2)、下表是与的几组对应值:
(1)、函数的图象与轴交点;(填写“有”或“无”)(2)、下表是与的几组对应值:…
1
2
…
…
…
则的值为;
(3)、如图,在平面直角坐标系中,思宇描出各对对应值为坐标的点.请你根据描出的点,帮助思宇画出该函数的大致图象;(4)、结合函数的图象,写出该函数的其他性质(一条即可): .21. 二次函数的图象交轴于原点及点 . (1)、感知特例:
(1)、感知特例:当时,如图1,抛物线上的点 , , , , 分别关于点中心对称的点为 , , , , , 如下表:
…
( ▲ , ▲)
…
…
…
①补全表格:A ( ▲ , ▲)
②请在图1中描出表中对称后的点,再用平滑的曲线依次连接各点,得到的图象记为 .
(2)、形成概念:
我们发现形如(1)中的图象上的点和抛物线上的点关于点中心对称,则称是的“孔像抛物线”.例如,当时,图2中的抛物线是抛物线的“孔像抛物线”.
探究问题①当时,若抛物线与它的“孔像抛物线”的函数值都随着的增大而减小,则的取值范围为 ▲;
②若二次函数及它的“孔像抛物线”与直线有且只有三个交点,求的值.
22. 综合运用如图,在平面直角坐标系中,已知抛物线与轴交于、两点,与轴交于点 , 连接 .
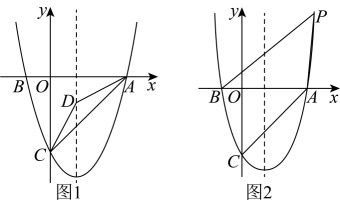 (1)、求抛物线的解析式与顶点坐标;(2)、如图1,在对称轴上是否存在一点 , 使 , 若存在,请求出点的坐标;若不存在,请说明理由;(3)、如图2,若点是抛物线上的一个动点,且 , 请直接写出点的横坐标.
(1)、求抛物线的解析式与顶点坐标;(2)、如图1,在对称轴上是否存在一点 , 使 , 若存在,请求出点的坐标;若不存在,请说明理由;(3)、如图2,若点是抛物线上的一个动点,且 , 请直接写出点的横坐标.五、实践探究题
-
23. 深圳市某景观公园计划修建一个人工喷泉,从垂直于地面的喷水枪喷出的水流路径可以看作是抛物线的一部分.记喷出的水流距喷水枪的水平距离为x米,距地面的竖直高度为y米,获得数据如表:
x(米)
0
0.5
2
3.5
5
y(米)
2.25
3
2.25
0
小华根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小华的探究过程,请补充完整:
 (1)、在平面直角坐标系xOy中,描出以表中各组对应值为坐标的点,并用平滑曲线画出该函数的图象;(2)、直接写出水流最高点距离地面的高度为 米;(3)、求该抛物线的表达式;(结果用一般式表示)(4)、结合函数图象,解决问题:该景观公园准备在距喷水枪水平距离3米处修建一个大理石雕塑,使喷水枪喷出的水流刚好落在雕塑顶端,则大理石雕塑的高度约为 米.(结果精确到0.1米)24. 在一条笔直的滑道上有黑、白两个小球同向运动,黑球在A处开始减速,此时白球在黑球前面70cm处.
(1)、在平面直角坐标系xOy中,描出以表中各组对应值为坐标的点,并用平滑曲线画出该函数的图象;(2)、直接写出水流最高点距离地面的高度为 米;(3)、求该抛物线的表达式;(结果用一般式表示)(4)、结合函数图象,解决问题:该景观公园准备在距喷水枪水平距离3米处修建一个大理石雕塑,使喷水枪喷出的水流刚好落在雕塑顶端,则大理石雕塑的高度约为 米.(结果精确到0.1米)24. 在一条笔直的滑道上有黑、白两个小球同向运动,黑球在A处开始减速,此时白球在黑球前面70cm处.
小聪测量黑球减速后的运动速度(单位:cm/s)、运动距离(单位:cm)随运动时间(单位:S)变化的数据,整理得下表.
运动时间t/s
0
1
2
3
4
运动速度y/cm/s
10
9.5
9
8.5
8
运动距离y/cm
0
9.75
19
27.7
36
小聪探究发现,黑球的运动速度v与运动时间t之间成一次函数关系,运动距离y与运动时间t之间成二次函数关系.
(1)、直接写出v关于t的函数解析式和y关于t的函数解析式(不要求写出自变量的取值范围)(2)、当黑球减速后运动距离为64cm时,求它此时的运动速度;(3)、若白球一直以2cm/s的速度匀速运动,问黑球在运动过程中会不会碰到白球?请说明理由.25. 根据以下素材,探索完成任务.如何设计跳长绳方案
素材1
图1是集体跳长绳比赛,比赛时,各队跳绳10人,摇绳2人,共计12人图2是绳甩到最高处时的示意图,可以近似的看作一条抛物线,正在甩绳的甲、乙两位队员拿绳的手间距6米,到地面的距离均为1米,绳子最高点距离地面2.5米.
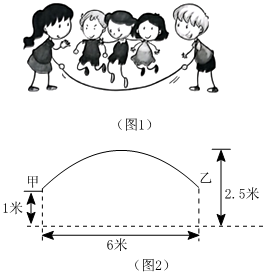
素材2
某队跳绳成员有6名男生和4名女生,男生身高1.70米至1.80米,女生身高1.66米至1.69米跳长绳比赛时,可以采用一路纵队或两路纵队并排的方式安排队员位置,但为了保证安全,人与人之间距离至少0.5米
问题解决
任务1
确定长绳形状
在图2中建立合适的直角坐标系,并求出抛物线的函数表达式
任务2
探究站队方式
当该队以一路纵队的方式跳绳时,绳子能否顺利的甩过所有队员的头顶?
任务3
拟定位置方案
为了更顺利的完成跳绳,现按中间高两边低的方式居中安排站位请在你所建立的坐标系中,求出左边第一位跳绳队员横坐标的最大取值范围.
26. 根据以下素材,探索完成任务.如何设计喷水装置的高度?
素材1
图1为某公园的圆形喷水池,图2是其示意图,O为水池中心,喷头A、B之间的距离为20米,喷射水柱呈抛物线形,水柱距水池中心处达到最高,高度为.水池中心处有一个圆柱形蓄水池,其底面直径为 , 高为1.8米.


素材2
如图3,拟在圆柱形蓄水池中心处建一喷水装置( , 并从点P向四周喷射与图2中形状相同的抛物线形水柱,且满足以下条件:
①水柱的最高点与点P的高度差为;
②不能碰到图2中的水柱;
③落水点G,M的间距满足:.
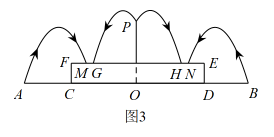
问题解决
任务1
确定水柱形状
在图2中以点O为坐标原点,水平方向为x轴建立直角坐标系,并求左边这条抛物线的函数表达式.
任务2
探究落水点位置
在建立的坐标系中,求落水点G的坐标.
任务3
拟定喷水装置的高度
求出喷水装置的高度.
27. 根据以下素材,探索完成任务.如何设计喷泉喷头的升降方案?
素材1
如图1,湖中有一个可垂直升降的喷泉,喷出的水柱呈抛物线.记水柱上某一点到喷头的水平距离为x米,到湖面的垂直高度为y米.当喷头位于起始位置时,测量得x与y的四组数据如下:
x(米)
0
2
3
4
y(米)
1
2
1.75
1

素材2
公园想设立新的游玩项目,通过升降喷头,使游船能从水柱下方通过,如图2,为避免游船被喷泉淋到,要求游船从水柱下方中间通过时,顶棚上任意一点到水柱的竖直距离均不小于0.5米.已知游船顶棚宽度为3米,顶棚到湖面的高度为2米.
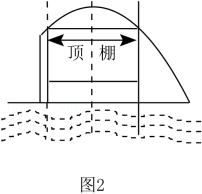
问题解决
任务1
确定喷泉形状
结合素材1,求y关于x的表达式.
任务2
探究喷头升降方案
为使游船按素材2要求顺利通过,求喷头距离湖面高度的最小值.
28.如何确定隧道中警示灯带的安装方案?
素材1
2022年10月,温州市府东路过江通道工程正式开工,建成后将成为温州瓯江第一条超大直径江底行车隧道。隧道顶部横截面可视为抛物线,如图1,隧道底部宽AB为10m,高OC为5m.


素材2
货车司机长时间在隧道内行车容易疲劳驾驶,为了安全,拟在隧道顶部安装上下长度为20cm的警示灯带,沿抛物线安装。(如图2).为了实效,相邻两条灯带的水平间距均为0.8m(灯带宽度可忽略);普通货车的高度大约为2.5m(载货后高度),货车顶部与警示灯带底部的距离应不少于50cm。灯带安装好后成轴对称分布.
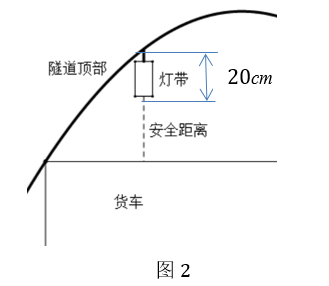
问题解决
任务1
确定隧道形状
在图1中建立合适的直角坐标系,求抛物线的函数表达式.
任务2
探究安装范围
在你建立的坐标系中,在安全的前提下,确定灯带安装点的横、纵坐标的取值范围.
任务3
拟定设计方案
求出同一个横截面下,最多能安装几条灯带,并根据你所建立的坐标系,求出最右边一条灯带安装点的横坐标.
29. 综合与应用如果将运动员的身体看作一点,则他在跳水过程中运动的轨迹可以看作为抛物线的一部分.建立如图2所示的平面直角坐标系xOy,运动员从点A(0,10)起跳,从起跳到入水的过程中,运动员的竖直高度y (m)与水平距离x (m)满足二次函数的关系.
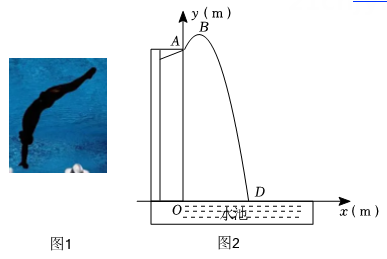 (1)、在平时的训练完成一次跳水动作时,运动员甲的水平距离x与竖直高度y的几组数据如下表:
(1)、在平时的训练完成一次跳水动作时,运动员甲的水平距离x与竖直高度y的几组数据如下表:水平距离x(m)
0 1
1.5
竖直高度y(m)
10
10
6.25
根据上述数据,求出y关于x的关系式;
(2)、在(1)的这次训练中,求运动员甲从起点A到入水点的水平距离OD的长;(3)、信息1:记运动员甲起跳后达到最高点B到水面的高度为k(m),从到达到最高点B开始计时,则他到水面的距离h (m)与时间t (s)之间满足h=-5t2+k .信息2:已知运动员甲在达到最高点后需要1.6s的时间才能完成极具难度的270C 动作.
问题解决:
①请通过计算说明,在(1)的这次训练中,运动员甲能否成功完成此动作?
②运动员甲进行第二次跳水训练,此时他的竖直高度y(m)与水平距离x (m)的关系为y =ax2-ax+10(a<0),若选手在达到最高点后要顺利完成270C 动作,则a的取值范围是 ▲ .
30. 【综合与实践】数学来源于生活,同时数学也可以服务于生活.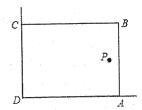
【知识背景】如图,校园中有两面直角围墙,墙角内的P处有一古棵树与墙 , 的距离分别是和 , 在美化校园的活动中,某数学兴趣小组想借助围墙(两边足够长),用长的篱笆围成一个矩形花园(篱笆只围 , 两边),设.
【方案设计】设计一个矩形花园,使之面积最大,且要将古棵树P围在花园内(含边界,不考虑树的粗细).
【解决问题】思路:把矩形的面积S与边长x(即的长)的函数解析式求出,并利用函数的性质来求面积的最大值即可.
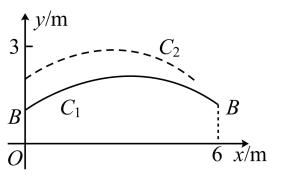
(1)、请用含有x的代数式表示的长;(2)、花园的面积能否为?若能,求出x的值,若不能,请说明理由;(3)、求面积S与x的函数解析式,写出x的取值范围;并求当x为何值时,花园面积S最大?31. 嘉嘉和淇淇在玩沙包游戏.某同学借此情境编制了一道数学题,请解答这道题.如图,在平面直角坐标系中,一个单位长度代表1m长.嘉嘉在点处将沙包(看成点)抛出,其运动路线为抛物线:的一部分,淇淇恰在点处接住,然后跳起将沙包回传,其运动路线为抛物线:一部分.
 (1)、写出的最高点坐标,并求a,c的值;(2)、若嘉嘉在x轴上方1m的高度上,且到点A水平距离不超过1m的范围内可以接到沙包,求符合条件的n的整数值.32. 某校想将新建图书楼的正门设计为一个抛物线型门,并要求所设计的拱门的跨度与拱高之积为48m2 , 还要兼顾美观、大方、和谐、通畅等因素,设计部门按要求给出了两个设计方案.现把这两个方案中的拱门图形放入平面直角坐标系中,如图所示:
(1)、写出的最高点坐标,并求a,c的值;(2)、若嘉嘉在x轴上方1m的高度上,且到点A水平距离不超过1m的范围内可以接到沙包,求符合条件的n的整数值.32. 某校想将新建图书楼的正门设计为一个抛物线型门,并要求所设计的拱门的跨度与拱高之积为48m2 , 还要兼顾美观、大方、和谐、通畅等因素,设计部门按要求给出了两个设计方案.现把这两个方案中的拱门图形放入平面直角坐标系中,如图所示: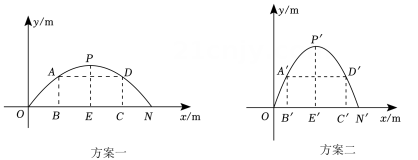
方案一:抛物线型拱门的跨度 , 拱高PE.其中,点在轴上,.方案二,抛物线型拱门的跨度 , 拱高.其中,点在轴上, , .
要在拱门中设置高为3m的矩形框架,其面积越大越好(框架的粗细忽略不计).方案一中,矩形框架ABCD的面积记为S1 , 点A,D在抛物线上,边BC在ON上;方案二中,矩形框架的面积记为S2 , 点 , 在拋物线上,边在上.现知,小华已求出方案二中,当时, , 请你根据以上信息,解答下列问题:
(1)、求方案一中掲物线的函数表达式.(2)、在方案一中,当时,求矩形框架ABCD的面积并比较的大小.33. 根据以下素材,探索完成任务.如何设计拱桥上救生圈的悬挂方案?
素材1
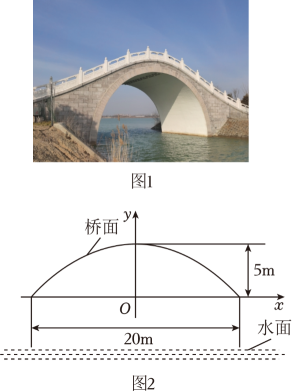
图1是一座抛物线形拱桥,以抛物线两个水平最低点连线为x轴,过抛物线离地面的最高点的铅垂线为y轴建立平面直角坐标系,某时测得水面宽20m , 拱顶离水面最大距离为10m , 抛物线拱形最高点与x轴的距离为5m . 据调查 , 该河段水位在此基础上再涨1m达到最高.
素材2
为方便救助溺水者,拟在图1的桥拱上方栏杆处悬挂救生圈,如图3,为了方便悬挂,救生圈悬挂点距离抛物线拱面上方1m,且相邻两救生圈悬挂点的水平间距为4m.为美观,放置后救生圈关于y轴成轴对称分布.(悬挂救生圈的柱子大小忽略不计) 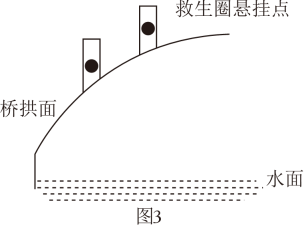
问题解决:
(1)、任务1:确定桥拱形状根据图2,求抛物线的函数表达式.
(2)、任务2:拟定设计方案求符合悬挂条件的救生圈个数,并求出最右侧一个救生圈悬挂点的坐标.
(3)、任务3:探究救生绳长度当水位达到最高时,上游一个落水者顺流而下到达抛物线拱形桥面的瞬间,若要确保救助者把拱桥上任何一处悬挂点的救生圈抛出都能抛到落水者身边,求救生绳至少需要多长.(救生圈大小忽略不计,结果保留整数.)
34. 某校准备在校园里利用围墙(墙可用最大长度为)和长的篱笆墙,围成Ⅰ、Ⅱ两块矩形开心农场.某数学兴趣小组设计了三种方案(除围墙外,实线部分为篱笆墙,且不浪费篱笆墙),请根据设计方案回答下列问题: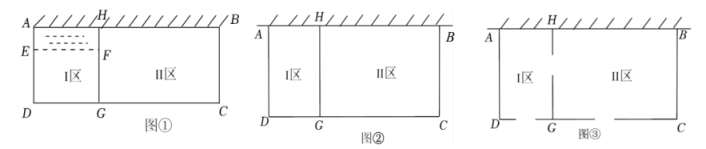 (1)、方案一:如图①,全部利用围墙的长度,但要在Ⅰ区中留一个宽度的矩形水池,且需保证总种植面积为 , 试确定的长;(2)、方案二:如图②,使围成的两块矩形总种植面积最大,请问应设计为多长?此时最大面积为多少?(3)、方案三:如图③,在图中所示三处位置各留宽的门,且使围成的两块矩形总种植面积最大,请问应设计为多长?此时最大面积为多少?35. 根据以下素材,探索完成任务.
(1)、方案一:如图①,全部利用围墙的长度,但要在Ⅰ区中留一个宽度的矩形水池,且需保证总种植面积为 , 试确定的长;(2)、方案二:如图②,使围成的两块矩形总种植面积最大,请问应设计为多长?此时最大面积为多少?(3)、方案三:如图③,在图中所示三处位置各留宽的门,且使围成的两块矩形总种植面积最大,请问应设计为多长?此时最大面积为多少?35. 根据以下素材,探索完成任务.绿化带灌溉车的操作方案
素材1
辆绿化带灌溉车正在作业,水从喷水口喷出,水流的上下两边缘可以抽象为两条抛物线的一部分:喷水口离开地面高1.6米,上边缘抛物线最高点离喷水口的水平距离为3米,高出|喷水口0.9米,下边缘水流形状与上边缘相同,且喷水口是最高点。

素材2
路边的绿化带宽4米
素材3
绿化带正中间种植了行道树,为了防治病虫害、增加行道树的成活率,园林工人给树木“打针”。针一般打在离地面1.5米到2米的高度(包含端点)。

问题解决
(1)、任务1:确定上边缘水流形状建立如图所示直角坐标系,求上边缘抛物线的函数表达式.
(2)、任务2:探究灌溉范围灌溉车行驶过程中喷出的水能浇浓到整个绿化带吗?请说明理由.
(3)、任务3:拟定设计方案灌溉时,发现水流的上下两边缘冲击力最强,喷到针筒容易造成针筒脱落。那么请问在满足最大灌溉面积的前提下对行道树“打针”是否有影响,并说明理由;若你认为有影响,请给出具体的“打针”范围。
36. 根据以下素材,探索完成任务.
素材1 图1为某公园的抛物线型拱桥,图2是其横截面示意图,测得水面宽度米,拱顶离水面的距离为米.
素材2 拟在公园里投放游船供游客乘坐,载重最少时,游船的横截面如图3所示,漏出水面的船身为矩形,船顶为等腰三角形.测得相关数据如下:米,米,米,米.
素材3 为确保安全,拟在石拱桥下面的P,Q两处设置航行警戒线,要求如下:
①游船底部在P,Q之间通行;
②当载重最少通过时,游船顶部E与拱桥的竖直距离至少为米.
(1)、任务1 确定拱桥形状:在图2中建立合适的直角坐标系,并求这条抛物线的函数表达式.(2)、任务2 设计警戒线之间的宽度:求的最大值.37. 根据以下素材,探究完成任务设计求碗中面汤面液宽度的方案 素材1 图1是一个瓷碗,图2是其截面图,碗体DEC呈抛物线状(碗体厚度不计),碗高GF=7cm,碗底宽AB=3cm,当瓷
碗中装满面汤时,液面宽CD= 12cm,此时面汤最大深度EG= 6cm,

素材2 如图3,把瓷碗绕点B缓缓倾斜倒出部分面汤,当点A离MN距离为1.8cm时停止.
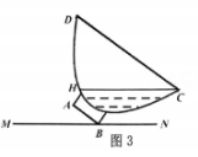
问题解决 任务1 确定碗体形状 在图2中建立合适的直角坐标系,求抛物线的函数表达式。
任务2 拟定设计方案1 根据图2位置,把碗中面汤喝掉一部分,当碗中液面高度(离桌面MN距离)为5cm时,求此时碗中液面宽度。
任务3 拟定设计方案2 如图3,当碗停止倾斜时,求此时碗中液面宽度CH,
38. 根据以下素材,探索完成任务.如何设计拱桥景观灯的悬挂方案?
素材1
图1中有一座拱桥,图2是其抛物线形桥拱的示意图,某时测得水面宽 , 拱顶离水面 . 据调查,该河段水位在此基础上再涨达到最高.
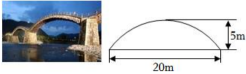
图1 图2
素材2
为迎佳节,拟在图1桥洞前面的桥拱上悬挂长的灯笼,如图3.为了安全,灯笼底部距离水面不小于;为了实效,相邻两盏灯笼悬挂点的水平间距均为;为了美观,要求在符合条件处都挂上灯笼,且挂满后成轴对称分布.
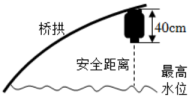
图3
问题解决
任务1
确定桥拱形状
在图2中建立合适的直角坐标系,求抛物线的函数表达式.
任务2
探究悬挂范围
在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围.
任务3
拟定设计方案(填空即可)
给出一种符合所有悬挂条件的灯笼数量,并根据你所建立的坐标系,求出最左边一盏灯笼悬挂点的横坐标.
39. 根据以下素材,探索完成任务.如何设计拱桥景观灯的悬挂方案?素材1
图1中有一座拱桥,图2是某抛物线形桥拱的示意图,某时测得水面宽20m,拱顶离水面5m.据调查,该河段水位在此基础上再涨1.8m达到最高.

素材2
为迎佳节,拟在图1桥沿前面的桥拱上悬挂40cm长的灯笼,如图3.为了安全,灯笼底部距离水面不小于1m;为了实效,相邻两盏灯笼悬挂点的水平间距均为1.6m;为了美观,要求在符合条件处都挂上灯笼,且挂满后成轴对称分布.

问题解决(1)、任务1确定桥拱形状
在图2中建立合适的直角坐标系,求抛物线的函数表达式.
(2)、任务2探究悬挂范围
在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围.
(3)、任务3拟定设计方案
给出一种符合所有悬挂条件的灯笼数量,并根据你所建立的坐标系,求出最左边一盏灯笼悬挂点的横坐标.
40. 阅读素材,完成任务.测试机器人行走路径
素材一
图1是某校科技兴趣小组设计的一个可以帮助餐厅上菜的机器人,该机器人能根据指令要求进行旋转和行走.如图为机器人所走的路径.机器人从起点出发,连续执行如下指令:机器人先向前直行(表示第次行走的路程),再逆时针旋转 , 直到第一次回到起点后停止.记机器人共行走的路程为 , 所走路径形成的封闭图形的面积为S .

素材二
如图2,当每次直行路程均为1(即),时,机器人的运动路径为 , 机器人共走的路程 , 由图2图3易得所走路径形成的封闭图形的面积为 .

素材三
如图4,若 , 机器人执行六次指令后回到起点处停止.
解决问题
任务
固定变量
探索变量
探索内容
任务一
直行路程
旋转角度与路程
任务二
旋转角度
直行路程
若 , 求与的值.
任务三
旋转角度 , 路程
路径形成的封闭图形面积S .
若 , 请直接写出与之间的数量关系,并求出当S最大时的值.
41. 根据素材回答问题:素材1
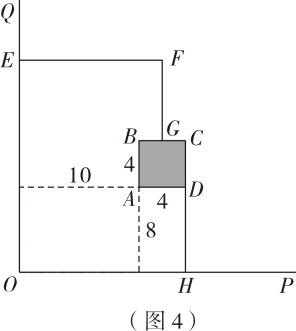
如图1,空地上有两条互相垂直的小路OP,OQ,中间有一正方形ABCD水池,已知水池的边长为4 米,AB//OQ,AD//OP,且AB与OQ的距离为10 米,AD与OP的距离为8 米.
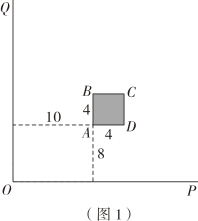
素材2
现利用两条小路,再购置30 米长的栅栏(图中的细实线)在空地上围出一个花圃,要求围起来的栅栏与小路相互平行(或垂直),靠小路和水池的都不需要栅栏,接口损耗忽略不计.
任务1
任务2
小明同学按如图2的设计,若EF=16米,求出花圃的面积(不包含水池的面积).
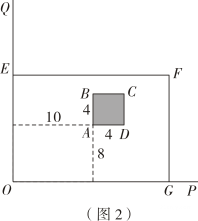
若按如图3、如图4设计方案,通过计算说明哪种方案的最大面积更大.
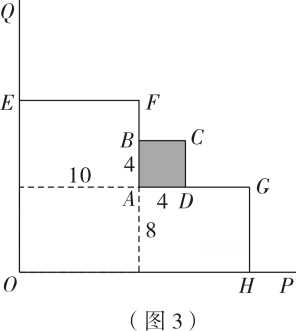
项目反 思
如果栅栏不一定与墙面垂直(或平行),你还能设计出比以上方案面积更大的花圃吗?某学习小组在探究的过程中,设计了方案如图5,你认为图5的最大面积与以上方案比较,哪个更大,请通过计算说明.