备考2024年中考数学探究性训练专题13 一次函数
试卷更新日期:2024-03-24 类型:二轮复习
一、选择题
-
1. 小星在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线 ,其中 ,则他探究这7条直线的交点个数最多是( )A、17个 B、18个 C、19个 D、21个
二、填空题
-
2. 如图,已知点 , , 直线经过点试探究:直线与线段有交点时的变化情况,猜想的取值范围是 .
 3. 在平面直角坐标系xOy中,已知直线l:y=x , 作A1(1,0)关于y=x的对称点B1 , 将点B1向右水平平移2个单位得到点A2;再作A2关于y=x的对称点B2 , 将点B2向右水平平移2个单位得到点A3;….请继续操作并探究:点A3的坐标是 , 点B2014的坐标是 .4. 已知合肥到芜湖的距离为千米,现有一辆邮政车往返两城市之间,该邮政车每次到达合肥或芜湖后,均需停留小时再重新出发.暑假期间,合肥某旅游公司计划在同线路上加开一辆旅游大巴车,在试运行期间,该邮政车与旅游大巴车同时从合肥出发,两辆车均保持匀速行驶,经过小时两车第一次相遇.两车之间的距离千米与行驶时间小时之间的部分函数关系如图所示.已知行驶过程时,邮政车的速度大于旅游大巴车的速度,请完成以下探究:
3. 在平面直角坐标系xOy中,已知直线l:y=x , 作A1(1,0)关于y=x的对称点B1 , 将点B1向右水平平移2个单位得到点A2;再作A2关于y=x的对称点B2 , 将点B2向右水平平移2个单位得到点A3;….请继续操作并探究:点A3的坐标是 , 点B2014的坐标是 .4. 已知合肥到芜湖的距离为千米,现有一辆邮政车往返两城市之间,该邮政车每次到达合肥或芜湖后,均需停留小时再重新出发.暑假期间,合肥某旅游公司计划在同线路上加开一辆旅游大巴车,在试运行期间,该邮政车与旅游大巴车同时从合肥出发,两辆车均保持匀速行驶,经过小时两车第一次相遇.两车之间的距离千米与行驶时间小时之间的部分函数关系如图所示.已知行驶过程时,邮政车的速度大于旅游大巴车的速度,请完成以下探究: (1)、邮政车的速度为千米小时;(2)、当两车第一次在行驶的路上相遇时,相遇点到合肥的距离为千米.5. 图象法是函数的表示方法之一,下面我们就一类特殊的函数图象展开探究.
(1)、邮政车的速度为千米小时;(2)、当两车第一次在行驶的路上相遇时,相遇点到合肥的距离为千米.5. 图象法是函数的表示方法之一,下面我们就一类特殊的函数图象展开探究.…
-3
-2
-1
0
1
2
3
…
…
6
4
2
0
2
4
6
…
画函数的图象,经历列表、描点、连线过程得到函数图象如图所示:
探究发现:函数的图象是由向右平移2个单位得到;
函数的图象是由向上平移3个单位得到.
 (1)、函数的最小值为;(2)、函数在中有最小值4,则的值是.
(1)、函数的最小值为;(2)、函数在中有最小值4,则的值是.三、理论探究题
-
6. 定义:我们把一次函数与正比例函数的交点称为一次函数的“不动点”.例如求的“不动点”;联立方程 , 解得 , 则的“不动点”为 .(1)、由定义可知,求一次函数的“不动点”.(2)、若一次函数的“不动点”为 , 求的值.(3)、若直线与x轴交于点 , 与轴交于点 , 且直线上没有“不动点”,若点为轴上一个动点,使得 , 求满足条件的点坐标.
四、数形结合探究题
-
7. 探究函数性质时,我们经历了列表、描点、连线画出函数的图象,观察分析图象特征,概括函数性质的过程.小腾根据学习函数的经验,对函数与进行了探究.下面是小腾的探究过程,请补充完整:(1)、绘制函数图象
①列表:下表是与 , 的几组对应值;
…
0
1
…
…
0
2
…
…
b
5
…
其中,b= ▲ ;
②描点、连线:在同一平面直角坐标系xOy中,描出上表中各组数值所对应的点 , 并画出函数 , 的图象.
 (2)、结合函数图象,探究函数性质
(2)、结合函数图象,探究函数性质①函数 , 的图象的交点坐标为 ▲ ,则关于x , y的二元一次方程组的解是 ▲ ;
②过点作垂直于x轴的直线与函数 , 的图象分别交于点P , Q , 当点P位于点Q下方时,的取值范围是 ▲ .
8. 小宇根据学习一次函数的经验,对函数的图象与性质进行了探究.下面是他的探究过程,请补充完整.(1)、如表列出了部分研究数据:x
…
0
1
2
3
4
…
y
…
2
1
0
a
0
1
…
上表的值为;
(2)、在如图所示的平面直角坐标系中,描出上表中各组对应值为坐标的点,并画出该函数图象; (3)、结合函数图象,写出该函数的两条性质.9. 数学小组在学习“一元一次不等式与一次函数”这一节课后,尝试解决“一元一次不等式与其它函数”的关系问题.他们确定以函数y=|x+1|为研究对象,通过作图,观察图象,归纳性质等探究过程,进一步理解一元一次不等式与函数的关系.
(3)、结合函数图象,写出该函数的两条性质.9. 数学小组在学习“一元一次不等式与一次函数”这一节课后,尝试解决“一元一次不等式与其它函数”的关系问题.他们确定以函数y=|x+1|为研究对象,通过作图,观察图象,归纳性质等探究过程,进一步理解一元一次不等式与函数的关系.请根据以下探究过程,回答问题.
 (1)、作出函数y=|x+1|的图象.
(1)、作出函数y=|x+1|的图象.①列表:
x
…
-4
-3
-2
-1
0
1
2
…
y
…
3
a
1
0
1
2
3
…
其中,表格中a的值为 ▲ ;
②描点,连线:
根据表格的数据,请在直角坐标系中描出对应值为坐标的点,并画出该函数的图象;
(2)、观察函数y=|x+1|的图象,回答下列问题:①当x=时,函数y=|x+1|有最小值,最小值为;
②当时(填自变量x的取值范围),y随x的增大而增大;
(3)、已知直线 , 请结合图象,直接写出不等式的解集是;(4)、若直线与y=|x+1|有2个交点,则k的取值范围是 .10. 探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程.结合已有的学习经验,请画出函数y=﹣ 的图象并探究该函数的性质.x
…
﹣4
﹣3
﹣2
﹣1
0
1
2
3
4
…
y
…
﹣
a
﹣2
﹣4
b
﹣4
﹣2
﹣
﹣
…
(1)、列表,写出表中a,b的值:a=_▲__,b=__▲_;描点、连线,在所给的平面直角坐标系中画出该函数的图象.
(2)、观察函数图象,判断下列关于函数性质的结论是否正确(在答题卡相应位置正确的用“√”作答,错误的用“×”作答):①函数y=﹣ 的图象关于y轴对称;
②当x=0时,函数y=﹣ 有最小值,最小值为﹣6;
③在自变量的取值范围内函数y的值随自变量x的增大而减小.
(3)、已知函数y=﹣ x﹣ 的图象如图所示,结合你所画的函数图象,直接写出不等式﹣ <﹣ x﹣ 的解集. 11. 探究函数性质时,我们经历了列表、描点、连线画出函数的图象,观察分析图象特征,概括函数性质的过程.结合已有的学习经验,请画出函数的图象并探究该函数的性质.
11. 探究函数性质时,我们经历了列表、描点、连线画出函数的图象,观察分析图象特征,概括函数性质的过程.结合已有的学习经验,请画出函数的图象并探究该函数的性质.x
…
0
1
2
3
…
y
…
a
0
2
b
…
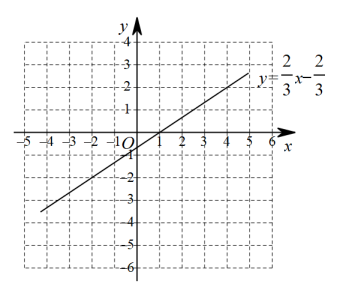 (1)、列表:写出表格中a,b的值: , ;(2)、通过描点、连线,在所给的平面直角坐标系中画出该函数的图象 , 并根据图象写出该函数的一条性质;(3)、已知函数的图象如图所示,请结合图象,直接写出不等式的解集 .12. 有这样一个问题:探究函数的图象与性质.小明根据学习函数的经验,对函数的图象与性质进行了探究.下面是小明的探究过程,请补充完整.
(1)、列表:写出表格中a,b的值: , ;(2)、通过描点、连线,在所给的平面直角坐标系中画出该函数的图象 , 并根据图象写出该函数的一条性质;(3)、已知函数的图象如图所示,请结合图象,直接写出不等式的解集 .12. 有这样一个问题:探究函数的图象与性质.小明根据学习函数的经验,对函数的图象与性质进行了探究.下面是小明的探究过程,请补充完整. (1)、化简函数表达式:当时,;当时,;(2)、如图,在平面直角坐标系中,通过列表描点画出了时的部分图象,请在同一平面直角坐标系中,补全当时的部分图象,并写出函数的两条性质;(3)、进一步研究:若点都在函数的图象上,且 , , 若存在满足 , 求的取值范围.13. 探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程.结合已有的学习经验,请画出函数的图象并探究该函数的性质.(1)、绘制函数图象
(1)、化简函数表达式:当时,;当时,;(2)、如图,在平面直角坐标系中,通过列表描点画出了时的部分图象,请在同一平面直角坐标系中,补全当时的部分图象,并写出函数的两条性质;(3)、进一步研究:若点都在函数的图象上,且 , , 若存在满足 , 求的取值范围.13. 探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程.结合已有的学习经验,请画出函数的图象并探究该函数的性质.(1)、绘制函数图象①列表:下表是x与y的几组对应值,其中m=;
x
…
0
1
2
3
…
y
…
1
2
3
4
3
m
1
…
②描点:根据表中的数值描点 , 补充描出点;
③连线:用平滑的曲线顺次连接各点,画出函数图象.
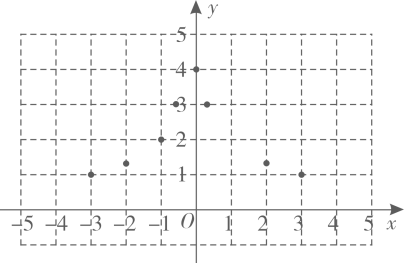 (2)、探究函数性质
(2)、探究函数性质写出函数的一条性质: .
(3)、运用函数图象及性质①观察你所画的函数图象,回答问题:若点 , 为该函数图象上不同的两点,则;
②根据函数图象,写出不等式的解集是 .
14. 探究函数性质时,我们经历了列表、描点、连线画函数图象,观察分析图象特征,概括函数性质的过程.以下是我们研究函数性质及其应用的部分过程,请按要求完成下列各小题.0
1
2
3
4
5
6
5
4
2
1
7
(1)、写出函数关系式中及表格中 , 的值:, , ;
(2)、根据表格中的数据在所给的平面直角坐标系中画出该函数的图象,并根据图象写出该函数的一条性质: ;(3)、已知函数的图象如图所示,结合你所画的函数图象,直接写出不等式的解集. 15. (数学问题)在同一直角坐标系内直线 与 ,当 满足什么条件时,这两条直线互相垂直?
15. (数学问题)在同一直角坐标系内直线 与 ,当 满足什么条件时,这两条直线互相垂直?探究问题:我们采取一般问题特殊化的策略来进行探究.
探究一:如图①,在同一直角坐标系内直线 与 有怎样的位置关系?
解:如图①,设点 在直线 上,则点 一定在直线 上.过点 分别作 的垂线,垂足分别为 .
则 ,
∴
∵
∴
所以,在同一直角坐标系内直线 与 互相垂直.

探究二:如图②,在同一直角坐标系内直线 上,则点 一定在直线 上.过点 分别作 轴的垂线,垂足分别为 .
∵ , , ,
∴ ,
又∵
∴
∴
又∵
∴
∵
∴
所以,在同一直角坐标系内直线 与 互相垂直.
探究三:如图③,在同一直角坐标系内直线 与 有怎样的位置关系?
(仿照上述方法解答,写出探究过程)
(1)、在同一直角坐标系内直线 与 ,当 满足数量关系为时,这两条直线互相垂直.(2)、在同一直角坐标系内已知直线 与直线 ,使它与直线 互相垂直, 的值为:;两直线垂足的坐标为: .16. 如图,在等腰中, , , 点为中点,点从点出发,沿方向以每秒的速度匀速运动到点设点的运动时间为秒,的面积为 .
根据学习函数的经验,对函数随自变量的变化规律进行探究. (1)、直接写出与的函数关系式,注明的取值范围,并画出的函数图象;(2)、观察的函数图象,写出一条该函数的性质;(3)、观察图象,直接写出当时,的值 ▲ 保留位小数,误差不超过17. 有这样一个问题:探究函数 的图象与性质.
(1)、直接写出与的函数关系式,注明的取值范围,并画出的函数图象;(2)、观察的函数图象,写出一条该函数的性质;(3)、观察图象,直接写出当时,的值 ▲ 保留位小数,误差不超过17. 有这样一个问题:探究函数 的图象与性质.小东根据学习函数的经验,对函数 的图象与性质进行了探究.
下面是小东的探究过程,请补充完成:
(1)、化简函数解析式,当 时, , 当 时 ;(2)、根据(1)中的结果,请在所给坐标系中画出函数 的图象;备用图 (3)、结合画出的函数图象,解决问题:若关于 的方程 只有一个实数根,直接写出实数a的取值范围: .18. 学习“一次函数”时,我们从“数”和“形”两方面研究一次函数的性质,并积累了一些经验和方法.小聪同学尝试运用积累的经验和方法对函数的图像与性质进行探究,下面是小聪同学的探究过程,请你补充完整.(1)、列表:
(3)、结合画出的函数图象,解决问题:若关于 的方程 只有一个实数根,直接写出实数a的取值范围: .18. 学习“一次函数”时,我们从“数”和“形”两方面研究一次函数的性质,并积累了一些经验和方法.小聪同学尝试运用积累的经验和方法对函数的图像与性质进行探究,下面是小聪同学的探究过程,请你补充完整.(1)、列表:x
…
0
1
2
3
4
…
y
…
1
0
a
b
1
…
则 , .
(2)、描点并画出该函数的图象;(3)、①请写出一条关于函数的性质:;②观察函数图象,当时,x的取值范围是;
③观察图像,直接写出函数的最小值 .
19. 如图
问题提出:
如图,等腰中, , , 直线经过点C,过点A作于点D,过点B作于点E,求证: ;
问题探究:
如图2,在平面直角坐标系中,一次函数与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角 , , 求点C的坐标;
问题解决:
古城西安已经全面迎来地铁时代!继西安地铁2号线于2011年9月16日通车试运行以来,共有八条线路开通运营,极大促进了西安市的交通运输,目前还有多条线路正在修建中.如图,地铁某线路原计划按OA-AB的方向施工,由于在AB方向发现一处地下古建筑,地铁修建须绕开此区域.经实地勘测,若将AB段绕点A顺时针或逆时针方向旋转45°至AC或AD方向,则可以绕开此区域.已知OA长为1千米,以点O为原点,OA所在直线为x轴,1千米为单位长度,建立平面直角坐标系,且射线AB与直线平行,请帮助施工队计算出AC和AD所在直线的解析式.
20. 数学小组在学习“一元一次不等式与一次函数”这一节课后,尝试解决“一元一次不等式与其它函数”的关系问题.他们确定以函数为研究对象,通过作图,观察图象,归纳性质等探究过程,进一步理解一元一次不等式与函数的关系.
请根据以下探究过程,回答问题.
(1)、作出函数的图象.①列表:
…
0
1
2
…
…
3
1
0
1
2
3
…
其中,表格中的值为 ▲ ;
②描点,连线:
根据表格的数据,请在直角坐标系中描出对应值为坐标的点,并画出该函数的图象;
(2)、观察函数的图象,回答下列问题:①当时,函数有最小值,最小值为;
②当时(填自变量的取值范围),随的增大而增大;
(3)、已知直线 , 请结合图象,直接写出不等式的解集是;(4)、若直线与有2个交点,则的取值范围是 .21. 【定义】如图1,在同一平面内,点在线段所在直线的两侧,若 , 且 , 则称点与是线段的等垂对称点。 (1)、【理解】如图2,在正方形网格中,点均在格点上,连接 , 则下列各组点是线段的等垂对称点的是;(填序号)
(1)、【理解】如图2,在正方形网格中,点均在格点上,连接 , 则下列各组点是线段的等垂对称点的是;(填序号)①点与点 ②点与点 ③点与点 ④点与点
(2)、如图3,在四边形中,是边上一点,点与是线段的等垂对称点,①求证:;
②若平分 , 试探究与之间的数量关系,并说明理由。
(3)、【拓展】如图4,已知直线与坐标轴交于点 , 直线与坐标轴交于点 , 当点中恰有两点是线段的等垂对称点,且时,请直接写出线段的长。22. 先阅读下列材料,然后解决问题:【阅读感悟】
在平面直角坐标系中,已知点 , 当t的值发生改变时,点Q的位置也会发生改变,为了求点Q运动所形成的图象的解析式,令点Q的横坐标x , 纵坐标y , 得到了方程组消去t , 得 , 即 , 可以发现,点随t的变化而运动所形成的图象的解析式是 .
(1)、【尝试应用】观察下列四个点的坐标,不在函数图象上的是____.
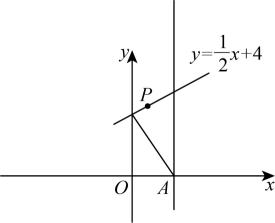
A、 B、 C、 D、(2)、求点随t的变化而运动所形成的图象的解析式;(3)、【综合运用】如图,在平面直角坐标系中,点P在一次函数的图象上运动.已知点为定点,连接 , 过点A作直线 , 且 , 求点B随点P的变化而运动所形成的图象的解析式.
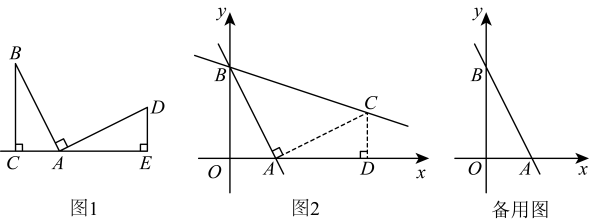
 23. 【探索发现】如图1,等腰直角三角形ABC中, , , 直线DE经过点 , 过作于点 . 过作于点 , 则 , 我们称这种全等模型为“型全等”.(不需要证明)
23. 【探索发现】如图1,等腰直角三角形ABC中, , , 直线DE经过点 , 过作于点 . 过作于点 , 则 , 我们称这种全等模型为“型全等”.(不需要证明)【迁移应用】已知:直线的图象与轴、轴分别交于A、B两点.
图1
 图2
图2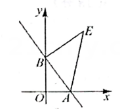 图3
图3 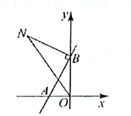 图4
图4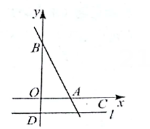 (1)、如图2,当时,在第一象限构造等腰直角 , ;直接写出 , ;(2)、如图3,当的取值变化,点随之在轴负半轴上运动时,在轴左侧过点B作 , 并且 , 连接ON,问的面积是否发生变化?若不变,求出其值;若变,请说明理由;(3)、【拓展应用】如图4,当时,直线与轴交于点 , 点、分别是直线和直线AB上的动点,点在轴上们坐标为 , 当是以CQ为斜边的等腰直角三角形时,点的坐标是 .24. 综合与探究:如图1,平面直角坐标系中,一次函数图象分别交轴、轴于点 , 一次函数的图象经过点 , 并与轴交于点 ,
(1)、如图2,当时,在第一象限构造等腰直角 , ;直接写出 , ;(2)、如图3,当的取值变化,点随之在轴负半轴上运动时,在轴左侧过点B作 , 并且 , 连接ON,问的面积是否发生变化?若不变,求出其值;若变,请说明理由;(3)、【拓展应用】如图4,当时,直线与轴交于点 , 点、分别是直线和直线AB上的动点,点在轴上们坐标为 , 当是以CQ为斜边的等腰直角三角形时,点的坐标是 .24. 综合与探究:如图1,平面直角坐标系中,一次函数图象分别交轴、轴于点 , 一次函数的图象经过点 , 并与轴交于点 , (1)、 , 点的坐标为;(2)、小朱发现 , 请说明你的理由;(3)、如图2,点在直线上,过点作轴的平行线交直线与点 , 若点的横坐标为 , 则是的一半,请通过计算说明原因;(4)、若点关于轴的对称点为 , 点是直线上的一个动点,是否存在点 , 使?若存在,请直接写出点的坐标;若不存在,说明理由.25. 【模型介绍】
(1)、 , 点的坐标为;(2)、小朱发现 , 请说明你的理由;(3)、如图2,点在直线上,过点作轴的平行线交直线与点 , 若点的横坐标为 , 则是的一半,请通过计算说明原因;(4)、若点关于轴的对称点为 , 点是直线上的一个动点,是否存在点 , 使?若存在,请直接写出点的坐标;若不存在,说明理由.25. 【模型介绍】如图 , , , 过点作于点 , 过点作于点 . 则 . 我们把这个数学模型称为“字”模型或“一线三等角”模型.
【模型应用】
在平面直角坐标系中,直线与轴交于点 , 与轴交于点 .
(1)、如图 , 将直线绕点逆时针旋转 , 得到直线 , 求直线的表达式.下面是小明的想法,请你帮助完成.小明想利用“一线三等角”模型解决这个问题.如图,过点作的垂线交于点 , 再过点作轴的垂线,垂足为 , 可求出点的坐标为 , 从而求得直线的表达式为 .
(2)、若将直线绕点顺时针旋转 , 所得直线的表达式为 .(3)、点是线段上的一个动点,点是线段上一动点,若是等腰直角三角形,且 , 则点的坐标是 .五、实践探究题
-
26. 根据表中素材,探索完成以下任务:
建设“美丽乡村”,落实“乡村振兴”
问题情境
素材1
已知甲、乙两仓库分别有水泥40吨和60吨.
素材2
现在A村需要水泥48吨,B村需要水泥52吨.
素材3
从甲仓库往A,B两村运送水泥的费用分别为20元/吨和25元/吨;
从乙仓库往A,B两村运送水泥的费用分别为15元/吨和24元/吨.
问题解决
分析
设从甲仓库运往A村水泥x吨,补全以下表格.
运量(吨)
运费(元)
甲仓库
乙仓库
甲仓库
乙仓库
A村
x
B村
① ▲
② ▲
问题1
设总运费为y元,请写出y与x的函数关系式并求出最少总运费.
问题2
为了更好地支援乡村建设,甲仓库运往A村的运费每吨减少元,这时甲仓库运往A村的水泥多少吨时总运费最少?最少费用为多少元?(用含a的代数式表示)
27. 缂丝,是中国传统丝绸艺术品中的精华.缂丝织造技艺主要是使用古老的木机(如图①)及若干竹制的梭子和拨子,经过“通经断纬”的织造方法,将五彩的蚕丝线缂织成一幅色彩丰富的织物.缂丝工匠现要完成一件织品,工作一段时间后,记录了工作时间和织品长度的数据变化,并从函数角度进行了如下实验探究.
图①
【数据观察】记录的工作时间x(时)和织品长度y(厘米)的数据变化,如下表:
工作时间x(时)
0
2
4
6
8
织品长度y(厘米)
3
3.6
4.2
4.8
5.4
【探索发现】
(1)、建立平面直角坐标系,如图②,横轴表示记录的工作时间x , 纵轴表示织品长度y , 描出以表格中数据为坐标的各点.
图②
(2)、观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式,如果不在同一条直线上,说明理由.(3)、如果每天工作10小时,要完成长为240厘米的织品,共需要多少天?28. 小明观察到一个水龙头因损坏而不断地向外滴水,为探究其漏水造成的浪费情况,小明用一个带有刻度的量筒放在水龙头下面装水,每隔一分钟记录量筒中的总水量,但由于操作延误,开始计时的时候量筒中已经有少量水,因而得到如表的一组数据:时间t(分钟)
1
2
3
4
5
***
总水量y(毫升)
7
12
17
22
27
…
(1)、探究:根据上表中的数据,请判断和y=kt+b(k,b为常数,k≠0)哪一个能正确反映总水量y与时间t的函数关系,并求出y关于t的函数表达式.(2)、应用:①请你估算小明在第20分钟测量时量筒的总水量是多少毫升.
②一个人一天大约饮用1500毫升水,请你估算这个水龙头一个月(按30天计)的漏水量可供一人饮用多少天.
29. 综合与实践:.【问题情境】
小莹妈妈的花卉超市以15元/盆的价格新购进了某种盆栽花卉,为了确定售价,小莹帮妈妈调查了附近A,B,C,D,E五家花卉店近期该种盆栽花卉的售价与日销售量情况,记录如下:
售价(元/盆) 日销售量(盆) A 20 50 B 30 30 C 18 54 D 22 46 E 26 38 【数据整理】
(1)、请将以上调查数据按照一定顺序重新整理,填写在下表中:售价(元/盆)
日销售量(盆)
(2)、分析数据的变化规律,找出日销售量与售价间的关系.(3)、根据以上信息,小莹妈妈在销售该种花卉中,①要想每天获得400元的利润,应如何定价?
②售价定为多少时,每天能够获得最大利润?
冲剌高分练
30. 某课外科技活动小组研制了一种航模飞机.通过实验,收集了飞机相对于出发点的飞行水平距离(单位:)以、飞行高度(单位:)随飞行时间(单位:)变化的数据如下表.飞行时间
0
2
4
6
8
…
飞行水平距离
0
10
20
30
40
…
飞行高度
0
22
40
54
64
…
(1)、探究发现:与 , 与之间的数量关系可以用我们已学过的函数来描述.直接写出关于的函数解析式和关于的函数解析式(不要求写出自变量的取值范围).(2)、问题解决:如图,活动小组在水平安全线上处设置一个高度可以变化的发射平台试飞该航模飞机.根据上面的探究发现解决下列问题.
①若发射平台相对于安全线的高度为0m,求飞机落到安全线时飞行的水平距离;
②在安全线上设置回收区域 . 若飞机落到内(不包括端点),求发射平台相对于安全线的高度的变化范围.
31. 五子棋的比赛规则是:只要同色5子连成一条直线为胜利.如图是两人玩的一盘棋,若白棋①的位置是(1,﹣5),黑棋②的位置是(2,﹣4).解答下列问题: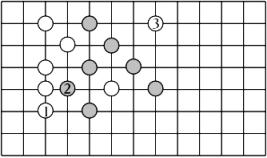 (1)、白棋③的位置是 ;(2)、如果现在轮到黑棋走,黑棋放在 位置就获得胜利了;(3)、如果现在轮到白棋走,白棋放在 位置就获得胜利了.(4)、在(2)的条件下,黑棋获胜了.
(1)、白棋③的位置是 ;(2)、如果现在轮到黑棋走,黑棋放在 位置就获得胜利了;(3)、如果现在轮到白棋走,白棋放在 位置就获得胜利了.(4)、在(2)的条件下,黑棋获胜了.①设此时黑色5子连成直线的表达式是y=ax+b,则方程ax+b=0的解是 .
②若黑色5子连成直线的表达式中y<0,则x的取值范围是 .
32. 综合与实践.【问题情境】“漏壶”是一种古代计时器,在社会实践活动中,某小组同学根据“漏壶”的原理制作了如图(a)所示的液体漏壶,该漏壶是由一个圆锥和一个圆柱组成的,中间连通,液体可以从圆锥容器中匀速漏到圆柱容器中,实验开始时圆柱容器中已有一部分液体.

【实验观察】下表是实验记录的圆柱容器液面高度与时间的数据:
时间 1 2 3 4 5 6圆柱容器液面高度 6 10 14 18 22 (1)、【探索发现】请你根据表中的数据在图(b)中描点、连线,用所学过的一次函数的知识确定与之间的函数表达式;
(2)、【结论应用】如果本次实验记录的开始时间是上午 , 那么当圆柱容器液面高度达到时是几点?
33.

 (1)、问题发现:
(1)、问题发现:如图1,等腰直角置于平面直角坐标系中,点 , 的坐标分别为 , , 是上一点, , 则点的坐标为
(2)、问题探究:如图2,若点 , 的坐标分别为 , , 其余条件与(1)相同,求经过 , 两点的直线表达式。(3)、问题解决:国庆前夕,大唐芙蓉园景区为了提高服务质量,想尽可能美化每一个角落,给游客美的享受.如图3,是景区东门的广场一角,两面墙互相垂直,景区管理部门设计将 , 墙面布置成历史人文宣传墙,边上用建筑隔板搭出段将该角落与广场其他区域隔开,段布置成长安八景图,剩余部分为广场角出入口,内部空间放置一些绿植和供游人休息的桌椅,考虑到出入安全,还需在靠近出入口的处建一个安检点.已知 , , 平分 , 安检点在与的交点处.求点分别到 , 墙面的距离。34. 综合与实践如图1,某兴趣小组计划开垦一个面积为的矩形地块种植农作物,地块一边靠墙,另外三边用木栏围住,木栏总长为 .

【问题提出】
小组同学提出这样一个问题:若 , 能否围出矩形地块?
【问题探究】
小颖尝试从“函数图象”的角度解决这个问题:
设为 , 为 . 由矩形地块面积为 , 得到 , 满足条件的可看成是反比例函数的图象在第一象限内点的坐标;木栏总长为 , 得到 , 满足条件的可看成一次函数的图象在第一象限内点的坐标,同时满足这两个条件的就可以看成两个函数图象交点的坐标.
如图2,反比例函数的图象与直线:的交点坐标为和 ▲ , 因此,木栏总长为时,能围出矩形地块,分别为: , ;或 ▲ m , ▲ m .
 (1)、根据小颖的分析思路,完成上面的填空.(2)、【类比探究】
(1)、根据小颖的分析思路,完成上面的填空.(2)、【类比探究】若 , 能否围出矩形地块?请仿照小颖的方法,在图2中画出一次函数图象并说明理由.
(3)、【问题延伸】当木栏总长为时,小颖建立了一次函数 . 发现直线可以看成是直线通过平移得到的,在平移过程中,当过点时,直线与反比例函数的图象有唯一交点.
请在图2中画出直线过点时的图象,并求出的值.
(4)、【拓展应用】小颖从以上探究中发现“能否围成矩形地块问题”可以转化为“与图象在第一象限内交点的存在问题”.
若要围出满足条件的矩形地块,且和的长均不小于 , 请直接写出的取值范围.
-
-