备考2024年中考数学探究性训练专题12 分式方程

试卷更新日期：2024-03-24 类型：二轮复习

进入出卷网下载

一、选择题

1. 数学家们在研究15、12、10这三个数的倒数时发现： $\frac{1}{12} - \frac{1}{15} = \frac{1}{10} - \frac{1}{12}$ ．因此就将具有这样性质的三个数称之为调和数，如6、3、2也是一组调和数．现有一组调和数：x、5、3（x>5），则x的值是（）

A、6 B、7.5 C、12 D、15

查看试题解析

二、填空题

2. 数学的美学无处不在，数学家们研究发现，弹拨琴弦发出声音的音调高低取决于弦的长度，绷得一样紧的几根弦，如果长度的比能够表示成整数的比，发出的声音就比较和谐.例如，三根弦长度之比是15：12：10，把它们绷得一样紧，用同样的力弹拨，它们将分别发出调和的乐声do、mi、so.研究15、12、10这三个数的倒数发现： $\frac{1}{12} - \frac{1}{15} = \frac{1}{10} - \frac{1}{12}$ .我们称15、12、10这三个数为一组调和数.现有一组调和数：x、6、4（x＞6），则x的值是.

查看试题解析
3. 整体思想就是通过研究问题的整体形式从面对问题进行整体处理的解题方法．如 ${\begin{array}{l} \frac{1}{x} + \frac{1}{y} = 3 \\ \frac{2}{x} + \frac{3}{y} = 7 \end{array}$ ，此题设“ $\frac{1}{x} = a$ ， $\frac{1}{y} = b$ ”，得方程 ${\begin{array}{l} a + b = 3 \\ 2 a + 3 b = 7 \end{array}$ ，解得 ${\begin{array}{l} a = 2 \\ b = 1 \end{array}$ ， $∴ {\begin{array}{l} x = 0.5 \\ y = 1 \end{array}$ ．利用整体思想解决问题：采采家准备装修-厨房，若甲，乙两个装修公司，合做 $6$ 需周完成，甲公司单独做4周后，剩下的由乙公司来做，还需 $9$ 周才能完成，设甲公司单独完成需 $x$ 周，乙公司单独完成需 $y$ 周，则得到方程．利用整体思想，解得．

查看试题解析

三、理论探究题

4. （探索发现）
先观察下面给出的等式，探究其隐含的规律，然后回答问题： $\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ； $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ； $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ； $\dots$

(1)、若 $n$ 为正整数，直接写出结果： $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{n (n + 1)} =$ ．

(2)、（拓展延伸）
根据上面探索的规律，解决下面的问题：

解关于 $x$ 的分式方程： $\frac{1}{(x - 1) (x - 2)} - \frac{1}{(x - 2) (x - 3)} - \frac{2}{(x - 1) (x - 3)} = \frac{x - 5}{x - 3}$ ．

查看试题解析
5. 探索发现： $\frac{1}{1 \times 2}$ ＝1﹣ $\frac{1}{2}$ ， $\frac{1}{2 \times 3}$ ＝ $\frac{1}{2}$ ﹣ $\frac{1}{3}$ ， $\frac{1}{3 \times 4}$ ＝ $\frac{1}{3}$ ﹣ $\frac{1}{4}$ …，根据你发现的规律，回答下列问题：

(1)、 $\frac{1}{5 \times 6}$ ＝， $\frac{1}{n \times (n + 1)}$ ＝；

(2)、利用你发现的规律计算： $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ +…+ $\frac{1}{2018 \times 2019}$ ；

(3)、灵活利用规律解方程： $\frac{1}{x (x + 3)}$ + $\frac{1}{(x + 3) (x + 6)}$ +…+ $\frac{1}{(x + 96) (x + 99)}$ ＝ $\frac{1}{x + 99}$ ．

查看试题解析
6. 阅读下列材料：
在学习“分式方程及其解法”过程中，老师提出一个问题：若关于x的分式方程 $\frac{a}{x - 1} + \frac{3}{1 - x} = 1$ 的解为正数，求a的取值范围？

经过小组交流讨论后，同学们逐渐形成了两种意见：

小明说：解这个关于x的分式方程，得到方程的解为x=a﹣2．由题意可得a﹣2＞0，所以a＞2，问题解决．

小强说：你考虑的不全面．还必须保证a≠3才行．

老师说：小强所说完全正确．

请回答：小明考虑问题不全面，主要体现在哪里？请你简要说明：．

完成下列问题：

(1)、已知关于x的方程 $\frac{2 m x - 1}{x + 2}$ =1的解为负数，求m的取值范围；

(2)、若关于x的分式方程 $\frac{3 - 2 x}{x - 3} + \frac{2 - n x}{3 - x}$ =﹣1无解．直接写出n的取值范围．

查看试题解析
7. 阅读：分式 $\frac{3 x - 2}{x + 1}$ 可进行如下变形： $\frac{3 x - 2}{x + 1} = \frac{3 (x + 1) - 5}{x + 1} = 3 - \frac{5}{x + 1}$ ．

(1)、探索：如果 $\frac{5 x - 3}{x + 2} = 5 + \frac{m}{x + 2}$ ，则m＝；

(2)、总结：如果 $\frac{a x + b}{x + c} = a + \frac{m}{x + c}$ （其中a ， b ， c为常数），则m＝；

(3)、应用：利用上述结论解决：若代数式 $\frac{4 x - 3}{x - 1}$ 的值为整数，求满足条件的整数x的值．

查看试题解析
8.

(1)、探究1：m为何值时，关于x方程 $\frac{3 x}{x - 3} + 5 = \frac{m}{3 - x}$ 有增根？

(2)、探究2：m为何值时，关于x方程 $\frac{3 x}{x - 3} + 5 = \frac{m}{3 - x}$ 的根是x=-1？

(3)、探究3：任意写出三个m的值，使对应的关于x方程 $\frac{3 x}{x - 3} + 5 = \frac{m}{3 - x}$ 的三个根中两个根之和等于第三个根？

(4)、探究4：你发现满足“探究3"条件的m₁ ， m₂ ， m₃的关系是.

查看试题解析
9. 小明邀请你参与数学接龙游戏：
【问题】解分式方程： $\frac{3 x}{x - 1} + \frac{x - 1}{3 x} = 2$
【小明解答的部分】解：设 $\frac{3 x}{x - 1} = t$ ，则 $\frac{x - 1}{3 x} = \frac{1}{t}$ 故原方程可化为 $t + \frac{1}{t} = 2$ ，去分母并移项，得 $t^{2} - 2 t + 1 = 0$
【接龙】

查看试题解析
10. 阅读材料，并完成下列问题：
不难求得方程x+ $\frac{1}{x}$ ＝2+ $\frac{1}{2}$ 的解是x₁＝2， $x_{2} = \frac{1}{2}$ ；

x- $\frac{1}{x}$ ＝3+ $\frac{1}{3}$ 的解是x₁＝3，x₂＝ $\frac{1}{3}$ ；

x $+ \frac{1}{x} = 4 + \frac{1}{4}$ 的解是x₁＝4，x₂＝ $\frac{1}{4}$ ；

(1)、观察上述方程及其解，可猜想关于x的方程x $+ \frac{1}{x} = a + \frac{1}{a} (a \neq 0)$ 的解是 .

(2)、试用“求出关于x的方程x $+ \frac{1}{x} = a + \frac{1}{a} (a \neq 0)$ 的解”的方法证明你的猜想；

(3)、利用你猜想的结论，解关于x的方程 $\frac{x^{2} - x + 1}{x - 1} = a + \frac{1}{a - 1}$ .

查看试题解析
11. 阅读材料：对于非零实数a，b，若关于x的分式 $\frac{(x - a) (x - b)}{x}$ 的值为零，则解得 $x_{1} = a ， x_{2} = b$ ．又因为 $\frac{(x - a) (x - b)}{x} = \frac{x^{2} - (a + b) x + a b}{x} = x + \frac{a b}{x} - (a + b)$ ，所以关于x的方程x+ $\frac{a b}{x} = a + b$ 的解为 $x_{1} = a ， x_{2} = b$ ．

(1)、【理解应用】解方程 $\frac{x^{2} + 2}{x} = 5 + \frac{2}{5}$ ；

(2)、【知识迁移】若关于x的方程 $x + \frac{3}{x} = 7$ 的解为 $x_{1} = a ， x_{2} = b$ ，求 $a^{2} + b^{2}$ 的值．

查看试题解析
12. 阅读下列材料，解决后面问题：① $x + \frac{1}{x} = c + \frac{1}{c}$ 的解为： $x_{1} = c$ ， $x_{2} = \frac{1}{c}$ ；② $x - \frac{1}{x} = c - \frac{1}{c}$ ，即 $x + \frac{- 1}{x} = c + \frac{- 1}{c}$ 的解为： $x_{1} = - c$ ， $x_{2} = - \frac{1}{c}$ ；③ $x + \frac{2}{x} = c + \frac{2}{c}$ 的解为： $x_{1} = c$ ， $x_{2} = \frac{2}{c}$ ；④ $x + \frac{3}{x} = c + \frac{3}{c}$ 的解为： $x_{1} = c$ ， $x_{2} = \frac{3}{c}$ ；…

(1)、请观察上述方程与解的特征，猜想方程 $x + \frac{π}{x} = c + \frac{π}{c}$ 的解，并验证你的结论；

(2)、利用你验证的结论解关于x的方程： $x + \frac{2}{x - 1} = a + \frac{2}{a - 1}$ ．

查看试题解析
13. 阅读材料：对于非零实数a，b，若关于x的分式 $\frac{(x - a) (x - b)}{x}$ 的值为零，则解得x₁＝a，x₂＝b．又因为 $\frac{(x - a) (x - b)}{x} = \frac{x^{2} - (a + b) x + a b}{x} = x + \frac{a b}{x}$ ﹣（a+b），所以关于x的方程x+ $\frac{a b}{x}$ ＝a+b的解为x₁＝a，x₂＝b．

(1)、理解应用：方程 $\frac{x^{2} + 2}{x} = 3 + \frac{2}{3}$ 的解为：x₁＝， x₂＝；

(2)、知识迁移：若关于x的方程x+ $\frac{3}{x}$ ＝5的解为x₁＝a，x₂＝b，求a²+b²的值；

(3)、拓展提升：若关于x的方程 $\frac{4}{x - 1}$ ＝k﹣x的解为x₁＝t+1，x₂＝t²+2，求k²﹣4k+2t³的值．

查看试题解析
14. 阅读材料：对于非零实数m，n，若关于x的分式 $\frac{(x - m) (x - n)}{x}$ 的值为零，则x＝m或x＝n.又因为 $\frac{(x - m) (x - n)}{x}$ ＝ $\frac{x^{2} - (m + n) x + m n}{x}$ ＝x+ $\frac{m m}{x}$ ﹣（m+n），所以关于x的方程x+ $\frac{m n}{x}$ ＝m+n的解为x₁＝m，x₂＝n.

(1)、理解应用：方程x+ $\frac{1}{x}$ ＝2+ $\frac{1}{2}$ 的解为：x₁＝， x₂＝；

(2)、拓展提升：若关于x的方程x+ $\frac{4}{x}$ ＝k﹣1的解满足x₁＝x₂ ，求k的值.

查看试题解析
15. 阅读理解，并解决问题.
分式方程的增根：解分式方程时可能会产生增根，原因是什么呢？事实上，解分式方程时产生增根，主要是在去分母这一步造成的.根据等式的基本性质2：等式两边乘同一个数，或除以同一个不为0的数，结果仍相等.但是，当等式两边同乘0时，就会出现 $0 = 0$ 的特殊情况.因此，解方程时，方程左右两边不能同乘0.而去分母时会在方程左右两边同乘公分母，此时无法知道所乘的公分母的值是否为0，于是，未知数的取值范围可能就扩大了.如果去分母后得到的整式方程的根使所乘的公分母值为0，此根即为增根，增根是整式方程的根，但不是原分式方程的根.所以解分式方程必须验根.请根据阅读材料解决问题：

(1)、若解分式方程 $\frac{1 - x}{x - 2} + 2 = \frac{1}{2 - x}$ 时产生了增根，这个增根是；

(2)、小明认为解分式方程 $\frac{2 x}{x^{2} + 1} - \frac{3}{2 x^{2} + 2} = 0$ 时，不会产生增根，请你直接写出原因；

(3)、解方程 $\frac{2}{x - 1} + \frac{1}{x + 1} = \frac{4}{x^{2} - 1}$

查看试题解析
16. 阅读材料：对于任何实数，我们规定符号“ $| \begin{array}{l} a & b \\ c & d \end{array} |$ ”称为二阶行列式，规定它的运算法则为： $| \begin{array}{l} a & b \\ c & d \end{array} |$ ＝ad－bc ．

(1)、按照这个规定请你计算 $| \begin{array}{l} 5 & 6 \\ 7 & - 8 \end{array} |$ 的值；

(2)、请你根据上述规定求出等式 $| \begin{matrix} 2 & 1 \\ \frac{1}{1 - x} & \frac{1}{x - 1} \end{matrix} |$ ＝1中 $x$ 的值．

查看试题解析
17. 我们把形如 $x + \frac{a b}{x} = a + b (a b \neq 0) ，$ 且两个解分别为：x₁=a，x₂=b的方程称为十字分式方程.
例如：若 $x + \frac{3}{x} = 4$ 为十字分式方程，则可将它化为 $x + \frac{1 \times 3}{x} = 1 + 3 ，$ 得 x₁ =1，x₂ =3.
再如：若 $x + \frac{8}{x} = - 6$ 为十字分式方程，则可将它化为 $x + \frac{(- 2) \times (- 4)}{x} = (- 2) + (- 4) ，$ 得 $x_{1} = - 2 ， x_{2} = -$ 4.
应用上面的结论解答下列问题：

(1)、若 $x + \frac{6}{x} = - 5$ 为十字分式方程，则x₁= ， x₂=.

(2)、若十字分式方程 $x - \frac{5}{x} = - 2$ 的两个解分别为 $x_{1} = m ， x_{2} = n ，$ 求 $\frac{n}{m} + \frac{m}{n}$ 的值.

(3)、若关于x的十字分式方程 $x - \frac{2 k^{2} + 3 k}{x - 2} = - k - 1$ 的两个解分别为 $x_{1} ， x_{2} （ k > 0 ， x_{1} > x_{2}) ，$ 求 $\frac{x_{1} - 2}{x_{2} + 1}$ 的值.

查看试题解析
18. 观察下列方程的特征及其解的特点；
①x+ $\frac{2}{x}$ ＝﹣3的解为x₁＝﹣1，x₂＝﹣2．
②x+ $\frac{6}{x}$ ＝﹣5的解为x₁＝﹣2，x₂＝﹣3．
③x+ $\frac{12}{x}$ ＝﹣7的解为x₁＝﹣3，x₂＝﹣4；
解答下列问题；

(1)、请你写出一个符合上述特征的方程为，其解为．

(2)、根据这类方程特征，写出第n个方程为，其解为．

(3)、请利用（2）的结论，求关于x的方程x+ $\frac{n^{2} + n}{x + 3}$ ＝﹣2（n+2）（其中n为正整数）的解．

查看试题解析
19. 先阅读下面的材料，然后回答问题：
方程x+ $\frac{1}{x}$ =2+ $\frac{1}{2}$ 的解为x₁=2，x₂= $\frac{1}{2}$ ；
方程x+ $\frac{1}{x}$ =3+ $\frac{1}{3}$ 的解为x₁=3，x₂= $\frac{1}{3}$ ；
方程x+ $\frac{1}{x}$ =4+ $\frac{1}{4}$ 的解为x₁=4，x₂= $\frac{1}{4}$
……

(1)、观察上述方程的解，猜想关于x的方程x+ $\frac{1}{x}$ =5+ $\frac{1}{5}$ 的解是.

(2)、根据上面的规律，猜想关于x的方程x+ $\frac{1}{x}$ =a+ $\frac{1}{a}$ 的解是.

(3)、猜想关于x的方程x- $\frac{1}{x}$ = $1 \frac{1}{2}$ 的解并验证你的结论

(4)、在解方程y+ $\frac{y + 2}{y + 1}$ = $\frac{10}{3}$ 时，可将方程变形转化为(2)的形式求解，按要求写出你的变形求解过程．

查看试题解析
20. 如果两个分式M与N的和为常数k ，且k为正整数，则称M与N互为“和整分式常数k称为“和整值”如分式 $M = \frac{x}{x + 1} ， N = \frac{1}{x + 1} ， M + N = \frac{x + 1}{x + 1} = 1$ ，则M与N互为“和整分式”，“和整值” $k = 1$ ．

(1)、已知分式 $A = \frac{x - 7}{x - 2} ， B = \frac{x^{2} + 3 x}{x^{2} - 2 x}$ ，判断A与B是否互为“和整分式”，若不是，请说明理由；若是，请求出“和整值”k；

(2)、已知分式 $C = \frac{3 x - 4}{x - 2} ， D = \frac{G}{x^{2} - 4}$ ， C与D互为“和整分式”，且“和整值” $k = 3$ ，若x为正整数，分式D的值为正整数t ．
①求G所代表的代数式：
②求x的值：

(3)、在（2）的条件下，已知分式 $P = \frac{3 x - 5}{x - 3} ， Q = \frac{m x - 3}{3 - x}$ ，且 $P + Q = t$ ，若该关于x的方程无解，求实数m的值．

查看试题解析
21. 苏科版九上数学 $p 31$ 阅读 $《$ 各类方程的解法 $》$ 中提到：各类方程的解法不尽相同，但是它们有一个共同的基本数学思想--转化，把未知转化为已知．
用“转化”的数学思想，我们还可以解一些新的方程．例如，一元三次方程 $x^{3} + x^{2} - 2 x = 0$ ，可以通过因式分解把它转化为 $x (x^{2} + x - 2) = 0$ ，解方程 $x = 0$ 和 $x^{2} + x - 2 = 0$ ，可得方程 $x^{3} + x^{2} - 2 x = 0$ 的解．

(1)、问题：方程 $x^{3} + x^{2} - 2 x = 0$ 的解是 $x_{1} = 0$ ， $x_{2} =$ ， $x_{3} =$ ；

(2)、用“转化”思想求方程 $\sqrt{2 x + 3} = x$ 的解；

(3)、拓展：若实数 $x$ 满足 $x^{2} + \frac{1}{x^{2}} - 3 x - \frac{3}{x} = 2$ ，求 $x + \frac{1}{x}$ 的值.

查看试题解析
22. 阅读材料，并完成下列问题：
已知分式方程：① $x + \frac{2}{x}$ ＝3，②x+ $\frac{6}{x}$ ＝5，③x+ $\frac{12}{x}$ ＝7．

其中，方程①的解有2个：x＝1或x＝2；方程②的解有2个：x＝2或x＝3；方程③的解有2个：x＝3或x＝4．

(1)、观察上述方程的特点，再观察方程的2个解与方程左边分式的分子、右边常数的关系，猜想方程x+ $\frac{30}{x}$ ＝11的解是．

(2)、关于x的方程x+ $\frac{2020}{x}$ ＝101+ $\frac{100}{m}$ 有2个解，它们是x＝101或x＝ $\frac{100}{m}$ ，根据所猜想的规律，求m的值．

查看试题解析
23. 阅读材料：
关于x的方程： $x + \frac{1}{x} = c + \frac{1}{c}$ 的解是 $x_{1} = c$ ， $x_{2} = \frac{1}{c}$ ；

$x - \frac{1}{x} = c - \frac{1}{c}$ （即 $x + \frac{- 1}{x} = c + \frac{- 1}{c}$ ）的解是 $x_{1} = c$ $x_{2} = - \frac{1}{c}$ ；

$x + \frac{2}{x} = c + \frac{2}{c}$ 的解是 $x_{1} = c$ ， $x_{2} = \frac{2}{c}$ ；

$x + \frac{3}{x} = c + \frac{3}{c}$ 的解是 $x_{1} = c$ ， $x_{2} = \frac{3}{c}$ ；……

(1)、请观察上述方程与解的特征，比较关于x的方程 $x + \frac{m}{x} = c + \frac{m}{c} (m \neq 0)$ 与它们的关系，猜想它的解是什么？并利用“方程的解”的概念进行验证。

(2)、由上述的观察、比较、猜想、验证，可以得出结论：
如果方程的左边是未知数与其倒数的倍数的和，方程的右边的形式与左边完全相同，只是把其中的未知数换成了某个常数，那么这样的方程可以直接得解，请用这个结论解关于x的方程： $x + \frac{2}{x - 1} = a + \frac{2}{a - 1}$ 。

查看试题解析

四、数形结合探究题

24. 综合与探究
如图，点A、点B分别在y轴、轴的正半轴上， OA：OB=3：4 ，且OA是方程 $\frac{4}{x^{2} - 4} = \frac{1}{x + 2}$ 的根．将△OAB 沿直线AC折叠，使点O落在线段 AB 上的点D处．

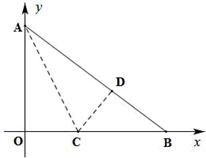(1)、求 OA、OB 的长；

(2)、求点C的坐标；

(3)、①若直线l经过点 E（0，-2）且平行于x轴，在直线 l 上找一点G ，使 AG+CG 最短，请你直接写出点 G 的坐标；
②在 x 轴上是否存在这样的点 M ，使得以点 A、C、M 为顶点的三角形为等腰三角形？若存在，请直接写出点 M 的坐标；若不存在，请说明理由．

查看试题解析

五、实践探究题

25.

(1)、问题背景：两个小组同时开始攀登一座450m高的山，第一组的攀登速度是第二组的1.2倍，他们比第二组早15min到达顶峰，求这两个小组的攀登速度各是多少？

(2)、尝试应用：如果山高为hm，第一组的攀登速度是第二组的a倍（其中a＞1），并且比第二组早tmin到达顶峰，设第一组的速度为 $V_{1}$ ，第二组的速度为 $V_{2}$ ．
①请直接写出 $V_{1} =$ ▲ ， $V_{2} =$ ▲ ．（结果用含h、a、t的式子表示）
②化简： $\frac{1}{V_{1} - V_{2}} - \frac{t}{h a - h}$ ．（结果用含h、a、t的式子表示）

(3)、拓展应用：在（2）的条件下，设 $V = V_{1} + V_{2}$ ， $a h = 1$ ，分解因式： $x^{2} - \frac{5 (a t V + h) x}{a} + \frac{6 (a t V + h)^{2}}{a^{2}} =$ （直接写出结果）

查看试题解析

26. 根据以下素材，探索完成任务．

如何设计奖品购买及兑换方案？
素材1	某文具店销售某种钢笔与笔记本，已知钢笔的单价是笔记本的2倍，用120元购买笔记本的数量比用160元购买钢笔的数量多8件．
素材2	某学校花费400元购买该文具店的钢笔和笔记本作为奖品颁发给“优秀学生”，购买钢笔和笔记本的数量之比为 $3 ： 2$ ．
素材3	学校花费400元后，文具店赠送 $m$ 张 $(1 < m < 10)$ 兑换券（如右）用于商品兑换．兑换后，笔记本与钢笔数量相同．
问题解决
任务1	探求商品单价	请运用适当方法，求出钢笔与笔记本的单价．
任务2	探究购买方案	探究购买钢笔和笔记本的数量．
任务3	确定兑换方式	运用数学知识，确定兑换方式．

查看试题解析

27. 【综合与实践】
学校在某商场购买甲、乙两种不同类型的足球，相关信息如下：购买甲种足球共用2000元，购买乙种足球共花费1400元.已知购买一个乙种足球比购买一个甲种足球多花20元.设购买一个甲种足球的单价是 $x$ 元。

(1)、请用含 $x$ 的代数式分别表示购买甲、乙两种足球的数量；

(2)、若本次购买甲种足球的数量是购买乙种足球数量的2倍，求甲、乙两种足球在此商场的销售单价；

(3)、为满足学生需求，这所学校决定再次购买甲、乙两种足球共50个.恰逢该商场对两种足球的销售单价进行调整，甲种足球的销售单价比上次购买时提高了10％，乙种足球的销售单价比上次购买时降低了10％.如果此次购买甲、乙两种足球的总费用不超过2950元，求这所学校最多可以购买乙种足球的数量.

查看试题解析

28. 下面是小亮学习了“分式方程的应用”后所作的课堂学习笔记，请认真阅读并完成相应的任务．

题目：某商店准备购进甲、乙两种商品，甲种商品每件的进价比乙种商品每件的进价多20元，用2000元购进甲种商品和用1200元购进乙种商品的数量相同．求甲、乙两种商品每件的进价各是多少元．
方法	分析问题	列出方程
解法一	设…… 等量关系：甲商品数量＝乙商品数量	$\frac{2000}{x} = \frac{1200}{x - 20}$
解法二	设…… 等量关系：甲商品进价－乙商品进价＝20	$\frac{2000}{x} - \frac{1200}{x} = 20$

任务：

(1)、解法一所列方程中的x表示，解法二所列方程中的x表示．

A．甲种商品每件进价x元

B．乙种商品每件进价x元

C．甲种商品购进x件

(2)、根据以上解法可求出甲种商品的进价为元/件，乙种商品的进价为元/件．

(3)、若商店将甲种商品每件的售价定为80元，乙种商品每件的售价定为45元．商店计划用不超过1440元的资金购进甲、乙两种商品共40件，当购进的甲、乙两种商品全部售出后，请求出该商店获得最大的利润W ．（利润＝售价－进价）

查看试题解析

29. 醴陵市委市政府顺应百万醴陵人民夙愿，全方位推进“瓷城古韵 $\cdot$ 一江两岸”老城改造，并将其列入十大民生工程项目 $.$ 目前，该项目已完成渌江古桥、状元芳洲、渌江广场、南岸风光带、南街酒吧等建设并投入使用 $.$ 即将启动泗州寺、清代文庙、千年县衙、百年学府门楼、渌水人家等子项目建设 $.$ 醴陵市招投标中心接到甲、乙两个工程队关于清代文庙的投标书，甲、乙工程队施工一天的工程费用分别为 $21$ 万元和 $16$ 万元，市招投标中心根据甲、乙两工程队的投标书测算，应有三种施工方案：
方案一：甲队单独做这项工程刚好如期完成；

方案二：乙队单独做这项工程，要比规定日期多 $5$ 天；

方案三：若甲、乙两队合做 $4$ 天后，余下的工程由乙队单独做，也正好如期完成．

根据以上方案提供的信息，在确保工期不耽误的情况下，你认为哪种方案最节省工程费用，通过计算说明理由．

查看试题解析
30. 【综合与实践】生活中，我们所见到的地面、墙面、服装面料等，上面的图案常常是由一种或几种形状相同的图形拼接而成的.用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，就是平面图形的镶嵌.

(1)、如图1，在 $□ A B C D$ 中， $A B = 2$ ， $A D = 3$ ， $∠ B A D = 60 °$ ，图2右侧的阴影部分可以看成是左侧阴影部分沿射线 $A D$ 方向平移而成，其中，平移的距离是.同理，再进行一次切割平移，可得图3，即图4可以看成由平行四边形经过两次切割平移而成.我们可以用若干个如图4所示的图形，平面镶嵌成如图5的图形，则图5的面积是.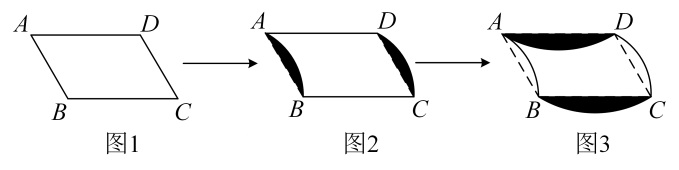

(2)、小明家浴室装修，在墙中央留下了如图6所示的空白，经测量可以按图7所示，全部用边长为1的正三角形瓷砖镶嵌.小明调查后发现：一块边长为1的正三角形瓷砖比一块边长为1的正六边形瓷砖便宜40元；用500元购买正三角形瓷砖与用2500元购买正六边形瓷砖的数量相等。
①请问两种瓷砖每块各多少元？

②小明对比两种瓷砖的价格后发现：用若干块边长为1的正三角形瓷砖和边长为1的正六边形瓷砖一起镶嵌总费用会更少.按小明的想法，将空白处全部镶嵌完，购买瓷砖最少需要元.

查看试题解析