备考2024年中考数学探究性训练专题11 一元二次方程
试卷更新日期:2024-03-24 类型:二轮复习
一、选择题
-
1. 小华仿照探究一元二次方程解的方法,课后尝试探究了一元三次方程的解,列表如下:
x
0
0.5
1
1.5
2
-1
-5.375
-3
6.875
25
据此可知,方程的一个解x的取值范围是( )
A、 B、 C、 D、2. 如图,在一个三角点阵中,从上向下数有无数多行,其中各行点数依次为2,4,6,…,2n,…,请你探究出前n行的点数和所满足的规律.若前n行点数和为930,则n=( )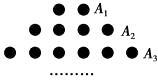
A、29 B、30 C、31 D、323. 小明和小林在探索代数式x2+(x≠0)有没有最大(小)值时,小明做了如下探索:∵x2++2-2 =(x+)2-2≥-2,
∴小明的结论是x2+的最小值为-2
小林做了如下探索
∵x2+-2+2 =(x-)2+2≥2,
小林的结论是x2+的最小值为2;则( )
A、小明正确 B、小林正确 C、小明和小林都正确 D、小明和小林都不正确4. 探讨关于x的一元二次方程总有实数根的条件,下面三名同学给出建议:甲:a,b同号;乙:;丙: . 其中符合条件的是( )A、甲,乙,丙都正确 B、只有甲错误 C、甲,乙,丙都错误 D、只有乙正确5. 我国古代数学家研究过一元二次方程(正根)的几何解法.以方程x2+5x﹣14=0,即x(x+5)=14为例说明,《方图注》中记载的方法是:构造图(如图)中大正方形的面积是(x+x+5)2 , 同时它又等于四个矩形的面积加上中间小正方形的面积,即4×14+52 , 因此x=2.则在下面构图中,能正确说明方程x2﹣3x﹣10=0的构图是( )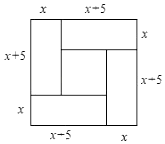 A、
A、 B、
B、 C、
C、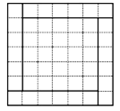 D、
D、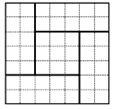 6. 小宁在研究关于x的一元二次方程x2-4x+m=0时,得到以下4个结论:
6. 小宁在研究关于x的一元二次方程x2-4x+m=0时,得到以下4个结论:①若m=4,则方程有两个相等的实数根;②若m<0,则方程必有两个异号的实数根;③若m<4,则方程的两个实数根不可能都大于2;④若m<-5,则方程的两个实数根一个小于5,另一个大于5.其中结论正确的个数有( )
A、1个 B、2个 C、3个 D、4个7. 已知实数 ,现有甲、乙、丙、丁四人对关于 的方程 进行了讨论:甲说:这一定是关于 的一元二次方程;
乙说:这有可能是关于 的一元一次方程;
丙说:当 时,该方程有实数根;
丁说:只有当 且 时,该方程有实数根.( )
A、甲和丙说的对 B、甲和丁说的对 C、乙和丙说的对 D、乙和丁说的对8. 伊斯兰数学家塔比·伊本·库拉( Thabit ibn Qurra,830-890)在其著作《以几何方法证明代数问题》中讨论了二次方程的几何解法。例如:可以用如图来解关于x的方程 ,其中ABFE为长方形,ABCD为正方形,且DE=m,BF×CD=n,则方程 的其中一个正根为( ) A、DE的长 B、AB的长 C、AE的长 D、BE的长
A、DE的长 B、AB的长 C、AE的长 D、BE的长二、填空题
-
9. 小亮在计算的值时,把的值看错了,其结果等于25,细心的小敏把正确的的值代入计算, 其结果也是25.为了探究明白,她又把代入,结果还是25.则的值为 .10. 某校“自然之美”研究小组在野外考察时发现一种植物的生长规律,即植物的1个主干上长出x个枝干,每个枝干又长出x个小分支,现在一株植物上有主干、枝干、小分支数量之和为73,根据题意,请列出方程为11. 我们古代数学家研究过一元二次方程.下面是我国南宋数学家杨辉在1275年提出的一个问题:“直田积(矩形面积)八百六十四步(平方步),只云阔(宽)不及长一十二步(宽比长少一十二步),问阔及长各几步.”意思是一块田是矩形,矩形面积为 , 长比宽多 , 如果设宽为 , 则列出的方程为 .12. 形如 的方程可用如图所示的图解法研究:画 ,使 , , ,再在斜边 上截取 ,则可以发现该方程的一个正根是线段的长.
 13. 你知道吗,对于一元二次方程,我国古代数学家还研究过其几何解法呢!以方程即为例加以说明.数学家赵爽(公元世纪)在其所著的《勾股圆方图注》中记载的方法是:构造图(如下面左图中)大正方形的面积是 , 其中它又等于四个矩形的面积加上中间小正方形的面积,即 , 据此易得那么在下面右边三个构图(矩形的顶点均落在边长为1的小正方形网格格点上)中,能够说明方程的正确构图是.(只填序号).
13. 你知道吗,对于一元二次方程,我国古代数学家还研究过其几何解法呢!以方程即为例加以说明.数学家赵爽(公元世纪)在其所著的《勾股圆方图注》中记载的方法是:构造图(如下面左图中)大正方形的面积是 , 其中它又等于四个矩形的面积加上中间小正方形的面积,即 , 据此易得那么在下面右边三个构图(矩形的顶点均落在边长为1的小正方形网格格点上)中,能够说明方程的正确构图是.(只填序号).
 14. 古代丝绸之路上的花剌子模地区曾经诞生过一位伟大的数学家-“代数学之父”阿尔·花拉子米.在研究一元二次方程解法的过程中,他觉得“有必要用几何学方式来证明曾用数字解释过的问题的符合题意性”.
14. 古代丝绸之路上的花剌子模地区曾经诞生过一位伟大的数学家-“代数学之父”阿尔·花拉子米.在研究一元二次方程解法的过程中,他觉得“有必要用几何学方式来证明曾用数字解释过的问题的符合题意性”.
以 为例,花拉子米的几何解法如下:
如图,在边长为 的正方形的两个相邻边上作边长分别为 和5的矩形,再补上一个边长为5的小正方形,最终把图形补成一个大正方形.

通过不同的方式来表达大正方形的面积,可以将原方程化为(x+ )2=39+ , 从而得到此方程的正根是 .
三、理论探究题
-
15. 阅读材料:
解方程: . 我们可以将视为一个整体,然后设 , 则 , 原方程化为①,解得 .
当时, .
当时, .
原方程的解为 .
根据上面的解答,解决下面的问题:
(1)、填空:在由原方程得到方程①的过程中,利用法达到降次的目的,体现了的数学思想;(2)、解方程; .16. 仔细阅读下列解题过程:若 , 求 的值.
解: ,
,
,
,
.
根据以上解题过程, 试探究下列问题:
(1)、若 , 求 的值.(2)、若 , 求 的值.17. 阅读材料:若 , 求、的值.解:∵
∴ .
根据你的观察,探究下面的问题:
(1)、已知 , 求的值;(2)、已知等腰的三边长、、都是正整数,且满足 , 求的周长;(3)、已知 , 求的值.18. 某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:对于三个实数 , , , 用表示这三个数的平均数,用表示这三个数中最小的数,例如: .
请结合上述材料,解决下列问题:(1)、 ;
(2)、若 , 求的值;
(3)、若 , 且点 , 在反比例函数的图象上,求的值.19. 阅读材料:若 ,求m、n的值.解: ,
,
,
.
根据你的观察,探究下面的问题:
(1)、已知 ,求 的值.(2)、已知△ABC的三边长a、b、c都是正整数,且满足 ,求边c的最大值.(3)、若已知 ,求 的值20. 关于x的一元二次方程经过适当变形,可以写成的形式.现列表探究的变形:变形
s
t
p
-1
5
0
0
4
5
1
q
8
2
2
9
回答下列问题:
(1)、表格中q的值为 .(2)、观察上述探究过程,表格中s与t满足的等量关系为 .(3)、记的两个变形为和 , 求的值.21. 综合与探究:如果关于x的一元二次方程有两个实数根,且其中一个根比另一个根大1,那么称这样的方程是“邻根方程”.例如:一元二次方程的两个根是 , , 则方程:是“邻根方程”.(1)、通过计算,判断下列方程是否是“邻根方程”:①;② .
(2)、已知关于x的一元二次方程(m是常数)是“邻根方程”,求m的值.22. 著名数学家高斯曾说过:“如果别人思考数学的真理像我一样深入持久,他也会找到我的发现”,我们向伟人看齐,将这种勤思善学、砺能笃行的精神运用于日常的数学学习中来,尝试发现新的惊喜.【提出问题】
我们曾探究过一元二次方程根与系数的关系,如果一元二次方程的系数按照某种规律发生变化,原方程的根与新方程的根是否也会产生某种联系?
【构造关系】
将一元二次方程的二次项系数、一次项系数和常数项按照的比例放大或缩小,其中 , 我们称新方程为原方程的“系变方程”,系变倍数为.
(1)、当系变倍数为3时,求解一元二次方程的“系变方程”.(2)、【自能探究】已知某一元二次方程有两个实数根 , , 当时,其“系变方程”也有两个实数根、 , 且 , 求的最小值.(3)、已知关于的方程有四个实数根、、、 , 问是否存在定值 , 对于任意实数 , 都满足 , 若存在,请求出的值.若不存在,请说明理由.四、数形结合探究题
-
23. 在学习多边形的相关知识时,小张同学和小王同学对老师布置“探究多边形的对角线条数”的作业很盛兴趣,小张同学探究得到了边形的对角线条数的公式,并通过上网查证自己探究的结论是正确的.下图是两位同学进行交流的情景.

小王同学把哪个多边形对角线的条数数错了?请你通过计算或者画图来说明.
24. 阅读探究:任意给定一个矩形 , 是否存在另一个矩形 , 它的周长和面积分别是已知矩形周长和面积的一半。(1)、当已知矩形的相邻两边的长分别为6和1时,小亮同学是这样研究的:设所求矩形的相邻两边的长分别是和 , 由题意得方程组 , 消去 , 化简 , , , , 所以存在满足要求的矩形;(2)、如果已知矩形的相邻两边的长分别为2和1,请你仿照小亮的方法研究是否存在满足要求的矩形;(3)、如果矩形的相邻两边的长分别为和 , 请你研究满足什么条件时,矩形存在.25. 下面是小李探索 的近似值的过程:我们知道面积是2的正方形的边长是 ,易知 >1,因此可设 ,可画出如下示意图. 由图中面积计算, S正方形= ,另一方面由题意知S正方形= ,所以 略去 ,得方程 ,解得 ,即 ,仿照上述方法,探究 的近似值(画出示意图,标明数据,并写出求解过程)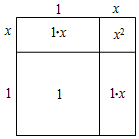
五、实践探究题
-
26. 根据以下素材,探索完成任务
如何设计纸盒
素材1
利用一边长为40cm的正方形纸板可能设计成如图1和图2所示的两种纸盒,图1是无盖的纸盒,图2是一个有盖的纸盒.

素材2
如图,若在正方形硬纸板的四角各剪掉一个同样大小的小正方形,将剩余部分折成一个无盖的长方体盒子。

问题解决
任务1
初步探究:折一个底面积为无盖长方体盒子
求剪掉的小正方形的边长为多少?
任务2
探究折成的无盖长方体盒子的侧面积是否有最大值?
如果有,求出这个最大值和此时剪掉的小正方形的边长;如果没有,说明理由
27. 根据以下提供的素材,完成任务。如何制定商店的销售定价方案
根据以下商店提供的信息,请你设计一个合适的商品定价方案。
素材一
1.商品成本:100元/件,每天进货120件,并且全部卖出.
2.商品有A、B两种包装,目前的售价和日销售量如下表:
A包装
B包装
售价(元/件)
112
108
日销售量(件)
40
80
素材二
为了增加盈利,该商店准备降低A包装商品的售价,同时提高B包装商品的售价,通过市场调研发现,在一定范围内,A包装商品售价每降低1元可多卖出2件,B包装商品售价每提高1元就少卖出2件.商店发现若按照当前的总销量销售A,B两种包装商品,最大总利润为1264元.
素材三
销售一段时间后,商店发现若减少A,B两种包装商品的总销量。A,B两种包装商品的销售总利润反而有所增长.为进一步增加盈利,商店决定将A,B两种包装商品的总销量减少10件.
问题解决
任务一
探究商品销量
设每件A包装商品售价降低元(为整数),用含的代数式表示降价后A包装商品每日的总销售最为 ▲ 件.
任务二
探究商品售价
在每日A,B两种包装商品的总销量为120件的前提下,为使总利润达到最大,试求出此时A,B两种包装商品的售价.
任务三
确定定价方案
请设计一种A,B两种包装商品的定价方案,使一天的销售总利润超过1430元.(直接写出方案即可)
28. 根据以下素材,探索完成任务.如何设计实体店背景下的网上销售价格方案?
素材1
某公司在网上和实体店同时销售一种自主研发的小商品,成本价为40元/件.
素材2
该商品的网上销售价定为60元/件,平均每天销售量是200件,在实体店的销售价定为80元/件,平均每天销售量是100件.按公司规定,实体店的销售价保持不变,网上销售价可按实际情况进行适当调整,需确保网上销售价始终高于成本价.
素材3
据调查,网上销售价每降低1元,网上销售每天平均多售出20件,实体店的销售受网上影响,平均每天销售量减少2件.
问题解决
任务1
计算所获利润
当该商品网上销售价为50元/件时,求公司在网上销售该商品每天的毛利润与实体店销售该商品每天的毛利润各是多少元?
任务2
拟定价格方案
公司要求每天的总毛利润((总毛利润=网上毛利润+实体店毛利润)达到8160元,求每件商品的网上销售价是多少元?
任务3
探究最大利润
该商品的网上销售价每件▲ 元时,该公司每天销售这种小商品的总毛利润最大.
29. 综合实践:项目主题
“亚运主题”草坪设计
项目情境
为了迎亚会,同学们参与一块长为40米,宽为30米的矩形“亚运主题”草
坪方案设计的项目学习.以下为项目学习小组对草坪设计的研究过程.
活动任务一
请设计两条相同宽度的小路连接矩形草坪两组对边.小组内同学们设计的方案主要有甲、乙、丙、丁四种典型的方案

驱动问题一
(1)项目小组设计出来的四种方案小路面积的大小关糸?
①直观猜想:我认为 ▲ ;(请用简洁的语言或代数式表达你的猜想)
②具体验证:选择最简单的甲、乙方案,假设小路宽为1米,则甲、乙方案中小路的面积分别为 ▲ 和 ▲ ;
③一般验证:若小路宽为x米,则甲、乙方案中小路所占的面积分别为 ▲ 和 ▲ .
活动任务二
为施工方便,学校选择甲种方案设计,并要求除小路后草坪面积约为1064平方米.
驱动问题二
(2)请计算两条小路的宽度是多少?
活动任务三
为了布置五环标志等亚运元素,将在草坪上的亚运宣传主题墙前,用篱笆围(三边)成面积为100平方米的矩形 , 如图.
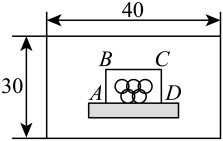
驱动问题三
(3)为了使篱笆恰好用完同时围住三面,项目小组的同学对下列问题展开探究,其中矩形宽 , 长 .
①若30米长的篱笆,请用两种不同的函数表示y关于x的函数关系.
②数学之星小明提出一个问题:若a米长的篱笆恰好用完,且有两种不同方案可以选择,使得两种方案的宽之和小于15米,甲同学说“篱笆的长可以是28米”,乙同学说“篱笆的长可以是32米”,你认为他们俩的说法对吗?请说明理由.