备考2024年中考数学探究性训练专题8 一元一次方程
试卷更新日期:2024-03-24 类型:二轮复习
一、选择题
-
1. 如图,表中给出的是某月的月历,任意选取“H”型框中的7个数(如阴影部分所示),请你运用所学的数学知识探究,这7个数的和不可能是( )
 A、168 B、140 C、98 D、632. 幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”中,把“洛书”用今天的数学符号翻译出来,就是一个三阶幻方.请你探究如图洛书三阶幻方中,奇数和偶数的位置、数和数之间的数量关系所呈现的规律,根据这一规律,求出 , , 则( )
A、168 B、140 C、98 D、632. 幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”中,把“洛书”用今天的数学符号翻译出来,就是一个三阶幻方.请你探究如图洛书三阶幻方中,奇数和偶数的位置、数和数之间的数量关系所呈现的规律,根据这一规律,求出 , , 则( )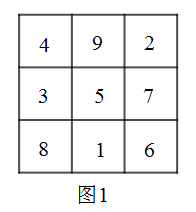
 A、16 B、8 C、 D、3. 观察下列两行数:
A、16 B、8 C、 D、3. 观察下列两行数:1,3,5,7,9,11,13,15,17,19,…
1,4,7,10,13,16,19,22,25,28,…
探究发现:第1个相同的数是1,第2个相同的数是7,…,若第n个相同的数是103,则n等于( )
A、17 B、18 C、19 D、20二、填空题
-
4. 甲乙二人在环形跑道上同时同地出发,同向运动.若甲的速度是乙的速度的2倍,则甲运动2周,甲、乙第一次相遇;若甲的速度是乙的速度3倍,则甲运动 周,甲、乙第一次相遇;若甲的速度是乙的速度4倍,则甲运动 周,甲、乙第一次相遇,…,以此探究正常走时的时钟,时针和分针从0点(12点)同时出发,分针旋转周,时针和分针第一次相遇.
三、理论探究题
-
5. 用※定义一种新运算:对于任意有理数a和b , 规定a※b=ab2+2ab+a , 如1※2=1×22+2×1×2+1=9(1)、求(﹣4)※3;(2)、若※3=﹣16,求a的值.6. 阅读下面的解题过程:
解方程:|x+3|=2.
解:当x+3≥0时,原方程可化成为x+3=2
解得x=﹣1,经检验x=﹣1是方程的解;
当x+3<0,原方程可化为,﹣(x+3)=2
解得x=﹣5,经检验x=﹣5是方程的解.
所以原方程的解是x=﹣1,x=﹣5.
解答下面的两个问题:
(1)解方程:|3x﹣2|﹣4=0;
(2)探究:当值a为何值时,方程|x﹣2|=a,
①无解;②只有一个解;③有两个解.
7. 阅读下列材料:问题:怎样将表示成分数?
小明的探究过程如下:
设①,
②,
③,
④,
⑤,
⑥,
⑦.
根据以上信息,回答下列问题:
(1)、从步骤①到步骤②,变形的依据是 , 从步骤⑤到步骤⑥,变形的依据是.(2)、仿照上述探究过程,请你将表示成分数的形式.8. 定义:对任意一个两位数 , 如果满足个位数字与十位数字互不相同,且都不为零那么称这个两位数为“互异数”.将一个“互异数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与11的商记为 . 例如: , 对调个位数字与十位数字得到新两位数21,新两位数与原两位数的和为 , 和与11的商为 , 所以 . 根据以上定义,回答下列问题:(1)、①下列两位数:50,44,35中,“互异数”为;②计算:;(2)、一个“互异数”的十位数字是 , 个位数字是 , 且 , 求的值;(3)、如果一个“互异数”的十位数字是 , 个位数字是 , 且 , 求“互异数”的值.9. 用“☆”定义一种新运算:对于任意有理数a和b,规定 , 如: .(1)、求的值;(2)、若 , 求a的值;(3)、若 , (其中x为有理数),试比较与n的大小.10. 综合与实践阅读材料,解答下列问题:
幻方历史悠久,传说最早出现在夏禹时代的“洛书”,如图1.把图1的洛书用今天的数学符号翻译出来,就是一个三阶幻方,如图2,它的每行、每列、每条对角线上的三个数的和都相等.
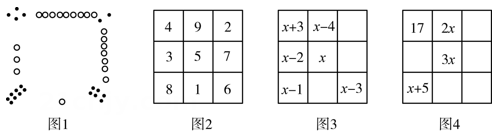 (1)、在图2中,每行、每列、每条对角线上三个数的和都是;(2)、设图3所示的三阶幻方中间的数为x(x为整数),请用含x的代数式将图3幻方补充完整;(3)、如图4是一个三阶幻方,按方格中已给的信息,求x的值.11. 一般情况不成立,但有些数可以使得它成立,例如:.我们称使得成立的一对数为“相伴数对”,记为.(1)、若是“相伴数对”,求值;(2)、若是“相伴数对”,求代数式的值。12. 阅读材料:
(1)、在图2中,每行、每列、每条对角线上三个数的和都是;(2)、设图3所示的三阶幻方中间的数为x(x为整数),请用含x的代数式将图3幻方补充完整;(3)、如图4是一个三阶幻方,按方格中已给的信息,求x的值.11. 一般情况不成立,但有些数可以使得它成立,例如:.我们称使得成立的一对数为“相伴数对”,记为.(1)、若是“相伴数对”,求值;(2)、若是“相伴数对”,求代数式的值。12. 阅读材料:我们定义:如果两个实数的和等于这两个实数的积,那么这两个实数就叫做“和积等数对”,即:如果 , 那么a与b就叫做“和积等数对”,记为.
例如: , , ,
则称数对 , , 是“和积等数对”.
根据上述材料,解决下列问题:
(1)、下列数对中,“和积等数对”是 填序号;①; ②; ③.
(2)、如果是“和积等数对”,请求出x的值;(3)、如果是“和积等数对”,那么m=(用含的代数式表示).13. 探究题:阅读下列材料,规定一种运 , 例如 , 再如 , 按照这种运算的规定,请解答下列问题:(1)、 . (只填结果);(2)、若 , 求的值.(写出解题过程)(3)、若化简后是一个关于x的一元一次方程,求k的值.(写出解题过程)14. 新定义题小明在课外阅读中对有关“自定义型题”有了一定的了解,他也尝试着自定义了“颠倒数”的概念:从左到右写下一个自然数,再把它按从右到左的顺序写一遍,如果两数位数相同,这样就得到了这个数的“颠倒数”,如286的颠倒数是682.请你探究,解决下列问题:
(1)、请直接写出2019的“颠倒数”为.(2)、能否找到一个数字填入空格,使下列由“颠倒数”构成的等式成立?□ □ 。请你用下列步骤探究:
设这个数字为 ,将自然数“6□”和“□6”转化为用含 的代数式表示分别为和;
列出关于 的满足条件的方程:;
解这个方程得: ;
经检验,所求 的值符合题意吗?(填“符合”或“不符合”)
15. 定义:如果两个一元一次方程的解之和为 , 我们就称这两个方程互为“阳光方程”例如:的解为 , 的解为 , 所以这两个方程互为“阳光方程”.(1)、若关于的一元一次方程与是“阳光方程”,则 .(2)、已知两个一元一次方程互为“阳光方程”,且这两个“阳光方程”的解的差为若其中一个方程的解为 , 求的值.(3)、已知关于的一元一次方程的解是 , 请写出解是的关于的一元一次方程:只需要补充含有的代数式 .若关于的一元一次方程和互为“阳光方程”,则关于的一元一次方程的解为 .
16. 【实验与探究】根据教材“将无限循环小数化为分数”材料,并解决相应问题:我们知道分数写为小数形式即为 , 反之,无限循环小数写成分数形式即.一般地,任何一个无限循环小数都可以写成分数形式吗?如果可以,应怎样写呢?
【发现】先以无限循环小数为例进行讨论.
设 , 由可知, , 即.解方程 , 得.于是.
【类比探究】再以无限循环小数为例,做进一步的讨论.
无限循环小数 , 它的循环节有两位,类比上面的讨论可以想到如下做法.
设 , 由可知,所以.解方程,得 , 于是得
【解决问题】
(1)、请你把以下无限小数写成分数形式,;;(2)、根据以上过程比较与1的大小关系,并说明你的理由。17. 我们规定,若关于的一元一次方程的解为 , 则称该方程为“天心方程”.例如,的解为 , 而 , 则该方程就是“天心方程”.请根据上述规定解答下列问题:(1)、一元一次方程(填“是”或“不是”) “天心方程”.(2)、若关于的一元一次方程是“天心方程”,则 .(3)、若关于的一元一次方程是“天心方程”,且它的解为 , 求的值.(4)、若关于的一元一次方程和关于的一元一次方程都是“天心方程”,求代数式的值.18. “数形结合”是一种非常重要的数学思想,它可以把抽象的数量关系与直观的几何图形结合起来解决问题.(1)、探究:方程 , 可以用两种方法求解,将探究过程补充完整.方法一当时,;
当时,=2.
方法二的意义是数轴上表示x的点与表示的点之间的距离是2.
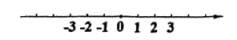
上述两种方法,都可以求得方程的解是.
(2)、应用:根据探究中的方法,求得方程的解是.(3)、拓展:方程的解是.19. 阅读下列材料并解决有关问题:知道: 现在我们可以用这一结论来化简含有绝对值的代数式,
如化简代数式时,可令和 , 分别求得 , (称 , 分别为与的零点值).在有理数范围内,零点值和,可将全体有理数分成不重复且不遗漏的如下种情况:()() () . 从而化简代数式可分以下种情况:(1)当时,原式(2)当时,原式;(3)当时,原式 . 综上所述,原式
通过以上阅读,请你解决以下问题:
(1)、分别求出和的零点值;(2)、化简代数式;(3)、求方程:的整数解;20. 定义:关于x的方程与方程(a,b均为不等于0的常数)互为“反对方程”例如:方程与方程互为“反对方程”.
(1)、若方程与方程互为“反对方程”,则 .(2)、若关于x的方程与方程互为“反对方程”,求m,n的值.(3)、若关于x的方程与其“反对方程”的解都是整数,求常数b的值.21. 定义:如果两个一元一次方程的解之和为1,我们就称这两个方程为“美好方程”.例如:方程4x=8和x+1=0为“美好方程”.(1)、若关于x的方程3x+m=0与方程4x-2=x+10是“美好方程”,求m的值;(2)、若“美好方程”的两个解的差为8,其中一个解为n , 求n的值;(3)、若关于x的一元一次方程和是“美好方程”,求关于y的一元一次方程的解.四、数形结合探究题
-
22. 操作探究:已知在纸面上有一数轴(如下图所示)左右折叠纸面,折痕所在的直线与数轴的交点为“对折中心点”.
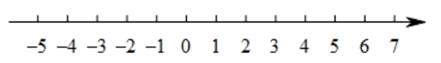 (1)、操作一:
(1)、操作一:左右折叠纸面,使表示1的点与表示-1的点重合,则表示-3的点与表示的点重合;
(2)、操作二:左右折叠纸面,使表示-1的点与表示3的点重合,回答以下问题:
①“对折中心点”所表示的数为 , 对折后表示5的点与表示的点重合;
②若数轴上 , 两点之间的距离为12( 在 的左侧),且 , 两点经折叠后重合,则 点表示的数是 , 点表示的数是 .
23. 综合与探究数轴是一个非常重要的数学工具,它使数和数轴上的点建立起一一对应的关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.小明在一条长方形纸带上画了一条数轴,进行如下操作探究:
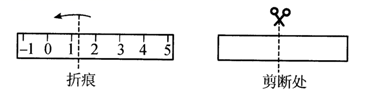 (1)、操作1:折叠纸带,使数轴上表示 的点与表示 的点重合,则表示数 的点与表示数的点重合.(2)、操作2:折叠纸带,使数轴上表示 的点与表示 的点重合,则表示 的点与表示数的点重合.(3)、操作3:如图,在数轴上剪下6个单位长度(从 到5)的一条线段,并把这条线段沿某点向左折叠,然后在重叠部分的某处剪一刀得到三条线段,发现这三条线段的长度之比为1:1:2,则折痕处对应的点表示的数可能是几?24. 如图
(1)、操作1:折叠纸带,使数轴上表示 的点与表示 的点重合,则表示数 的点与表示数的点重合.(2)、操作2:折叠纸带,使数轴上表示 的点与表示 的点重合,则表示 的点与表示数的点重合.(3)、操作3:如图,在数轴上剪下6个单位长度(从 到5)的一条线段,并把这条线段沿某点向左折叠,然后在重叠部分的某处剪一刀得到三条线段,发现这三条线段的长度之比为1:1:2,则折痕处对应的点表示的数可能是几?24. 如图
【问题提出】已知∠BOC与∠AOC有共同的始边OC,且满足∠BOC=2∠AOC,若∠AOC=28°,求∠AOB的度数.
【问题解决】圆圆首先画出两个符合题意的图形,运用分类讨论的数学思想,解决问题.
在图①中,当射线OA在∠BOC的内部时,由题意易得∠AOB=28°;
在图②中,当射线OA在∠BOC的外部时,由题意易得∠AOB=84°.
【问题应用】请仿照这种方法,解决下面两个问题
(1)、如图③,已知点A,B,C在数轴上对应的数分别为﹣4,2,1,请在数轴上标出线段AC的中点D并写出D所表示的数;若数轴上存在点E,它到点C的距离恰好是线段AB的长,求线段DE的长.(2)、如果两个角的差的绝对值等于90°,就称这两个角互为垂角,例如:∠1=120°,∠2=30°,|∠1﹣∠2|=90°,则∠1和∠2互为垂角(本题中所有角都是指大于0°且小于180°的角).①若∠α=140°,求∠α的垂角;②如果一个角的垂角等于这个角的补角的 , 求这个角的度数.
25. 某实践小组设计宣传牌:
如图1是长方形宣传牌,长 , 宽 , 中间可以用来设计的部分是长方形 , 且 . 四周空白部分的宽度相等,设四周宽度为;
如图2,为了美观,将长方形分割成大小相等的左、中、右三个小长方形栏目,栏目与栏目之间的中缝间距相等;
如图3,每个栏目划出8个小正方形方格,中间有十字间隔,竖行两列中间间隔和横向中间间隔宽度比为 .
(1)、 , (用含的代数式表示);(2)、求出图1四周宽度的值;(3)、求每个栏目的水平宽度;(4)、求栏目与栏目之间中缝的间距.五、实践探究题
-
26. 在学习“一元一次方程的应用”时.小明和小天在一起讨论下列问题:
某汽车队运送一批援助物资.若每辆车装吨,还剩下吨未装;若每辆车装吨,则最后一辆车还能装吨.这个车队有多少辆车?
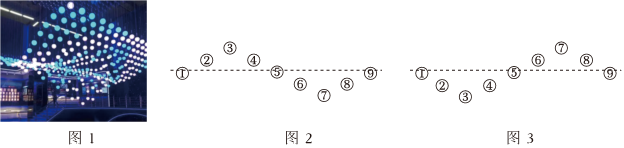
(1)、若设这个车队有辆车,根据两种装车方案中援助物资的总量不变,请列出方程并解答.(2)、小明和小天讨论后,觉得也可以设这批援助物资有吨,根据两种装车方案中车辆数不变来列方程,请判断他们的说法是否正确,若正确,按这种方法列出方程并进行解答.27. 列方程解应用题:为了丰富社会实践活动,引导学生科学探究.学校组织七年级同学走进中国科技馆.亲近科学,感受科技魅力,来到科技馆大厅,同学们就被大厅里会“跳舞”的“小球矩阵”吸引住了(如图1).白色小球全部由计算机精准控制,每一只小球可以“悬浮”在大厅上空的不同位置,演绎着曲线、曲面、平面、文字和三维图案等各种动态造型.
已知每个小球分别由独立的电机控制.图2,图3分别是9个小球可构成的两个造型,在每个造型中,相邻小球的高度差均为a米.为了使小球从造型一(如图2)变到造型二(如图3),控制电机使造型一中的②,③,④,⑥,⑦,⑧号小球同时运动,②,③,④小球向下运动,运动速度均为4米/秒;⑥,⑦,⑧号小球向上运动,运动速度均为3米/秒.当每个小球到达造型二的相应位置时就停止运动.已知⑦号小球比②号小球晚秒到达相应位置,问②号小球运动了多少米?
 28. 数学活动-探究日历中的数字规律
28. 数学活动-探究日历中的数字规律如图1是2022年2月份的日历,小宇在其中画出两个2×2的方框,每个框均框住位置为
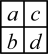 的四个数,计算“bc-ad”的值,探索其运算结果的规律.
的四个数,计算“bc-ad”的值,探索其运算结果的规律.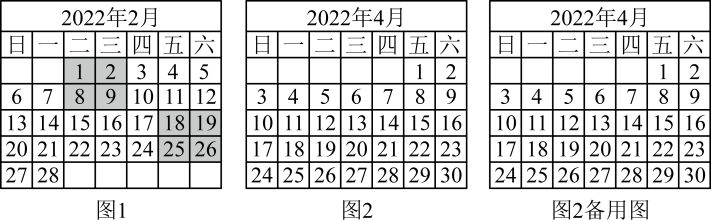 (1)、计算:2×8-1×9= , 19×25-18×26=.(2)、小宇通过特例分析,猜想所有日历中,2×2方框里“bc-ad”的结果都不变,并说明理由如下,请你将其过程补充完整;
(1)、计算:2×8-1×9= , 19×25-18×26=.(2)、小宇通过特例分析,猜想所有日历中,2×2方框里“bc-ad”的结果都不变,并说明理由如下,请你将其过程补充完整;解:bc-ad的值均为 ▲ . 理由如下:
设a=x,则b=x+7,c=x+1,d= ▲
因为bc-ad= ▲
所以bc-ad的值均为 ▲
(3)、同学们利用小宇的方法,借助2022年4月份的日历,继续进行如下探究.请从下列A,B两题中任选一题作答.我选择 ▲
A,在日历中用“十字框”框住位置为
 的五个数,探究bc-ad的值的规律,请写出你的结论,并说明理由.
的五个数,探究bc-ad的值的规律,请写出你的结论,并说明理由.B.在日历中用日数柜框住位置为
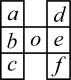 的七个数,探究bc-ad的值的规律,请写出你的结论,并说明理由.29. 为激发学生们对科技的好奇心和探索欲,培养学生的创新意识和创新精神,某学校开展了“智能小车实验探究”活动.某小组观察探究小车运动中的函数关系,如图,在一条长为的水平直线轨道上,放置一辆长为的智能小车,开始时小车左端与处挡板重合,然后以的速度匀速向右行驶,当小车接触到处的挡板时因为要改变方向需停顿 , 然后以相同的速度返回,至再次与处的挡板接触时小车停止运动.在这个过程中,设小车的右端与处挡板的距离为 , 小车出发后的时间为 , 请根据所给条件解决下列问题:
的七个数,探究bc-ad的值的规律,请写出你的结论,并说明理由.29. 为激发学生们对科技的好奇心和探索欲,培养学生的创新意识和创新精神,某学校开展了“智能小车实验探究”活动.某小组观察探究小车运动中的函数关系,如图,在一条长为的水平直线轨道上,放置一辆长为的智能小车,开始时小车左端与处挡板重合,然后以的速度匀速向右行驶,当小车接触到处的挡板时因为要改变方向需停顿 , 然后以相同的速度返回,至再次与处的挡板接触时小车停止运动.在这个过程中,设小车的右端与处挡板的距离为 , 小车出发后的时间为 , 请根据所给条件解决下列问题: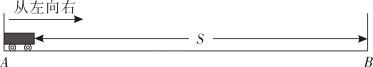 (1)、小车运动时间为时,的值为;(2)、小车从处驶向处的过程中,求与的函数表达式;(3)、当小车左端与处挡板的距离比小车右端与处挡板距离的2倍多时,请求出的值.30. 请看“计算框图”,计算框图中有很多的规范要求:“输入输出框”用“
(1)、小车运动时间为时,的值为;(2)、小车从处驶向处的过程中,求与的函数表达式;(3)、当小车左端与处挡板的距离比小车右端与处挡板距离的2倍多时,请求出的值.30. 请看“计算框图”,计算框图中有很多的规范要求:“输入输出框”用“ ”表示(表示输入、输出操作);“处理框”用“
”表示(表示输入、输出操作);“处理框”用“ ”表示(表示数据处理和运算);“判断框”用“
”表示(表示数据处理和运算);“判断框”用“ ”表示(根据条件决定执行两条路径中的某一条)
”表示(根据条件决定执行两条路径中的某一条)
价目表
每月用水量
单价
不超出15吨的部分
3元/吨
超15吨不超25吨的部分
4元/吨
超出25吨的部分
6元/吨
注:水费按月结算
(1)、【观察与思考】:①在图1中写出操作过程.
(2)、【类比与归纳】:①如图2,如果输入的值为 , 那么输出的结果为 .
②根据图3所示的计算程序,若输出的值 , 则输入的值
(3)、【生活与应用】:为加强居民节水意识,东阳市决定对居民用水实行“阶梯价”,见价目表.
问题①:若该居民1月用水量不超25吨,请你设计“计算框图”,使得输入数据为用水量 , 输出数为水费 .
问题②:若该居民2、3月份共用水34吨(3月份用水超过2月份),共交水费118元,则该居民2、3月份各用水多少吨?
-