【培优卷】2024年北师大版数学八（下）第四章因式分解章末检测

试卷更新日期：2024-03-24 类型：单元试卷

进入出卷网下载

一、选择题（每题2分，共20分）

1. 使用提公因式法分解 $4 a^{2} b - 6 a b^{2} + 2 a^{3} b^{3}$ 时，公因式是（）

A、 $12 a^{3} b^{3}$ B、 $2 a^{3} b^{3}$ C、2ab D、 $4 a^{2} b$

查看试题解析
2. 解方程（x-1）²-3（x-1）＝0的最适当的方法是（　　）

A、直接开平方法 B、配方法 C、公式法 D、因式分解法

查看试题解析
3. 下列等式从左到右的变形是因式分解的是（）

A、 $x^{2} - x + 1 = x (x - 1) + 1$ b B、 $(2 x + 3 y) (2 x - 3 y) = 4 x^{2} - 9 y^{2}$ C、 $x^{2} + y^{2} = (x + y)^{2} - 2 x y$ D、 $x^{2} + 6 x + 9 = (x + 3)^{2}$

查看试题解析
4. 给出下列各式： $x^{2} - y^{2}$ ， $- x^{2} + y^{2}$ ， $(- x)^{2} + (- y)^{2}$ ， $- x^{2} - y^{2}$ ， $x^{4} - y^{4}$ ，其中能用平方差公式进行因式分解的有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
5. 下列各多项式中，能运用公式法分解因式的有（）

A、 $4 x^{2} + 1$ B、 $9 a^{2} b^{2} - 3 a b + 1$ C、 $- x^{2} - y^{2}$ D、 $x^{2} - x + \frac{1}{4}$

查看试题解析
6. 下列从左到右的变形是因式分解且分解正确的是（）

A、 $(x + 2 y) (x - 2 y) = x^{2} - 4 y^{2}$ B、 $x^{2} + 2 x + 1 = x (x + 2) + 1$ C、 $4 x^{2} + 8 x + 4 = 4 (x^{2} + 2 x + 1)$ D、 $- 8 x^{2} + 8 x - 2 = - 2 (2 x - 1)^{2}$

查看试题解析
7. 计算：2¹¹﹣2¹⁰的结果是（　　）

A、﹣2¹⁰ B、2 C、-2 D、2¹⁰

查看试题解析
8. 若n为大于3的整数，则n³-3n²+2n（）

A、能被3整除不一定能被6整除 B、能被6整除不一定能被12整除 C、能被12整除不一定能被24整除 D、以上说法都不对

查看试题解析
9. 多项式 $x^{2} + 5 x - 14$ 可因式分解成 $(x + a) (b x + c)$ ，其中 $a$ 、 $b$ 、 $c$ 均为整数，求 $a + 2 c$ 的值为（）

A、-12 B、3 C、-3或12 D、3或12

查看试题解析
10. 小林是一位密码编译爱好者，在他的密码手册中有这样一条信息： $x - 1 ，$ $a - b ，$ 3， $x^{2} + 1 ，$ $a ，$ $x + 1$ 分别对应六个字：国，爱，我，数，学，祖，现将 $3 a (x^{2} - 1) - 3 b (x^{2} - 1)$ 因式分解，结果呈现的密码信息可能是（）

A、我爱数学 B、爱祖国 C、祖国数学 D、我爱祖国

查看试题解析

二、填空题（每题3分，共15分）

11. 已知 $m n = 2$ ， $n + m = 3$ ，则 $m^{2} n + m n^{2} =$ ．

查看试题解析
12. 分解因式： $b^{4} - b^{2} - 12 =$

查看试题解析
13. 分解因式（xy﹣1）²﹣（x+y﹣2xy）（2﹣x﹣y）= ．

查看试题解析
14. 因式分解2x²- 12x +18的结果是

查看试题解析
15. 若m+n＝2，mn＝1，则m³n+mn³+2m²n²＝．

查看试题解析

三、计算题（共2题，共18分）

16. 选取最恰当的方法解方程：

(1)、 $(x - 3)^{2} = 5 (3 - x)$ ；

(2)、 $3 x^{2} - 6 x = 48$ ．

查看试题解析
17. 把下列各式因式分解:

(1)、(a²-4)²+6(a²-4)+9;

(2)、(x²+16y²)²-64x²y²;

(3)、a³-a+2b-2a²b;

(4)、x²-2xy+y²+2x-2y+1.

查看试题解析

四、解答题（共10题，共67分）

18. 已知 $x$ ， $y$ ， $z$ 为正数，且 ${\begin{array}{l} x + y + x y = 8 \\ y + z + y z = 15 \\ z + x + z x = 35 \end{array}$ ，求 $x + y + z + x y$ 的值．

查看试题解析
19. 仔细阅读下面例题，解答问题：
例题：已知二次三项式 $x^{2} - 4 x + m$ 有一个因式是 $x + 3$ ，求另一个因式以及m的值．
解：设另一个因式为 $x + n$ ，则 $x^{2} - 4 x + m = (x + 3) (x + n)$ ，
即 $x^{2} - 4 x + m = x^{2} + (n + 3) x + 3 n$ ，
∴ ${\begin{array}{l} n + 3 = - 4 \\ 3 n = m \end{array}$ ，解得 ${\begin{array}{l} m = - 21 \\ n = - 7 \end{array}$ ．
故另一个因式为 $x - 7$ ， m的值为－21．
仿照上面的方法解答下面问题：
已知二次三项式 $x^{2} + 3 x - k$ 有一个因式是x-5，求另一个因式以及k的值．

查看试题解析
20. 阅读下列材料：
整体思想是数学解题中常用的一种思想方法：
下面是某同学对多项式 $(x^{2} - 3 x + 4) (x^{2} - 3 x + 6) + 1$ 进行因式分解的过程．
解：设 $x^{2} - 3 x = m$
原式 $= (m + 4) (m + 6) + 1$ （第一步）
      $= m^{2} + 10 m + 25$ （第二步）
      $= {(m + 5)}^{2}$ （第三步）
      $= {(x^{2} - 3 x + 5)}^{2}$ （第四步）
回答下列问题：

(1)、该同学第二步到第三步运用了因式分解的方法是．
      $A$ .提取公因式     $B$ .平方差公式     $C$ .完全平方公式

(2)、请你模仿以上方法尝试对多项式 $(a^{2} - 4 a + 2) (a^{2} - 4 a + 6) + 4$ 进行因式分解．

查看试题解析
21. 阅读材料，要将多项式 $a m + a n + b m + b n$ 分解因式，可以先把它的前两项分成一组，提出公因式a ，再把它的后两项分成一组，提出公因式b ，从而得到： $a m + a n + b m + b n = a (m + n) + b (m + n)$ ，这时 $a (m + n) + b (m + n)$ 中又有公因式 $(m + n)$ ，于是可以提出 $(m + n)$ ，从而得到 $(m + n) (a + b)$ ，因此有 $a m + a n + b m + b n = a (m + n) + b (m + n) = (m + n) (a + b)$ ，这种方法称为分组法．请回答下列问题：

(1)、尝试填空： $a c - b c + a b - a^{2} =$ ；

(2)、解决问题：因式分解 $2 x - 18 + x y - 9 y$ ；

(3)、拓展应用：已知三角形的三边长分别是a ， b ， c ，且满足 $a^{2} + 2 b^{2} + c^{2} - 2 a b - 2 b c = 0$ ，试判断这个三角形的形状，并说明理由．

查看试题解析
22. 数学课后，小玲和同桌小娟各自拿出自己的漂亮的正方形手帕，她们俩各有一条方格手帕和一条绣花手帕，如图，小玲说：“我的方格手帕的边长比你的方格手帕的边长大0.6 $c m$ ．”小娟说：“我的绣花手帕的边长比你的绣花手帕的边长大0.6 $c m$ ．”设小玲的两块手帕的面积和为 $S_{1}$ ，小娟的两块手帕的面积和为 $S_{2}$ ，请同学们运用因式分解的方法算一算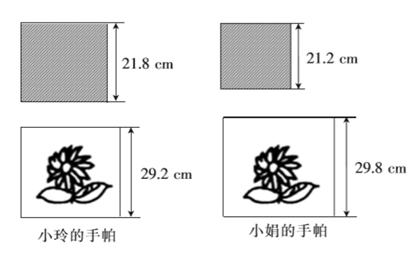 $S_{2}$ 与 $S_{1}$ 的差．

查看试题解析
23. 阅读以下材料：
因式分解： ${(x + y)}^{2} + 2 (x + y) + 1$ ，

解：令 $(x + y) = A$ ，则原式： $= A^{2} + 2 A + 1 = {(A + 1)}^{2}$ ，

再将“A”还原，得原式 $= {(x + y + 1)}^{2}$ ，

上述解题用到的是“整体思想”，“整体思想”是数学解题中常用的一种思想方法，请你解答下列问题：

(1)、因式分解： $1 - 2 (x - y) + {(x - y)}^{2}$ ；

(2)、当n为何值时，代数式 $(n^{2} - 2 n - 3) (n^{2} - 2 n + 5) + 17$ 有最小值？最小值为多少？

查看试题解析
24. 观察下面的等式： $3^{2} - 1^{2} = 8 \times 1$ ， $5^{2} - 3^{2} = 8 \times 2$ ， $7^{2} - 5^{2} = 8 \times 3$ ， $9^{2} - 7^{2} = 8 \times 4$ ， …．

(1)、尝试： $1 3^{2} - 1 1^{2} = 8 \times$ ．

(2)、归纳： ${(2 n + 1)}^{2} - {(2 n - 1)}^{2} = 8 \times$ （用含n的代数式表示，n为正整数）．

(3)、推理：运用所学知识，推理说明你归纳的结论是正确的．

查看试题解析
25. 阅读材料：
由多项式乘法得 $(x + a) (x + b) = x^{2} + (a + b) x + a b$ ，将该式从右到左使用，即可得到“十字相乘法”进行因式分解的公式： $x^{2} + (a + b) x + a b = (x + a) (x + b)$ ．
示例：
分解因式： $x^{2} + 5 x + 6 = x^{2} + (2 + 3) x + 2 \times 3 = (x + 2) (x + 3)$ ．

(1)、尝试：分解因式 $x^{2} + 6 x + 8 = (x +$ $) (x +$ $) ；$

(2)、应用：请用上述方法解方程 $x^{2} - 3 x - 4 = 0$ ．

(3)、拓展：用因式分解法解方程 $x^{2} - k x - 16 = 0$ 时，得到的两根均为整数，则 $k$ 的值可以为．

查看试题解析
26. 我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法，其实分解因式的方法还有分组分解法、添项拆项法、十字相乘法等等．①分组分解法：将一个多项式适当分组后，可提公因式或运用公式继续分解的方法叫作分组分解法．
例如： $4 x^{2} - 4 x - y^{2} + 1 = (4 x^{2} - 4 x + 1) - y^{2} = {(2 x - 1)}^{2} - y^{2} = (2 x - y - 1) (2 x + y - 1)$

②十字相乘法：十字相乘法能用于二次三项式的分解因式．

分解步骤：1．分解二次项，所得结果分别写在十字交叉线的左上角和左下角；2．分解常数项，所得结果分别写在十字交叉线的右上角和右下角；3．交叉相乘，求代数和，使其等于一次项；4．观察得出原二次三项式的两个因式，并表示出分解结果．这种分解方法叫作十字相乘法．

例如： $x^{2} - 3 x - 40$ 分析： $x^{2} - 3 x - 40$

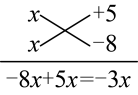
观察得出：两个因式分别为 $(x + 5)$ 与 $(x - 8)$

解：原式 $= (x + 5) (x - 8)$

③添项拆项法：将一个多项式的某一项拆成两项后，可提公因式或运用公式继续分解的方法叫作拆项法．

例如： $y^{2} - 10 y + 21 = y^{2} - 10 y + 25 - 4 = {(y - 5)}^{2} - 2^{2} = (y - 5 + 2) (y - 5 - 2) = (y - 3) (y - 7)$ ．

(1)、仿照以上方法，按照要求分解因式：
①（分组分解法） $a b - a - b + 1 =$ ；
②（十字相乘法） $y^{2} + 3 y - 10 =$ ；

(2)、已知：a、b、c为 $△ A B C$ 的三条边， $a^{2} + b^{2} + c^{2} - 6 a = 10 b + 8 c - 50$ ，判断 $△ A B C$ 的形状．

查看试题解析
27. 我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释，例如：图1可以用来解释 $a^{2} + 2 a b + b^{2} = (a + b)^{2}$ ．现有足够多的正方形卡片1号、2号，长方形卡片3号，如图3.

(1)、根据图2完成因式分解： $2 a^{2} + 2 a b =$ ；

(2)、现有1号卡片1张、2号卡片4张，3号卡片4张，在不重叠的情况下可以紧密地拼成一个大正方形，则这个大正方形的边长为；（用含 $a ､ b$ 的式子表示）

(3)、图1中的1号和2号卡片所占面积之和为 $S_{1}$ ，两个3号卡片所占面积之和为 $S_{2}$ ，求证： $S_{1} - S_{2} ⩾ 0$ ．

查看试题解析

【培优卷】2024年北师大版数学八（下）第四章因式分解 章末检测

一、选择题（每题2分，共20分）

二、填空题（每题3分，共15分）

三、计算题（共2题，共18分）

四、解答题（共10题，共67分）

【培优卷】2024年北师大版数学八（下）第四章因式分解章末检测