【培优卷】2024年北师大版数学八(下)4.3 公式法 同步练习
试卷更新日期:2024-03-24 类型:同步测试
一、选择题
-
1. 已知实数(x2﹣x)2﹣4(x2﹣x)﹣12=0,则代数式x2﹣x+1的值为( )A、﹣1 B、7 C、﹣1或7 D、以上全不正确2. n是整数,式子 [1﹣(﹣1)n](n2﹣1)计算的结果( )
A、是0 B、总是奇数 C、总是偶数 D、可能是奇数也可能是偶数3. 如果一个数等于两个连续奇数的平方差,那么我们称这个数为“幸福数”.下列数中,属于“幸福数”的是( )A、205 B、250 C、502 D、5204. 已知n(n≥8)个正实数 , , ···,满足= , 其中q是不为1的正数.则+ , 与+的大小关系为( )A、大于 B、等于 C、小于 D、不能确定5. 已知a,b,c为△ABC三边,且满足a2c2-b2c2=a4-b4 , 则它的形状为 ( )A、等边三角形 B、直角三角形 C、等腰三角形 D、等腰三角形或直角三角形6. 已知a,b,c分别是△ABC的三边长,若 , , 则△ABC的周长是( )A、3 B、6 C、8 D、127. 若将多项式因式分解为 , 则的值为( )A、 B、 C、 D、或8. 我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:F(n)= .例如:12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)= .如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数t为“吉祥数”.根据以上新定义,下列说法正确的有:(1)F(48)= ;(2)如果一个正整数m是另外一个正整数n的平方,我们称正整数m是完全平方数,则对任意一个完全平方数m,总有F(m)=1;(3)15和26是“吉祥数”;(4)“吉祥数”中,F(t)的最大值为 . ( )A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 在有理数范围内分解因式:(x+1)(x+2)(2x+3)(x+6)-20x4= .
10. 一个长方形的长与宽分别为 , , 若周长为 , 面积为 , 则的值为 .11. 已知 ,则代数式 的值为.12. 数348﹣1能被30以内的两位数(偶数)整除,这个数是 .13. 阅读材料回答问题:已知多项式有一个因式是 , 求的值.解法:设为整式
上式为恒等式,
当时, ,
即 .
解得: .
若多项式含有因式和 , 则 .
三、计算题
-
14. 把下列各式因式分解.(1)、;(2)、;(3)、;(4)、 .15. (y–z)2+(x–y)2+(z–x)2=(y+z–2x)2+(z+x–2y)2+(x+y–2z)2 . 求 的值.
四、实践探究题
-
16. 分解因式有一种很重要的方法叫“十字相乘法”,常用于二次三项式的分解因式,实质是逆用多项式的乘法过程:x2+( a+b)x+ab=(x+a)(x+b).这个方法的关键是把二次项系数和常数项分别都拆成两个因数的积,并使这两组因数交叉相乘再求和等于一次项系数.
例如:
 (1)、分解因式:
(1)、分解因式:①x2+2x-24=
②6x2-7x-3=
(2)、参考以上方法解方程:①x2 +2x-35=0;
②4x2-16x+15=0.
17. 教科书中这样写道:“形如的式子称为完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值、最小值等问题.例如:分解因式: .
解:原式;
再如:求代数式的最小值.
解:;
,
原式 ,
即当时,原式有最小值 .
学以致用:
(1)、用配方法分解因式:;其他方法不得分(2)、用配方法求多项式的最大值?并求出此时的值.18. 阅读下列材料:将一个形如的二次三项式因式分解时,如果能满足且 , 则可以把因式分解成 .例如:①;
② .
根据材料,把下列式子进行因式分解.
(1)、;(2)、;(3)、 .19. 19世纪的法国数学家苏菲·热门给出了一种分解因式的方法:他抓住了该式只有两项,而且属于平方和的形式,要使用公式就必须添一项 , 随即将此项减去,即可得.人们为了纪念苏菲·热门给出这一解法,就把它叫做“热门定理”。根据以上方法,把下列各式因式分解:
(1)、;(2)、.20. 数形结合是解决数学问题的重要思想方法,在学习“因式分解”时,我们可以借助直观、形象的几何模型来求解下面共有三种卡片:型卡片是边长为的正方形;型卡片是长为 , 宽为的长方形;型卡片是边长为的正方形.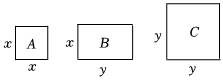 (1)、用张型卡片,张型卡片拼成如图的图形,根据图 , 多项式因式分解的结果为 ;
(1)、用张型卡片,张型卡片拼成如图的图形,根据图 , 多项式因式分解的结果为 ; (2)、请用张型卡片,张型卡片,张型卡片拼成一个大正方形,在图的虚线框中画出正方形的示意图,再据此写出一个多项式的因式分解.
(2)、请用张型卡片,张型卡片,张型卡片拼成一个大正方形,在图的虚线框中画出正方形的示意图,再据此写出一个多项式的因式分解. 21. 观察下列式子的因式分解做法:
21. 观察下列式子的因式分解做法:;
;
.
(1)、模仿以上做法,尝试对进行因式分解: .(2)、观察以上结果,猜想 为正整数,直接写结果,不用验证(3)、试求的值.22. 我们把多项式及叫做完全平方式.如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些非负数有关的问题或求代数式最大值、最小值等.例如:分解因式;例如求代数式的最小值.由可知,当时,有最小值,最小值是 .
根据阅读材料用配方法解决下列问题;
(1)、分解因式:;(2)、当a,b为何值时,多项式有最小值,并求出这个最小值;(3)、当a,b为何值时,多项式有最小值,并求出这个最小值.