河北省2024年中考数学模拟试卷(一)
试卷更新日期:2024-03-24 类型:中考模拟
一、选择题
-
1. 要使算式(-1)□3的运算结果最大,则“□”内应填入的运算符号为( )A、+ B、- C、× D、÷2. 有理数a,b在数轴上的对应点的位置如图所示,下列结论中不正确的是( )
 A、a-b<0 B、|a|<|b| C、a+b>0 D、ab>03. 如果长方形的长为(4a2-2a+1),宽为(2a+1),则这个长方形的面积为( )A、8a3-4a2+2a-1 B、8a3+4a2-2a-1 C、8a3-1 D、8a3+14. 一次数学活动中,小明对纸带沿AB折叠,量得 , 则的度数为( )
A、a-b<0 B、|a|<|b| C、a+b>0 D、ab>03. 如果长方形的长为(4a2-2a+1),宽为(2a+1),则这个长方形的面积为( )A、8a3-4a2+2a-1 B、8a3+4a2-2a-1 C、8a3-1 D、8a3+14. 一次数学活动中,小明对纸带沿AB折叠,量得 , 则的度数为( )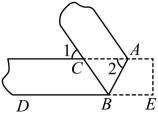 A、 B、 C、 D、5. 阳阳同学在复习老师已经批阅的作业本时,发现有一道填空题破了一个洞(如图),则破损部分的式子可能是( )
A、 B、 C、 D、5. 阳阳同学在复习老师已经批阅的作业本时,发现有一道填空题破了一个洞(如图),则破损部分的式子可能是( )化简:
A、 B、 C、 D、6. 如图,将直角三角形ABC沿AB方向平移2cm得到 , DF交BC于点H , , , 则阴影部分的面积为( )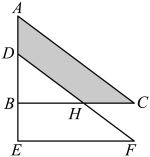 A、6cm2 B、8cm2 C、12cm2 D、16cm27. 某工厂用如图①所示的长方形和正方形纸板制作如图②所示的A、B两种长方体形状的无盖纸盒.现有正方形纸板120张,长方形纸板360张,刚好全部用完,则下列结论中正确的个数是 ( )
A、6cm2 B、8cm2 C、12cm2 D、16cm27. 某工厂用如图①所示的长方形和正方形纸板制作如图②所示的A、B两种长方体形状的无盖纸盒.现有正方形纸板120张,长方形纸板360张,刚好全部用完,则下列结论中正确的个数是 ( )①甲同学:设制作A型盒个数为x,根据题意可得4x+3×=360;②乙同学:设制作B型盒用正方形纸板的张数为m,根据题意可得3×+4(120-m)=360;③制作A型盒72个;④制作B型盒需正方形纸板共48张.
 A、1 B、2 C、3 D、48. 如图是测量一颗玻璃球体积的过程:(1)将300ml的水倒进一个容量为500ml的杯子中;(2)将四颗相同的玻璃球放入水中,结果水没有满;(3)再加一颗同样的玻璃球放入水中,结果水满溢出.
A、1 B、2 C、3 D、48. 如图是测量一颗玻璃球体积的过程:(1)将300ml的水倒进一个容量为500ml的杯子中;(2)将四颗相同的玻璃球放入水中,结果水没有满;(3)再加一颗同样的玻璃球放入水中,结果水满溢出.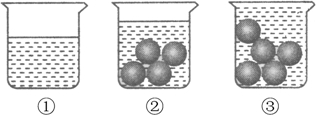
根据以上过程,推测这样一颗玻璃球的体积在( )
A、20cm3以上,30cm3以下 B、30cm3以上,40cm3以下 C、40cm3以上,50cm3以下 D、50cm3以上,60cm3以下9. 如图,在四边形中, , 以点为圆心,以任意长为半径作弧,分别交 , 于点 , , 分别以 , 为圆心,以大于长为半径作弧,两弧在内交于点 , 作射线 , 交于点 , 交的延长线于点若 , , 则的长为( )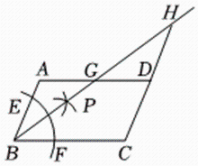 A、 B、 C、 D、10. 已知三角形的三边长分别为a,b,c,求其面积问题,中外数学家曾经进行过深入研究,古希腊的几何学家海伦(Heron,约公元50年)给出求其面积的海伦公式 , 其中;我国南宋时期数学家秦九韶(约1202—1261)曾提出利用三角形的三边求其面积的秦九韶公式 , 若一个三角形的三边长分别为2,3,4,则其面积是( )A、 B、 C、 D、11. 如图, 是 的八等分点. 若 , 四边形 的周长分别为 a, b,则下列判断正确的是( )
A、 B、 C、 D、10. 已知三角形的三边长分别为a,b,c,求其面积问题,中外数学家曾经进行过深入研究,古希腊的几何学家海伦(Heron,约公元50年)给出求其面积的海伦公式 , 其中;我国南宋时期数学家秦九韶(约1202—1261)曾提出利用三角形的三边求其面积的秦九韶公式 , 若一个三角形的三边长分别为2,3,4,则其面积是( )A、 B、 C、 D、11. 如图, 是 的八等分点. 若 , 四边形 的周长分别为 a, b,则下列判断正确的是( )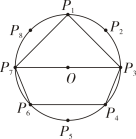 A、a<b B、a=b C、a>b D、a,b大小无法比较12. 已知△ABC中,AB=AC,求证:∠B<90°,下面写出运用反证法证明这个命题的四个步骤:
A、a<b B、a=b C、a>b D、a,b大小无法比较12. 已知△ABC中,AB=AC,求证:∠B<90°,下面写出运用反证法证明这个命题的四个步骤:①∴∠A+∠B+∠C> 180°,这与三角形内角和为180°矛盾.
②因此假设不成立,∠B<90°.
③假设在△ABC中,∠B≥90°.
④由AB=AC,得∠B=∠C≥90° ,即∠B+∠C≥180°.
这四个步骤正确的顺序应是( )
A、④③①② B、③④②① C、①②③④ D、③④①②13. 如图,D,E分别是△ABC的边AB,AC的中点.求证:DE∥BC,且.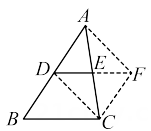
证明:延长 DE 至点 F,使 EF=DE,连结 FC,DC,AF.
又∵AE=EC,
∴四边形ADCF是平行四边形.
以下是接着的排序错误的证明步骤:
①∴DF∥BC.
②∴CF∥AD,即CF∥BD.
③∴四边形 DBCF 是平行四边形.
④∴DE∥BC,且正确的证明顺序应是( )
A、②→③→①→④ B、②→①→③→④ C、①→③→④→② D、①→③→②→④14. 如图,不等边内接于 , I是其内心, , , , 内切圆半径为( ) A、4 B、 C、 D、15. 学校组织学生参加知识问答,问答活动共设有20道选择题,各题分值相同,每题必答,如表记录了A、B、C三名学生的得分情况,按此规则,参赛学生D的得分可能是( ).
A、4 B、 C、 D、15. 学校组织学生参加知识问答,问答活动共设有20道选择题,各题分值相同,每题必答,如表记录了A、B、C三名学生的得分情况,按此规则,参赛学生D的得分可能是( ).参赛学生
答对题数
答错题数
得分
A
20
0
100
B
19
1
93
C
15
5
65
A、75 B、63 C、56 D、4416. 如图 , 动点从的顶点出发,沿匀速运动到点停止.在动点运动过程中,线段的长度与运动时间的函数关系如图所示,其中点为曲线部分的最低点,若的面积是 , 则图中的值为( )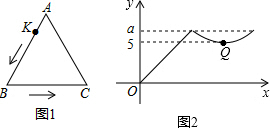 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
17. 已知a , b互为相反数,c , d互为倒数,m的绝对值是2,则= .18. 有一种手持烟花,该烟花有10个花弹,每1秒发一发花弹,每一发花弹的飞行路径均相同.第一发花弹的飞行高度(米)与飞行时间(秒)满足关系式:.当秒时,该花弹的高度为米.(1)、第一发花弹的飞行高度的最大高度是米.(2)、第一发花弹飞行过程中与其他花弹同一高度时,其的值为.19. 如图,在中, , , , 的顶点在轴的正半轴上,点 , 点在第一象限,且直角边平行于轴,反比例函数且的图象经过点和边的中点 , 则的值为 .

三、解答题
-
20. 聪聪根据市自来水公司的居民用水收费标准,制定了如下水费计算程序转换机示意图:
 (1)、根据该程序转换机计算表中a、b的值;(2)、当时,月应缴纳水费(元)用x的代数式表示为 ▲ ;
(1)、根据该程序转换机计算表中a、b的值;(2)、当时,月应缴纳水费(元)用x的代数式表示为 ▲ ;用户
张大爷
刘奶奶
王阿姨
聪聪家
用户
输入()
8
15
18
25
输入()
输出(元)
24
a
60
b
输出(元)
(3)、小丽家比小明家用水量多 , 水费多44元,则小丽家该月用水多少?21. 教育部办公厅印发了《关于加强中小学生手机管理的工作通知》,要求中小学生原则上不得将个人手机带入校园,确有需求的,须经家长同意、书面提出申请,进校后应将手机由学校统一保管,禁止带入课堂.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查,并绘制成如图(1),图(2)所示的统计图,已知“查资料”的人数是48人.

解答下列问题:
(1)、在扇形统计图中,表示“玩游戏”的扇形圆心角度数为 , 补全条形统计图;(2)、该校共有学生2 100人,估计每周使用手机时间在2 h以上(不含2 h)的人数;(3)、请写出一条学生健康使用手机的建议.22. 有4张背面完全相同的纸牌A,B,C,D,其中正面分别画有如图所示4个不同的几何图形,小华将这4张纸牌背面朝上洗匀后摸出1张,放回洗匀后再摸1张.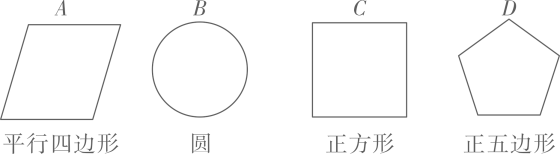 (1)、用画树状图或列表的方法表示两次摸牌所有可能出现的结果.(纸牌可用A,B,C,D表示)(2)、求摸出的两张纸牌正面所画的几何图形,既是轴对称图形又是中心对称图形的概率.23. 已知与成正比例,且时, .(1)、求与的函数关系式;(2)、将所得函数图象向上平移个单位,求平移后直线与坐标轴围成的三角形的面积.24.
(1)、用画树状图或列表的方法表示两次摸牌所有可能出现的结果.(纸牌可用A,B,C,D表示)(2)、求摸出的两张纸牌正面所画的几何图形,既是轴对称图形又是中心对称图形的概率.23. 已知与成正比例,且时, .(1)、求与的函数关系式;(2)、将所得函数图象向上平移个单位,求平移后直线与坐标轴围成的三角形的面积.24.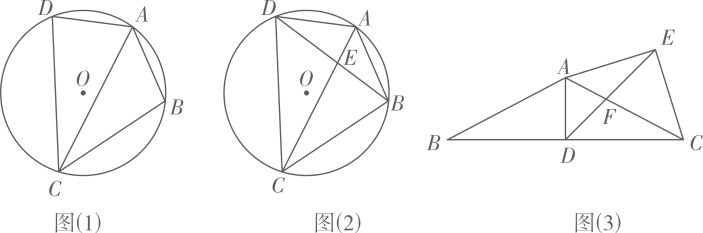 (1)、【感知】如图(1)已知四边形是圆O的内接四边形, , 易知 . (不用证明)(2)、【拓展】在【感知】的条件下,与交于点E,已知 , , 求的长.(3)、【应用】已知中 , 点D为中点,以为斜边向上作等腰直角三角形,当把的面积分为两部分时, .25. 科研人员为了研究弹射器的某项性能,利用无人机测量小钢球竖直向上运动的相关数据.无人机上升到离地面30米处开始保持匀速竖直上升,此时,在地面用弹射器(高度不计)竖直向上弹射一个小钢球(忽路空气阻力),在1秒时,它们距离地面都是35米,在6秒时,它们距离地面的高度也相同.其中无人机离地面高度(米)与小钢球运动时间(秒)之间的函数关系如图所示;小钢球离地面高度(米)与它的运动时间(秒)之间的函数关系如图中抛物线所示.
(1)、【感知】如图(1)已知四边形是圆O的内接四边形, , 易知 . (不用证明)(2)、【拓展】在【感知】的条件下,与交于点E,已知 , , 求的长.(3)、【应用】已知中 , 点D为中点,以为斜边向上作等腰直角三角形,当把的面积分为两部分时, .25. 科研人员为了研究弹射器的某项性能,利用无人机测量小钢球竖直向上运动的相关数据.无人机上升到离地面30米处开始保持匀速竖直上升,此时,在地面用弹射器(高度不计)竖直向上弹射一个小钢球(忽路空气阻力),在1秒时,它们距离地面都是35米,在6秒时,它们距离地面的高度也相同.其中无人机离地面高度(米)与小钢球运动时间(秒)之间的函数关系如图所示;小钢球离地面高度(米)与它的运动时间(秒)之间的函数关系如图中抛物线所示.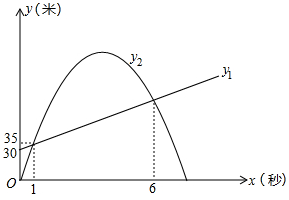 (1)、直接写出与之间的函数关系式;(2)、求出与之间的函数关系式;(3)、小钢球弹射1秒后直至落地时,小钢球和无人机的高度差最大是多少米?26. 在中, , , , 点是的中点四边形是菱形按逆时针顺序排列 , , 且 , 菱形可以绕点旋转,连接和 , 设直线和直线所夹的锐角为 .
(1)、直接写出与之间的函数关系式;(2)、求出与之间的函数关系式;(3)、小钢球弹射1秒后直至落地时,小钢球和无人机的高度差最大是多少米?26. 在中, , , , 点是的中点四边形是菱形按逆时针顺序排列 , , 且 , 菱形可以绕点旋转,连接和 , 设直线和直线所夹的锐角为 .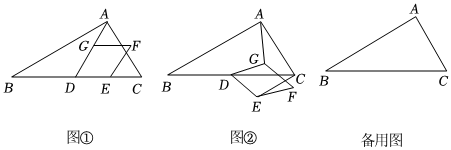 (1)、在菱形绕点旋转的过程中,当点在线段上时,如图 , 请直接写出与的数量关系及的值;(2)、当菱形绕点旋转到如图所示的位置时,中的结论是否成立?若成立,请写出证明过程;若不成立,请说明理由;(3)、设直线与直线的交点为 , 在菱形绕点旋转一周的过程中,当所在的直线经过点时,请直接写出的面积.
(1)、在菱形绕点旋转的过程中,当点在线段上时,如图 , 请直接写出与的数量关系及的值;(2)、当菱形绕点旋转到如图所示的位置时,中的结论是否成立?若成立,请写出证明过程;若不成立,请说明理由;(3)、设直线与直线的交点为 , 在菱形绕点旋转一周的过程中,当所在的直线经过点时,请直接写出的面积.