2024年重庆中考数学模拟试卷一(A卷)
试卷更新日期:2024-03-23 类型:中考模拟
一、选择题
-
1. 地球的海洋面积约为363000000平方米,其中数363000000用科学记数法表示为( )A、363×106 B、36.3×107 C、3.63×108 D、0.363×1092. 下列计算正确的是( )A、x4+x4=2x8 B、x3•x2=x6 C、(x﹣y)2=x2﹣y2 D、(x2y)3=x6y33. 下面几何体中,是圆锥的为( )A、
 B、
B、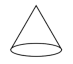 C、
C、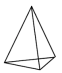 D、
D、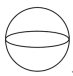 4. 若x=1是方程x2﹣mx+3=0的一个根,则m=( )A、3 B、4 C、﹣3 D、﹣45. 如图,直线AB∥CD , AD平分∠BDC , ∠1=70°,那么∠2的度数是( )
4. 若x=1是方程x2﹣mx+3=0的一个根,则m=( )A、3 B、4 C、﹣3 D、﹣45. 如图,直线AB∥CD , AD平分∠BDC , ∠1=70°,那么∠2的度数是( )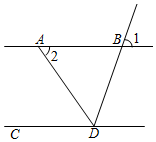 A、70° B、65° C、60° D、55°6. 如图,图①中有4个黑点,图②中有9个黑点,图③中有个黑点,…,按这样的规则排列下去,则图⑨中的黑点个数为( )
A、70° B、65° C、60° D、55°6. 如图,图①中有4个黑点,图②中有9个黑点,图③中有个黑点,…,按这样的规则排列下去,则图⑨中的黑点个数为( ) A、 B、 C、 D、7. 《九章算术》是中国传统数学最重要的著作之一,书中记载:“今有人共买兔,人出七,盈十一;人出五,不足十三,问人数几何?”意思是:“有若干人共同出钱买兔,如果每人出七钱,那么多了十一钱;如果每人出五钱,那么少了十三钱.问:共有几个人?”设有个人共同买兔,依题意可列方程为( )A、 B、 C、 D、8. 光线在不同介质中的传播速度不同,因此当光线从空气射向水中时,会发生折射.如图,在空气中平行的两条入射光线,在水中的两条折射光线也是平行的.若水面和杯底互相平行,且 , 则( )
A、 B、 C、 D、7. 《九章算术》是中国传统数学最重要的著作之一,书中记载:“今有人共买兔,人出七,盈十一;人出五,不足十三,问人数几何?”意思是:“有若干人共同出钱买兔,如果每人出七钱,那么多了十一钱;如果每人出五钱,那么少了十三钱.问:共有几个人?”设有个人共同买兔,依题意可列方程为( )A、 B、 C、 D、8. 光线在不同介质中的传播速度不同,因此当光线从空气射向水中时,会发生折射.如图,在空气中平行的两条入射光线,在水中的两条折射光线也是平行的.若水面和杯底互相平行,且 , 则( ) A、 B、 C、 D、9. 如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点处,折痕为EF,若∠ABE=30°,则的度数为( )
A、 B、 C、 D、9. 如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点处,折痕为EF,若∠ABE=30°,则的度数为( )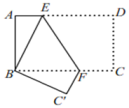 A、120° B、100° C、150° D、90°10. 如图,中, , 利用尺规在 , 上分别截取 , , 使;分别以 , 为圆心,以大于的长为半径作弧,两弧在内交于点;作射线交于点 , 过点作于点 , 则下列结论不一定正确的是( )
A、120° B、100° C、150° D、90°10. 如图,中, , 利用尺规在 , 上分别截取 , , 使;分别以 , 为圆心,以大于的长为半径作弧,两弧在内交于点;作射线交于点 , 过点作于点 , 则下列结论不一定正确的是( )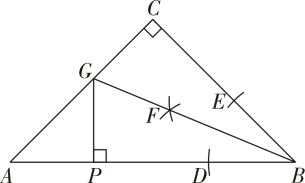 A、 B、
A、 B、
C、 D、二、填空题
-
11. 方程1﹣3x=0的解是 .12. 用一组、的值说明命题“若 , 则”是假命题,这组值可以是 , .13. 在一个不透明的口袋中,装有红色、黑色、白色的小球共40个,除颜色外其他完全相同,任意摸出一个球,记下颜色,放回后搅匀,重复上述过程,通过多次摸球试验后,摸到红色、黑色小球的频率分别稳定在0.25和0.45,则口袋中白球的个数可能是 .14. 如图,从笔直的公路旁一点出发,向西走3km到达 , 从出发向北走4km也到达.则从点向北偏西走到达.
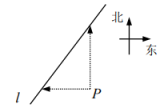 15. 一副三角板如图摆放,直线 , 则的度数是 .
15. 一副三角板如图摆放,直线 , 则的度数是 . 16. 如图,是菱形的一条对角线,以点为圆心,适当长为半径画弧,分别交 , 于点 , , 分别以点 , 为圆心,大于的长为半径画弧,两弧交于点;分别以点 , 为圆心,大于的长为半径画弧,两弧交于 , 两点,直线与射线交于点若 , 则
16. 如图,是菱形的一条对角线,以点为圆心,适当长为半径画弧,分别交 , 于点 , , 分别以点 , 为圆心,大于的长为半径画弧,两弧交于点;分别以点 , 为圆心,大于的长为半径画弧,两弧交于 , 两点,直线与射线交于点若 , 则 17. 若关于x的一元一次不等式组的解集为 , 且关于y的分式方程的解是整数,则符合条件的所有整数m的和为 .18. 一个四位数 , 若千位上的数字与百位上的数字之和与十位上的数字与个位上的数字之和的积等于 , 则称这个四位数为“六秩数”,例如,对于四位数 , , 为“六秩数”若 , , 记 , 则 ;若是一个“六秩数”,且是一个完全平方数,记 , 则的最大值与最小值的差为 .
17. 若关于x的一元一次不等式组的解集为 , 且关于y的分式方程的解是整数,则符合条件的所有整数m的和为 .18. 一个四位数 , 若千位上的数字与百位上的数字之和与十位上的数字与个位上的数字之和的积等于 , 则称这个四位数为“六秩数”,例如,对于四位数 , , 为“六秩数”若 , , 记 , 则 ;若是一个“六秩数”,且是一个完全平方数,记 , 则的最大值与最小值的差为 .三、解答题
-
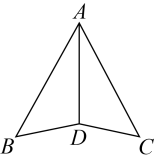
19.(1)、计算:-|-3|+2cos45°+(-1)2019-(2)、化简:20. 如图,已知平分 , . 求证: .
 21. 若与与的积与是同类项,求、的值.22. 某社区拟建A , B两类摊位以搞活“地摊经济”,每个A类摊位的占地面积比每个B类摊位的占地面积多2平方米,建A类摊位每平方米的费用为40元,建B类摊位每平方米的费用为30元,用60平方米建A类摊位的个数恰好是用同样面积建B类摊位个数的 .(1)、求每个A , B类摊位占地面积各为多少平方米?(2)、该社区拟建A , B两类摊位共90个,且B类摊位的数量不大于A类摊位数量的3倍,建造这90个摊位的总费用不超过10850元.则共有哪几种建造方案?(3)、在(2)的条件下,哪种方案的总费用最少?最少费用是多少?23. 如图,在直角坐标系中,△ABC三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).
21. 若与与的积与是同类项,求、的值.22. 某社区拟建A , B两类摊位以搞活“地摊经济”,每个A类摊位的占地面积比每个B类摊位的占地面积多2平方米,建A类摊位每平方米的费用为40元,建B类摊位每平方米的费用为30元,用60平方米建A类摊位的个数恰好是用同样面积建B类摊位个数的 .(1)、求每个A , B类摊位占地面积各为多少平方米?(2)、该社区拟建A , B两类摊位共90个,且B类摊位的数量不大于A类摊位数量的3倍,建造这90个摊位的总费用不超过10850元.则共有哪几种建造方案?(3)、在(2)的条件下,哪种方案的总费用最少?最少费用是多少?23. 如图,在直角坐标系中,△ABC三个顶点的坐标分别为A(0,3),B(3,4),C(2,2). (1)、将△ABC先向左平移4个单位长度,再向上平移1个单位长度,得到画出.(2)、画出将绕原点顺时针方向旋转后的.(3)、求的面积.24. 如图是一个正方体的展开图,已知它折叠成正方体后相对两个面上的数字之和相等.若从正方体展开图中这六个数中随机选出两个数分别作为一元二次方程中系数的值,请列表法或树状图法求这个一元二次方程没有实数根的概率.
(1)、将△ABC先向左平移4个单位长度,再向上平移1个单位长度,得到画出.(2)、画出将绕原点顺时针方向旋转后的.(3)、求的面积.24. 如图是一个正方体的展开图,已知它折叠成正方体后相对两个面上的数字之和相等.若从正方体展开图中这六个数中随机选出两个数分别作为一元二次方程中系数的值,请列表法或树状图法求这个一元二次方程没有实数根的概率. 25. 已知:在平面直角坐标系中,抛物线与x轴交于点 , , 与y轴交于点 .
25. 已知:在平面直角坐标系中,抛物线与x轴交于点 , , 与y轴交于点 . (1)、求抛物线的解析式;(2)、如图1,如果把抛物线x轴下方的部分沿x轴翻折 , 抛物线的其余部分保持不变,得到一个新图象.当平面内的直线与新图象有三个公共点时,求k的值;(3)、如图2,如果把直线沿y轴向上平移至经过点 , 与抛物线的交点分别是 , , 直线交于点 , 过点作于点 , 若 . 求点的坐标.26.
(1)、求抛物线的解析式;(2)、如图1,如果把抛物线x轴下方的部分沿x轴翻折 , 抛物线的其余部分保持不变,得到一个新图象.当平面内的直线与新图象有三个公共点时,求k的值;(3)、如图2,如果把直线沿y轴向上平移至经过点 , 与抛物线的交点分别是 , , 直线交于点 , 过点作于点 , 若 . 求点的坐标.26.如图,线段 是 的直径,弦 于点 ,点 是弧 上任意一点, .
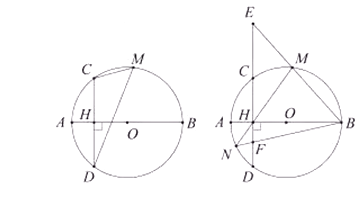 (1)、求 的半径 的长度;(2)、求 ;(3)、直线 交直线 于点 ,直线 交 于点 ,连接 交 于点 ,求 的值.
(1)、求 的半径 的长度;(2)、求 ;(3)、直线 交直线 于点 ,直线 交 于点 ,连接 交 于点 ,求 的值.