【培优卷】2024年浙教版数学七年级下册第3章整式的乘除单元测试

试卷更新日期：2024-03-22 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 已知2ⁿ＋2¹²＋1（n＜0）是一个有理数的平方，则n的值为（）

A、﹣16 B、﹣14 C、﹣12 D、﹣10

查看试题解析
2. 若 $x^{2} + a x + b = (x - 1) (x + 4)$ ，则 $a$ ， $b$ 的值分别是（）

A、 $a = 3$ ， $b = - 4$ B、 $a = - 3$ ， $b = 4$ C、 $a = - 3$ ， $b = - 4$ D、 $a = 3$ ， $b = 4$

查看试题解析
3. 若A＝(2＋1)(2²＋1)(2⁴＋1)(2⁸＋1)＋1，则A的末位数字是（）

A、2 B、4 C、6 D、8

查看试题解析
4. 如果 $m^{2} - 2 m - 3 = 0$ ，那么代数式 $(m + 3) (m - 3) + {(m - 2)}^{2}$ 的值为（）

A、0 B、 $- 1$ C、1 D、3

查看试题解析
5. 如果a＝（-2023）⁰ ， b＝（- $\frac{1}{10}$ ）， $c = {(- \frac{5}{3})}^{2}$ ，那么它们的大小关系为（）

A、a＞b＞c B、a＞c＞b C、c＞b＞a D、c＞a＞b

查看试题解析
6. 如图，正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为（2a+3b），宽为（a+2b）的大长方形，则需要A类、B类和C类卡片的张数分别为（）

A、 $2$ ， $8$ ， $5$ B、 $3$ ， $8$ ， $6$ C、 $3$ ， $7$ ， $5$ D、 $2$ ， $6$ ， $7$

查看试题解析
7. 如图，两个正方形的边长分别为a，b，如果a+b=7，ab=11，那么阴影部分的面积为（）

A、24 B、16 C、9 D、8

查看试题解析
8. 已知 $x^{2} + 4 y^{2} = 13$ ， $x y = 3$ ，求 $x + 2 y$ 的值，这个问题我们可以用边长分别为 $x$ 和 $y$ 的两种正方形组成一个图形来解决，其中 $x > y$ ，能较为简单地解决这个问题是图形是（）

A、 B、 C、 D、

查看试题解析
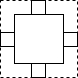9. 如图，在长方形ABCD中，AB=6，BC=10，其内部有边长为a的正方形AEFG与边长为b的正方形HIJK，两个正方形的重合部分也为正方形，且面积为5.若右侧阴影部分的面积S₂是左侧阴影部分面积S₁的4倍，则正方形AEFG与正方形HIJK的面积之和为（）

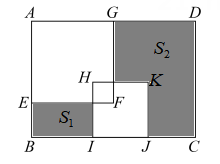A、20 B、25 C、 $\frac{49}{2}$ D、 $\frac{81}{4}$

查看试题解析
10. 下列计算中① $x (2 x^{2} - x + 1) = 2 x^{3} - x^{2} + 1$ ；② ${(a + b)}^{2} = a^{2} + b^{2}$ ；③ ${(x - 4)}^{2} = x^{2} - 4 x + 16$ ；④ $(5 a - 1) (- 5 a - 1) = 25 a^{2} - 1$ ；⑤ ${(- a - b)}^{2} = a^{2} + 2 a b + b^{2}$ ；正确的个数有…（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每题4分，共24分）

11. 计算： $2 (1 + \frac{1}{2}) (1 + \frac{1}{2^{2}}) (1 + \frac{1}{2^{4}}) (1 + \frac{1}{2^{8}}) + \frac{1}{2^{14}} =$ ．

查看试题解析
12. 要使 $(x + 3) (2 x^{2} + m x - 4)$ 的展开式中不含 $x^{2}$ 项，则m的值为．

查看试题解析
13. 已知 $4^{x} = 3$ ， $4^{y} = 8$ ，则 $4^{3 x - y}$ 的值为．

查看试题解析
14. 已知 $4 x^{2} - x = 1013$ ，则代数式 $(2 x + 1) (4 x - 3)$ 的值为.

查看试题解析
15. 如图，边长为6的正方形ABCD中放置两个长和宽分别为a，b的长方形，若长方形的周长为 16，面积为 15.75，则图中阴影部分的面积 $S_{1} + S_{2} + S_{3}$ =.

查看试题解析
16. 已知甲、乙两个长方形，它们的边长如图所示（ $m$ 为正整数），甲、乙的面积分别为 $S_{1}$ ， $S_{2}$ ．

(1)、 $S_{1}$ 与 $S_{2}$ 的大小关系为： $S_{1}$ $S_{2}$ （填“>”“=”或“<”）；

(2)、若满足 $| S_{2} - S_{1} | < n \leq 2023$ 的整数 $n$ 有且只有2个，则 $m$ 的值是．

查看试题解析

三、解答题（共8题，共66分）

17. 已知 $(a + b)^{a} \cdot (b + a)^{b} = (a + b)^{5}$ （a+b≠0或±1)，且 $(a - b)^{a + 4} \cdot (a - b)^{6 - b} = (a - b)^{7} (a - b \neq 0$ 或 $\pm 1)$ ，求 $a^{a} b^{b}$ 的值.

查看试题解析
18. 阅读材料并解答问题：我们已经知道，完全平方公式可以用平面几何图形的面积来表示，实际上还有一些代数恒等式也可以用这种形式表示，例如： $2 a (a + b) = 2 a^{2} + 2 a b$ 就可以用图①的面积来表示．

(1)、请写出图②所表示的代数恒等式．

(2)、请画图，用平面几何图形的面积来表示代数恒等式 $(a + b) (2 a + b) = 2 a^{2} + 3 a b + b^{2}$ ．

查看试题解析
19. 如图，某体育训练基地，有一块长 $(3 a - 5 b)$ 米，宽 $(a - b)$ 米的长方形空地，现准备在这块长方形空地上建一个长 $a$ 米，宽 $(a - 2 b)$ 米的长方形游泳池，剩余四周全部修建成休息区 $. ($ 结果需要化简 $)$

(1)、求长方形游泳池面积；

(2)、求休息区面积；

(3)、比较休息区与游泳池面积的大小关系．

查看试题解析
20. 如图是某住宅的平面结构示意图（单位：米），图中的四边形均是长方形或正方形．

(1)、用含x，y的代数式分别表示客厅和卧室（含卧室A，B）的面积；

(2)、若 $x - y = 2$ ， $x y = 8$ ，求卧室（含卧室A，B）比客厅大多少平方米．

查看试题解析
21.

(1)、计算观察下列各式填空：
第1个： $(a - b) (a + b) =$ ；
第2个： $(a - b) (a^{2} + a b + b^{2}) =$ ；
第3个： $(a - b) (a^{3} + a^{2} b + a b^{2} + b^{2}) =$ ；
这些等式反映出多项式乘法的某种运算规律．

(2)、猜想：若n为大于1的正整数，则 $(a - b) (a^{n - 1} + a^{n - 2} b + a^{n - 3} b^{2} + \cdot \cdot \cdot + a^{2} b^{n - 3} + a b^{n - 2} + b^{n - 1}) =$ ．

(3)、利用（2）的猜想结论计算： $2^{n - 1} + 2^{n - 2} + 2^{n - 3} + \cdot \cdot \cdot + 2^{3} + 2^{2} + 2 + 1 =$ ．

(4)、扩展与应用： $3^{n - 1} + 3^{n - 2} + 3^{n - 3} + \cdot \cdot \cdot + 3^{3} + 3^{2} + 3 + 1 =$ ．

查看试题解析
22. 如图①，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿线剪开，如图所示，拼成图②的长方形．

(1)、请你表示出图①中阴影部分的面积；
请你表示出图②中阴影部分的面；

(2)、比较两图的阴影部分面积，可以得到乘法公式：；

(3)、请应用公式计算： $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) ⋯ (1 - \frac{1}{202 2^{2}}) (1 - \frac{1}{202 3^{2}})$ ．

查看试题解析
23. 若x满足(9-x)(x-4)=4，求 ${(9 - x)}^{2} + (x - 4 ）^{2}$ 的值.
解：设9-x=a，x-4=b，则(9-x)(x-4)=ab=4，a+b=(9-x)+(x-4)=5，
$∴ (9 - x)^{2} + (x - 4)^{2} = a^{2} + b^{2} = (a + b)^{2} - 2 a b = 5^{2} - 2 \times 4 = 17 .$
请仿照上面的方法解答下面的问题：

(1)、若x满足(x-10)(x-20)=15，求 $(x - 10)^{2} + (x - 20)^{2}$ 的值.

(2)、若x满足( $(x - 2023)^{2} + (x - 2024)^{2} = 33 ，$ 求(x-2023)(x-2024)的值.

(3)、如图，已知正方形ABCD的边长为x，E，F分别是AD，DC上的点，且AE=1，CF=3，长方形EMFD的面积是48，分别以MF，DF为边长作正方形MFRN和正方形GFDH，求阴影部分的面积.

查看试题解析
24. 对于一个图形，通过不同的方法计算图形的面积，可以得到一个数学等式．例如由图1可以得到 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ ，这样就用图形面积验证了完全平方公式．

(1)、类似地，写出图2中所表示的数学等式为；

(2)、如图3，用不同的代数式表示大正方形的面积，由此得到的数学等式为；

(3)、利用上面（2）的结论解决问题：若 $x + y = 7 ， x y = 6$ ，求 ${(x - y)}^{2}$ 的值；

(4)、利用此方法也可以求出一些不规则图形的面积．如图4，将两个边长分别为a和b的正方形拼在一起，B、C、G三点在同一直线上，连接 $B D$ 和 $B F$ ，若这两个正方形的边长满足 $a + b = 16$ ， $a b = 63$ ，请求出阴影部分的面积．

查看试题解析

【培优卷】2024年浙教版数学七年级下册第3章整式的乘除 单元测试

一、选择题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、解答题（共8题，共66分）

【培优卷】2024年浙教版数学七年级下册第3章整式的乘除单元测试