湖北省襄阳市老河口市2023-2024学年八年级（上）期末数学试卷

试卷更新日期：2024-03-22 类型：期末考试

进入出卷网下载

一、选择题（本大题共10个小题，每小题3分，共30分。在每小题给出的四个选项中只有一项是符合题目要求的，请将其序号填涂在答题卡上相应位置。）

1. 下列运算正确的是（）

A、 $a^{3} \cdot a^{4} = a^{12}$ B、 ${(a^{3})}^{2} = a^{5}$ C、 ${(a^{2} b)}^{3} = a^{2} b^{3}$ D、 ${(- a^{2})}^{3} = - a^{6}$

查看试题解析
2. 下列变形是因式分解的是（）

A、 $x (x + 1) = x^{2} + x$ B、 $x^{2} + 2 x + 1 = (x + 1)^{2}$ C、 $x^{2} + x y - 3 = x (x + y) - 3$ D、 $x^{2} + 6 x + 4 = (x + 3)^{2} - 5$

查看试题解析
3. 在 $\frac{1}{3} ， \frac{2}{x} ， \frac{x + 1}{2} ， \frac{x - y}{x + y}$ 中，分式的个数是（）

A、4 B、3 C、2 D、1

查看试题解析
4. 分式 $\frac{1}{x + 1}$ 有意义的条件是（）

A、 $x \neq 1$ B、 $x \neq - 1$ C、 $x \neq 0$ D、 $x = - 1$

查看试题解析
5. 分式方程 $\frac{2}{x - 3} = \frac{1}{x}$ 的解是（）

A、 $x = - 3$ B、 $x = 3$ C、 $x = - 1$ D、 $x = 1$

查看试题解析
6. 三角形的面积是 $12 a^{3} - 6 a b + 3 a^{2}$ ，它的一条高是3a，这条高对应的底边长是（）

A、 $8 a^{2} - 4 b + 2 a$ B、 $a^{2} + 2 b - 4 a$ C、 $a^{2} - 2 b + 4 a$ D、 $4 a^{2} - 2 b + a$

查看试题解析
7. 如果 $a + b = 4 ， a b = 2$ ，那么 $a^{2} + b^{2}$ 的值为（）

A、20 B、14 C、12 D、10

查看试题解析
8. 直角三角形中两个锐角的平分线相交所成的钝角的度数为（）

A、 $9 0^{°}$ B、 $13 5^{°}$ C、 $12 0^{°}$ D、 $4 5^{°}$ 或 $13 5^{°}$

查看试题解析
9. 如图， $B E = C D ， A E = A D ， ∠ 1 = ∠ 2 = 10 0^{°} ， ∠ B A E = 6 0^{°}$ ，则 $∠ C A E$ 的度数为（）

A、 $2 0^{°}$ B、 $3 0^{°}$ C、 $4 0^{°}$ D、 $5 0^{°}$

查看试题解析
10. 如图， $△ A B C$ 是边长为 20 的等边三角形，点 $D$ 是BC边上任意一点， $D E ⊥ A B$ 于点 $E ， D F ⊥ A C$ 于点 $F$ ，则 $B E + C F =$ （）

A、5 B、20 C、15 D、10

查看试题解析

二、填空题：（本大题共6个小题，每小题3分，共18分。把答案填在答题卡的对应位置的横线上。）

11. 计算： $2^{- 2} =$ ．

查看试题解析
12. 因式分解： $8 a^{3} b^{2} + 12 a b^{3} c$ = ．

查看试题解析
13. 如图，长方形花园ABCD中，AB=a，AD=b，花园中建有一条长方形的小路和一条平行四边形小路（阴影部分），两条小路的出口宽均为c．对花园中小路以外的部分进行绿化，则绿化部分的面积为．

查看试题解析
14. 如图，在 $△ A B C$ 中， $A B = A C ， A B = 5 ， B C = 3$ ，分别以 $A ， B$ 两点为圆心，大于 $\frac{1}{2} A B$ 的长为半径画圆弧，两弧相交于点M，N，连接MN与AC相交于点D，则 $△ B D C$ 的周长为．

查看试题解析
15. 若关于x的方程 $\frac{1}{x} + \frac{1}{x + 2} = \frac{2 m}{x (x + 2)}$ 无解，则m的值为．

查看试题解析
16. 如图，在 $△ A B C$ 中， $∠ B A C = 3 0^{°} ， A D$ 平分 $∠ B A C$ ，点 $E$ 在 $B C$ 的延长线上， $∠ C A E = 7 5^{°}$ ，若 $C E = B A + A C$ ，则 $∠ B$ 的度数为．

查看试题解析

三、解答题（本大题共9个小题，共72分。解答应写出文字说明，证明过程或演算步骤，并且写在答题卡上每题对应的答题区域内。）

17. 计算：

(1)、 $(x + y) (x^{2} - x y + y^{2})$ ；

(2)、 $(12 a^{3} - 6 a^{2} + 3 a) \div 3 a$ ；

(3)、 $(\frac{2}{x - 3} - \frac{1}{x}) \cdot \frac{x^{2} - 3 x}{x^{2} + 6 x + 9}$ ．

查看试题解析
18. 如图， $C A = C D$ ， $∠ 1 = ∠ 2$ ， $B C = E C$ ．求证： $A B = D E$ ．

查看试题解析
19. 先化简，再求值： $(2 a + b)^{2} + (a + b) (a - b)$ ，其中 $a = 1 ， b = - 2$

查看试题解析
20. 化简： $(1 + \frac{a}{2 - a}) \div \frac{4 - a^{2}}{a^{2} - 4 a + 4}$ 并在-2，0，2中选择一个合适的a值代入求值．

查看试题解析
21. 由小正方形组成的3×3的网格中，每个小正方形的顶点称为格点．A，B，C均为格点．在给定的网格中，按下列要求画图（每小题只画一种即可）：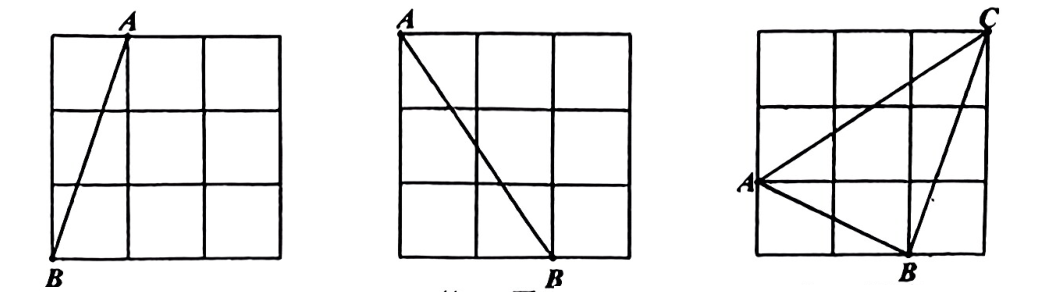
图① 图② 图③

(1)、
在图①中，画一条不与AB重合的线段MN，使MN与AB关于某条直线对称，且M，N为格点．

(2)、在图②中，画一条不与AB重合的线段PQ，使PQ与AB关于某条直线对称，且P，Q为格点．

(3)、在图③中，画一个△DEF，使△DEF与△ABC关于某条直线对称，且D，E，F为格点．

查看试题解析
22. 先化简，再求值： $(\frac{x + 2}{x^{2} - 2 x} - \frac{x - 1}{x^{2} - 4 x + 4}) \div \frac{x - 4}{x}$ 其中 $x$ 满足 $(x - 1) (x - 3) = 1$

查看试题解析
23. 某汽车有油和电两种驱动方式，两种驱动方式不能同时使用，该汽车从A地行驶至B地，全程用油驱动需96元油费，全程用电驱动需16元电费，已知每行驶1千米，用油比用电的费用多0.8元．

(1)、求该汽车用电驱动方式行驶1千米的电费：

(2)、从A地行驶至B地，若用油和用电的总费用不超过40元，则至少需用电行驶多少千米？

查看试题解析
24. 如图，在 $△ A B C$ 中， $A B = A C$ ，点 $D$ 为 $B C$ 边的中点， $D E ⊥ A B$

(1)、求证：∠CAD＝∠BDE；

(2)、作DF∥AB，交AC于点F，若AB=6，求DF的长．

查看试题解析
25. 问题提出：在 $△ A B C$ 中， $∠ A C B = 9 0^{°} ， A C = B C$ ，直线MN经过点 $C$ ，且 $A D ⊥ M N$ 于点 $D ， B E ⊥ M N$ 于点 $E$ . 探究线段 $D E ， A D ， B E$ 之间的数量关系.

(1)、分类探究：
如图1，当A，B两点在直线MN同侧时．①求证： $△ A D C ≅ △ C E B$ ；
②推断：线段DE，AD，BE之间的数量关系是；

(2)、如图2，当A，B两点在直线MN异侧时，请探究线段DE，AD，BE之间的数量关系，并写出证明过程；

(3)、拓展运用：
如图3， $∠ A C B = 9 0^{°} ， A C = B C ， A (- 3 ， m) ， B (2 ， n) ， C (- 1 ， - 1)$ ，请直接写出m，n的值．

查看试题解析