浙江省杭州市保俶塔教育集团2023学年八年级上学期数学期中质量检测试卷
试卷更新日期:2024-03-22 类型:期中考试
一、仔细选一选(本题有10个小题,每小题3分,共30分)
-
1. 下列常见的微信表情包中,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如果三角形两边长分别是6厘米、8厘米,那么第三边长可能是( )A、16厘米 B、14厘米 C、10厘米 D、2厘米3. 一元一次不等式x+1>2的解在数轴上表示为( )A、
2. 如果三角形两边长分别是6厘米、8厘米,那么第三边长可能是( )A、16厘米 B、14厘米 C、10厘米 D、2厘米3. 一元一次不等式x+1>2的解在数轴上表示为( )A、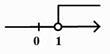 B、
B、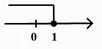 C、
C、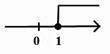 D、
D、 4. 下列语句中,是真命题的是( )A、已知a2=4,求a的值 B、面积相等的两个三角形全等 C、对顶角相等 D、若ab , 则a2>b25. 如图,CD⊥AB于点D , EF⊥AB于点F , CD=EF . 要根据“HL”证明Rt△ACD≌Rt△BEF , 则还需要添加的条件( )
4. 下列语句中,是真命题的是( )A、已知a2=4,求a的值 B、面积相等的两个三角形全等 C、对顶角相等 D、若ab , 则a2>b25. 如图,CD⊥AB于点D , EF⊥AB于点F , CD=EF . 要根据“HL”证明Rt△ACD≌Rt△BEF , 则还需要添加的条件( )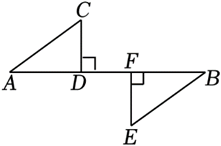 A、∠A=∠B B、AC=BE C、AD=BE D、AD=BF6. 已知如图中的两个三角形全等,则的度数是( )
A、∠A=∠B B、AC=BE C、AD=BE D、AD=BF6. 已知如图中的两个三角形全等,则的度数是( )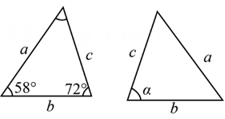 A、 B、 C、 D、7. 若实数m、n满足等式|m﹣2|+=0,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是( )A、6 B、6或8 C、8或10 D、108. 把一些书分给同学,设每个同学分x本.若 ▲ ;若分给11个同学,则书有剩余.可列不等式8(x+6)>11x , 则横线的信息可以是( )A、分给8个同学,则剩余6本 B、分给6个同学,则剩余8本 C、分给8个同学,则每人可多分6本 D、分给6个同学,则每人可多分8本9. 如图,过边长为3的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,且CQ=PA,连接PQ交AC于点D,则DE的长为( )
A、 B、 C、 D、7. 若实数m、n满足等式|m﹣2|+=0,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是( )A、6 B、6或8 C、8或10 D、108. 把一些书分给同学,设每个同学分x本.若 ▲ ;若分给11个同学,则书有剩余.可列不等式8(x+6)>11x , 则横线的信息可以是( )A、分给8个同学,则剩余6本 B、分给6个同学,则剩余8本 C、分给8个同学,则每人可多分6本 D、分给6个同学,则每人可多分8本9. 如图,过边长为3的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,且CQ=PA,连接PQ交AC于点D,则DE的长为( ) A、1 B、 C、2 D、10. 如图,在四边形ABCD中,AC平分∠BAD , CE⊥AB于点E , ∠ADC+∠ABC=180°,有下列结论:①CD=CB;②AD+AB=2AE;③∠ACD=∠BCE;④-=2 , 其中正确的是( )
A、1 B、 C、2 D、10. 如图,在四边形ABCD中,AC平分∠BAD , CE⊥AB于点E , ∠ADC+∠ABC=180°,有下列结论:①CD=CB;②AD+AB=2AE;③∠ACD=∠BCE;④-=2 , 其中正确的是( ) A、② B、①②③ C、①②④ D、①②③④
A、② B、①②③ C、①②④ D、①②③④二、认真填一填(本题有6个小题,每小题4分,共24分)
-
11. “x与7的和大于2”用不等式表示为 .12. 写出“等腰三角形两底角相等”的逆命题:.13. 如图,在△ABC中,∠B=65°,∠C=30°,分别以点A和点C为圆心,大于AC长为半径画弧,两弧相交于点M , N , 作直线MN , 连接AD , 则∠BAD的度数为 .
 14. 如图,已知是等腰直角三角形, , , 将沿直线平移到的位置,当恰好是中点时,则AE=.
14. 如图,已知是等腰直角三角形, , , 将沿直线平移到的位置,当恰好是中点时,则AE=. 15. 已知关于x、y的二元一次方程组(k为常数).(1)、若该方程组的解x , y满足x+y<3,则k的取值范围为;(2)、若该方程组的解x , y均为正整数,且k<3,则该方程组的解为 .16. 如图,折叠等腰三角形纸片ABC , 使点C落在边AB上的点F处,折痕为DE , 已知AB=AC , FD⊥BC .
15. 已知关于x、y的二元一次方程组(k为常数).(1)、若该方程组的解x , y满足x+y<3,则k的取值范围为;(2)、若该方程组的解x , y均为正整数,且k<3,则该方程组的解为 .16. 如图,折叠等腰三角形纸片ABC , 使点C落在边AB上的点F处,折痕为DE , 已知AB=AC , FD⊥BC . (1)、则∠AFE=度;(2)、如果AF=4,BF=6,则AE= .
(1)、则∠AFE=度;(2)、如果AF=4,BF=6,则AE= .三、全面答一答(本题有8个小题,共66分)
-
17. 解不等式组:(1)、;(2)、.18. 已知:如图,AD,BC相交于点O,OA=OD,AB∥CD.
求证:AB=CD.
 19. 在如图所示的网格中,每个小正方形的边长均为1个单位.
19. 在如图所示的网格中,每个小正方形的边长均为1个单位. (1)、请你在图1中画一个以格点为顶点,面积为3个平方单位的等腰三角形.(画一个即可)(2)、请你在图2中画一条以格点为端点,长度为的线段.(画一条即可)(3)、请你在图3中画一个以格点为顶点,为直角边的直角三角形.(画一个即可)20. 如图,已知在△ABC中,高线AD , BE相交于点H , 点F是BH的中点,∠ABC=45°.
(1)、请你在图1中画一个以格点为顶点,面积为3个平方单位的等腰三角形.(画一个即可)(2)、请你在图2中画一条以格点为端点,长度为的线段.(画一条即可)(3)、请你在图3中画一个以格点为顶点,为直角边的直角三角形.(画一个即可)20. 如图,已知在△ABC中,高线AD , BE相交于点H , 点F是BH的中点,∠ABC=45°. (1)、求证:△BHD≌△ADC.(2)、若DF=5,则求AC的长度.21. 如图,在△ABC中,AB=AC , D,E分别是AB,BC的中点,连结AE , 在AE上取点F , 使得EF=AD , 延长DF交AC于点G.
(1)、求证:△BHD≌△ADC.(2)、若DF=5,则求AC的长度.21. 如图,在△ABC中,AB=AC , D,E分别是AB,BC的中点,连结AE , 在AE上取点F , 使得EF=AD , 延长DF交AC于点G. (1)、当∠BAC=60°时,求∠AGD的度数.(2)、设∠BAC=α , ∠AGD=β , 探究α , β之间的关系.22. 为了测量一条两岸平行的河流的宽度,由于跨河测量困难,所以三个数学研究小组设计了不同的方案,他们在河南岸的点B处测得河北岸的树A恰好在B的正北方向,测量方案如下表:
(1)、当∠BAC=60°时,求∠AGD的度数.(2)、设∠BAC=α , ∠AGD=β , 探究α , β之间的关系.22. 为了测量一条两岸平行的河流的宽度,由于跨河测量困难,所以三个数学研究小组设计了不同的方案,他们在河南岸的点B处测得河北岸的树A恰好在B的正北方向,测量方案如下表:课题
测量河流宽度
工具
测量角度的仪器,标杆,皮尺等
小组
第一小组
第二小组
第三小组
测量方案
观察者从B点向东走到C点,此时恰好测得:
∠ACB=45°
观测者从B点向东走到O点,在O点插上一面标杆,继续向东走相同的路程到达C点后,一直向南走到点D , 使得树,标杆,人在同一直线上
观测者从B点出发,沿着南偏西80°的方向走到点C , 此时恰好测得:
∠ACB=40°
测量示
意
图


 (1)、第一小组认为要知道河宽AB , 只需要测量线段_的长度.(2)、第二小组认为只要测得CD就能得到河宽AB , 你认为第二小组的方案可行吗?如果可行,请给出证明;如果不可行,请说明理由.(3)、第三小组测得BC=35米,请你帮他们求出河宽AB .23. 如图,已知在△ABC中,∠B=90°,AC=10,BC=6,若动点P从点B开始,按B→A→C→B的路径运动,且速度为每秒2个单位长度,设出发的时间为t秒.
(1)、第一小组认为要知道河宽AB , 只需要测量线段_的长度.(2)、第二小组认为只要测得CD就能得到河宽AB , 你认为第二小组的方案可行吗?如果可行,请给出证明;如果不可行,请说明理由.(3)、第三小组测得BC=35米,请你帮他们求出河宽AB .23. 如图,已知在△ABC中,∠B=90°,AC=10,BC=6,若动点P从点B开始,按B→A→C→B的路径运动,且速度为每秒2个单位长度,设出发的时间为t秒. (1)、出发2秒后,求CP的长;(2)、出发几秒钟后,△BCP的面积等于18?(3)、当t为何值时,△BCP为等腰三角形?(直接写出答案)24. 如图,在等腰△ABC中,∠CAB=∠CBA , 作射线BC , AD是腰BC的高线,E是△ABC外射线BC上一动点,连结AE .
(1)、出发2秒后,求CP的长;(2)、出发几秒钟后,△BCP的面积等于18?(3)、当t为何值时,△BCP为等腰三角形?(直接写出答案)24. 如图,在等腰△ABC中,∠CAB=∠CBA , 作射线BC , AD是腰BC的高线,E是△ABC外射线BC上一动点,连结AE . (1)、当AD=4,BC=5时,求CD的长.(2)、当BC=CE时,求证:AE⊥AB .(3)、设△ACD的面积为S1 , △ACE的面积为S2 , 且 , 在点E的运动过程中,是否存在△ACE为等腰三角形,若存在,求出相应的的值,若不存在,请说明理由.
(1)、当AD=4,BC=5时,求CD的长.(2)、当BC=CE时,求证:AE⊥AB .(3)、设△ACD的面积为S1 , △ACE的面积为S2 , 且 , 在点E的运动过程中,是否存在△ACE为等腰三角形,若存在,求出相应的的值,若不存在,请说明理由.