浙江省宁波市海曙区2023-2024学年八年级上学期期末数学试题

试卷更新日期：2024-03-22 类型：期末考试

进入出卷网下载

一、选择题（本题共10小题，每小题3分，共30分．每小题只有一个选项是正确的）

1. 第19届杭州亚运会上，中国运动员全力以赴地参赛，最终取得骄人战绩。下列运动标识中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若 $a > b$ ，则下列式子中正确的是（）

A、 $\frac{a}{2} < \frac{b}{2}$ B、 $a - 3 < b - 3$ C、 $- 3 a < - 3 b$ D、 $a - b < 0$

查看试题解析
3. 对于命题“若 $a > b$ ，则 $| a | > | b |$ ”，能说明它是假命题的反例是（）

A、 $a = 3$ ， $b = 2$ B、 $a = 3$ ， $b = 4$ C、 $a = - 3$ ， $b = - 2$ D、 $a = 2$ ， $b = - 2$

查看试题解析
4. 下列计算：（1） ${(\sqrt{2})}^{2} = 2$ ，（2） $\sqrt{12} - \sqrt{3} = \sqrt{3}$ ，（3） $\sqrt{45} \div \sqrt{5} = 3$ ，（4） $(\sqrt{2} + \sqrt{3}) (\sqrt{2} - \sqrt{3}) = - 1$ ，其中结果正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
5. 已知 $A (2, a)$ ， $B (b, - 3)$ 是平面直角坐标系上的两个点， $A B ∥ x$ 轴，且点B在点A的右侧．若 $A B = 5$ ，则（）

A、 $a = - 3$ ， $b = - 3$ B、 $a = - 3$ ， $b = 7$ C、 $a = 2$ ， $b = 2$ D、 $a = - 8$ ， $b = 2$

查看试题解析
6. 将一副三角板按如图所示的方式放置，图中∠CAF的大小等于（）

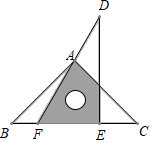A、50° B、60° C、75° D、85°

查看试题解析
7. 关于x的一元二次方程 $a x^{2} - 4 x - 1 = 0$ 有实数根，则a满足（）

A、 $a \geq 4$ 且 $a \neq 0$ B、 $a \geq - 4$ 且 $a \neq 0$ C、 $a \geq - 4$ D、 $a > - 4$

查看试题解析
8. 如图，在△ABC中，∠C＝90°，以A为圆心，任意长为半径画弧，分别交AC，AB于点M，N，再分别以M，N为圆心，大于 $\frac{1}{2}$ MN长为半径画弧，两弧交点O，作射线AO，交BC于点E.已知CE＝3，BE＝5，则AC的长为（　　）

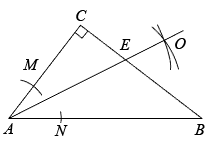A、8 B、7 C、6 D、5

查看试题解析
9. 如图，甲、乙两人分别骑自行车和摩托车，从同一地点沿相同的路线前往距离 $120 k m$ 的某地．如图 $l_{1}$ ， $l_{2}$ 分别表示甲、乙两人离开出发地的距离 $s (k m)$ 与行驶时间 $t (h)$ 之间的函数关系.问乙出发（）后两人相遇.

A、 $\frac{7}{3}$ 小时 B、 $\frac{5}{3}$ 小时 C、 $\frac{2}{3}$ 小时 D、1.5小时

查看试题解析
10. 如图，将一张直角梯形纸板（ $C D ∥ A B$ ， $A B ⊥ A D$ ）剪成3部分，恰好能拼成一个等腰三角形，若想知道1号部分的周长，则只需测量下列哪条线段即可（）

A、 $A E$ B、 $A D$ C、 $B E$ D、 $B C$

查看试题解析

二、填空题（本题有6个小题，每小题3分，共18分）

11. 若二次根式 $\sqrt{x - 1}$ 有意义，则x的取值范围是

查看试题解析
12. 已知，在 $△ A B C$ 中， $∠ A = ∠ B + ∠ C$ ，则 $△ A B C$ 是三角形.

查看试题解析
13. 有一边长为3的等腰三角形，它的两边长是方程x²-4x+k=0的两根，则k = ．

查看试题解析
14. 小明用200元钱去购买笔记本和钢笔共30件，已知每本笔记本4元，每支钢笔10元，则小明至少能买笔记本本.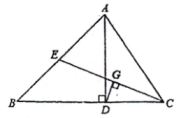

查看试题解析
15. 如图，在 $△ A B C$ 中， $A D$ 是 $B C$ 边上的高线， $C E$ 是 $A B$ 边上的中线， $D G ⊥ C E$ 于点G， $C D = A E$ ，若 $B D = 8$ ， $C D = 5$ ，则 $△ D C G$ 的面积是.

查看试题解析
16. 已知，一次函数 $y = - \frac{3}{4} x + 6$ 的图象与x轴、y轴分别交于点A、点B，在第一象限内有一点P，使得 $△ A B P$ 是等腰直角三角形，则点P的横坐标为.

查看试题解析

三、解答题（本题有7小题，共52分）

17. 解下列方程：

(1)、解方程： $x^{2} + 2 x = 0$ ；

(2)、解方程： ${(x - 3)}^{2} = 2 (x - 3)$ .

查看试题解析
18. 已知x满足 ${\begin{cases} 3 (x - 1) + 1 > - 5 \\ - x + 2 > 0 \end{cases}$ ，

(1)、求x的取值范围；

(2)、化简： $\sqrt{{(x - 2)}^{2}} + \sqrt{x^{2} + 2 x + 1}$ .

查看试题解析
19. $△ A B C$ 在平面直角坐标系中的位置如图所示，A、B、C三点在格点上.

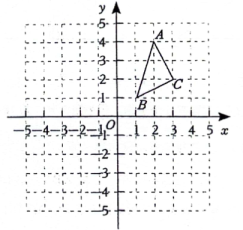(1)、作出 $△ A B C$ 关于y轴对称后的图形 $△ A_{1} B_{1} C_{1}$ ；

(2)、判断 $△ A B C$ 的形状，并说明理由.

查看试题解析
20. 如图，△ABC中，AB=AC，点E，D，F分别在三边上，且BE=CD，CF=BD．

(1)、求证：△BDE≌△CFD；

(2)、若∠EDF=50°，求∠A的度数．

查看试题解析
21. 已知一次函数 $y_{1} = k x + b$ （k、b是常数， $k \neq 0$ ）的图象过 $A (- 1 ， 3)$ ， $B (2 ， 0)$ .

(1)、求 $y_{1}$ 函数的表达式.

(2)、若函数 $y_{2} = m x + n$ （m，n是常数， $m > 0$ ）的图象过 $B (2 ， 0)$ ，当 $y_{1} < y_{2}$ 时，x的取值范围为.

查看试题解析
22. 端午节期间，某食品店平均每天可卖出300只粽子，卖出1只粽子的利润是1元．经调查发现，零售单价每降0.1元，每天可多卖出100只粽子．为了使每天获取的利润更多，该店决定把零售单价下降m（0＜m＜1）元．

(1)、零售单价下降0.2元后，该店平均每天可卖出只粽子，利润为元．

(2)、在不考虑其他因素的条件下，当m定为多少时，才能使该店每天获取的利润是420元并且卖出的粽子更多？

查看试题解析
23. 已知 $△ A B C$ 和 $△ D E C$ 都是等腰直角三角形，且 $∠ A C B = ∠ D C E = 90 °$ .

(1)、如图1，点D在 $△ A B C$ 内，求证： $A D ⊥ B E$ ；

(2)、如图2，A、D、E三点在同一条直线上，若 $A B = 13 \sqrt{2}$ ， $D E = 10$ ，求 $△ A C D$ 的面积；

(3)、如图3，若 $A B = 19$ ，点D在边 $A B$ 上运动，求 $△ B D E$ 周长的最小值.

查看试题解析