浙江省宁波市南三县2023-2024学年八年级上学期期末数学试题
试卷更新日期:2024-03-22 类型:期末考试
一、单选题
-
1. 第19届亚运会将于2022年9月在杭州举行,下列历届亚运会会徽是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在平面直角坐标系中,点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 线段 , , 首尾顺次相接组成三角形,若 , , 则的长度可以是( )A、4 B、5 C、6 D、74. 若成立,则下列不等式成立的是( )A、 B、 C、 D、5. 能说明命题“对于任何实数 , ”是假命题的一个反例可以是( )A、 B、 C、 D、6. 如图,在同一条直线上, , 添加下列哪一个条件可以使( )
2. 在平面直角坐标系中,点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 线段 , , 首尾顺次相接组成三角形,若 , , 则的长度可以是( )A、4 B、5 C、6 D、74. 若成立,则下列不等式成立的是( )A、 B、 C、 D、5. 能说明命题“对于任何实数 , ”是假命题的一个反例可以是( )A、 B、 C、 D、6. 如图,在同一条直线上, , 添加下列哪一个条件可以使( ) A、 B、 C、 D、7. 若点位于第二象限,则的取值范围是( )A、 B、 C、 D、8. 若一次函数的图象经过点和点 , 当时, , 则的取值范围是( )A、 B、 C、 D、9. 如图,在中,于点 . 分别以为边向外作正方形,得到较大的三个正方形的面积分别为 , 那么最小的正方形面积为( )
A、 B、 C、 D、7. 若点位于第二象限,则的取值范围是( )A、 B、 C、 D、8. 若一次函数的图象经过点和点 , 当时, , 则的取值范围是( )A、 B、 C、 D、9. 如图,在中,于点 . 分别以为边向外作正方形,得到较大的三个正方形的面积分别为 , 那么最小的正方形面积为( )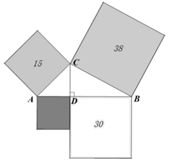 A、5 B、6 C、7 D、10. 如图,在中, , , , 点为上一点,点分别是点关于的对称点,则的最小值是( )
A、5 B、6 C、7 D、10. 如图,在中, , , , 点为上一点,点分别是点关于的对称点,则的最小值是( ) A、 B、 C、4 D、2
A、 B、 C、4 D、2二、填空题
-
11. 已知点A(-2,-3),点A与点B关于y轴对称,则点B的坐标为.12. 命题“直角三角形两锐角互余”的逆命题是: .13. 等腰三角形的一个内角为 , 则它的一个底角的度数为 .14. 如图,直线与直线相交于点 , 则关于的不等式的解为 .
 15. 如图,在中, , 于点 , , , 则 .
15. 如图,在中, , 于点 , , , 则 . 16. 如图,在中, , , 点在上且 , 点是上的动点,连结 , 点分别是和的中点,连结 . 当时,线段的长为 .
16. 如图,在中, , , 点在上且 , 点是上的动点,连结 , 点分别是和的中点,连结 . 当时,线段的长为 .
三、解答题
-
17. 解不等式组: , 并把解表示在数轴上.
 18. 如图,在△ABC和△DBE中,AC=DE,∠2=∠1,∠A=∠D.求证:AB=DB.
18. 如图,在△ABC和△DBE中,AC=DE,∠2=∠1,∠A=∠D.求证:AB=DB. 19. 已知关于的一次函数 . 当时,;当时, .(1)、求的值;(2)、若是该函数图象上的两点,求证: .20. 如图,在中,是钝角.(保留作图痕迹)
19. 已知关于的一次函数 . 当时,;当时, .(1)、求的值;(2)、若是该函数图象上的两点,求证: .20. 如图,在中,是钝角.(保留作图痕迹) (1)、用无刻度的直尺和圆规作的垂直平分线,分别交于点 .(2)、连结 , 若 , 求的度数.21. 某商场销售A , B两种型号智能手机,这两种手机进价和售价如下表:
(1)、用无刻度的直尺和圆规作的垂直平分线,分别交于点 .(2)、连结 , 若 , 求的度数.21. 某商场销售A , B两种型号智能手机,这两种手机进价和售价如下表:型号
A
B
进价(万元/部)
0.44
0.20
售价(万元/部)
0.5
0.25
该商场计划购进A , B两种型号手机共60部进行销售.
(1)、求A , B两种型号手机全部销售后所获利润y(万元)与购进A型手机的数量x的函数关系.提示:利润(售价进价)销售量(2)、若该商场此次用于购进手机的总资金不超过15.6万元.若两种手机都按售价全部售完,问:该商场应该怎样进货,使全部销售后获得的利润最大,最大利润是多少.22. 已知两地相距 , 甲、乙两人沿同一条公路从地出发匀速运动到地,先到地的人原地休息,甲开轿车,乙骑摩托车.已知乙先出发,然后甲再出发.设在这个过程中,甲、乙两人的距离与乙离开地的时间()之间的函数关系如图所示. (1)、第一次相遇的时间在乙出发小时.(2)、求线段对应的函数表达式.(3)、当甲、乙两人只有一人在行驶,且两人相距时,求此时乙行驶的时间.23. 如图,直线与轴、轴分别交于点 , 点 , 点的坐标为 , 点为轴正半轴上的动点,连结 , 过点作直线的垂线交轴于点 , 垂足为点 , 连结 .
(1)、第一次相遇的时间在乙出发小时.(2)、求线段对应的函数表达式.(3)、当甲、乙两人只有一人在行驶,且两人相距时,求此时乙行驶的时间.23. 如图,直线与轴、轴分别交于点 , 点 , 点的坐标为 , 点为轴正半轴上的动点,连结 , 过点作直线的垂线交轴于点 , 垂足为点 , 连结 . (1)、求出两点的坐标;(2)、求证:;(3)、在点的运动过程中,当为等腰三角形时,请直接写出点的坐标.24.
(1)、求出两点的坐标;(2)、求证:;(3)、在点的运动过程中,当为等腰三角形时,请直接写出点的坐标.24. (1)、【问题情境】课外兴趣小组活动时,老师提出了如下问题:
(1)、【问题情境】课外兴趣小组活动时,老师提出了如下问题:如图1,是的中点, , , A , 三点共线.
求证: .
小明在组内经过合作交流,得到解决方法:延长至点 , 使得 , 连结 .
请根据小明的方法思考:由已知和作图能得到 , 依据是( )
A、 B、 C、 D、(2)、由全等三角形、等腰三角形的性质可得 .
【初步运用】如图2,在中,平分 , 为的中点,过点作 , 分别交的延长线和于点、点A . 求证: .(3)、【拓展运用】如图3,在(1)的基础上(即是的中点, , , A , 三点共线),连结 , 若 , 当 , 时,求的长.