辽宁省沈阳市2023-2024学年九年级下学期初数学调研试题

试卷更新日期：2024-03-22 类型：开学考试

进入出卷网下载

一、选择题（共10小题，每小题3分，共30分）

1. 下列计算中，结果是 $m^{8}$ 的是（）

A、 ${(m^{2})}^{4}$ B、 $m^{2} • m^{4}$ C、 $m^{12} \div m^{2}$ D、 $m^{2} + m^{4}$

查看试题解析
2. 如图①所示，在第一个天平上，物体A的质量等于物体B的质量加上物体C的质量；如图②所示，在第二个天平上，物体A的质量加上物体B的质量等于3个物体C的质量．请你判断：与1个物体A的质量相等的物体C的个数为（）

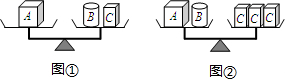A、1 B、2 C、3 D、4

查看试题解析
3. 已知x+y＝3，则点（x，y）一定不在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 函数y＝﹣x²+4x﹣5图象顶点坐标是（）

A、（2，﹣1） B、（﹣2，1） C、（﹣2，﹣1） D、（2，1）

查看试题解析
5. 已知点（﹣2，y₁），（﹣1，y₂），（1，y₃）都在反比例函数y $= \frac{m^{2} + 1}{x}$ 的图象上，那么y₁、y₂、y₃的大小关系是（）

A、y₂＜y₁＜y₃ B、y₃＜y₂＜y₁ C、y₁＜y₂＜y₃ D、y₁＜y₃＜y₂

查看试题解析
6. 正八边形中，每个内角与每个外角的度数之比为（）

A、1：3 B、1：2 C、2：1 D、3：1

查看试题解析
7. 某次乐器比赛共有11名选手参加且他们的得分都互不相同．现在知道这次比赛按选手得分由高到低顺序设置了6个获奖名额．若已知某位选手参加这次比赛的得分，要判断他能否获奖，则下列描述选手比赛成绩的统计量中，只需要知道（）

A、方差 B、平均数 C、众数 D、中位数

查看试题解析
8. 古希腊数学家埃拉托色尼是第一个测算地球周长的人，他在当时的城市塞恩（图中的点A）竖立的杆子在某个时刻没有影子，而此时在500英里以外的亚历山大（图中的点B）竖立杆子的影子却偏离垂直方向约 $7 ° (∠ α \approx 7 °)$ ，由此他得出 $∠ α = ∠ β$ ，那么 $∠ β$ 的度数也就是 $360 °$ 的 $\frac{1}{50}$ ，所以从亚历山大到塞恩的距离也就等于地球周长的 $\frac{1}{50}$ ．其中“ $∠ α = ∠ β$ ”所依据的数学定理是（）

A、两直线平行，内错角相等 B、两直线平行，同位角相等 C、两直线平行，同旁内角互补 D、内错角相等，两直线平行

查看试题解析
9. 如图，方格纸上每个小正方形的边长均为1个单位长度，点O，A，B，C均在格点（两条网格线的交点叫格点）上，以点O为原点建立直角坐标系，则过A，B，C三点的圆的圆心坐标为（）

A、（0，﹣1） B、（﹣1，0） C、（﹣1，﹣1） D、（﹣1，﹣2）

查看试题解析
10. 如图，矩形ABCD中，AB＝6，BC＝8．将矩形ABCD绕点A逆时针旋转90°到矩形AGFE的位置，H是对角线AF的中点，则线段DH的长为（）

A、 $\sqrt{41}$ B、 $2 \sqrt{10}$ C、 $\sqrt{21}$ D、 $2 \sqrt{5}$

查看试题解析

二、填空题（共5小题，每小题3分，共15分）

11. 将160000000用科学记数法表示为．

查看试题解析
12. 若x为有理数，则|x﹣3|+|x﹣2|的最小值为．

查看试题解析
13. 掷一枚质地均匀的硬币，前6次都是正面朝上，则掷第7次时正面朝上的概率是．

查看试题解析
14. 如图，在平面直角坐标系中，直线 $y = \frac{\sqrt{3}}{3} x + 2$ 与x轴交于点A，与y轴交于点B，将△ABO沿直线AB翻折，点O的对应点C恰好落在双曲线 $y = \frac{k}{x} (k \neq 0)$ 上，则k的值为．

查看试题解析
15. 在△ABC中，∠ACB＝90°，∠B＝60°，AB＝8，点D是直线BC上动点，连接AD，在直线AD的右侧作等边△ADE，连接CE，当线段CE的长度最小时，线段CD的长度为．

查看试题解析

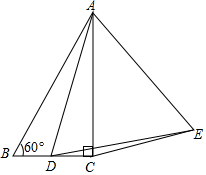
三、解答题（共8小题，共75分）

16.

(1)、解不等式，并将解集在数轴上表示出来：
$\frac{x + 2}{2} - \frac{2 x - 1}{3} ＜ 1$

(2)、计算： $(1 - \sqrt{2})^{0} + (- 1)^{2020} - \sqrt{3} t a n 30 ° + (\frac{1}{3})^{- 2}$ ．

查看试题解析
17. 某校为了解学生对偶像崇拜的情况，从本校学生中随机抽取60名学生，进行问卷调查，并将调查结果收集整理如下：
调查问卷
2023年6月
你崇拜的偶像是（    ）（单选）
A．娱乐明星 B．英雄人物 C．科学家   D．其他
收集数据：
ADCCA DBBAC DBDAC  ACCCC DCADB BCAAC  ACAAC ACCCB BDBDD
整理数据：
崇拜偶像人数统计表
偶像类型
划记
人数
百分比
A．娱乐明星
正正正
15
25%
B．英雄人物
正正下
C．科学家
正正正正正
24
40%
D．其他
9
15%
描述数据：
请根据所统计信息，解答下列问题：

(1)、请补全统计表和条形统计图并填空n＝ ▲ ；

(2)、若该校共有1600名学生，其中崇拜英雄人物和科学家的共约多少人？

(3)、请你针对中学生崇拜偶像问题．提出积极的合理化的建议．

查看试题解析
18. 市政府计划对城区道路进行改造，现安排甲、乙两个工程队共同完成．已知甲队的工作效率是乙队工作效率的1.5倍，甲队改造240米的道路比乙队改造同样长的道路少用2天．

(1)、甲、乙两个工程队每天能改造道路的长度分别是多少米？

(2)、若甲队工作一天的改造费用为7万元，乙队工作一天的改造费用为5万元，如需改造的道路全长为1800米，求安排甲、乙两个工程队同时开工，并一起完成这项城区道路改造的总费用？

查看试题解析
19. 如图是小米洗漱时的侧面示意图.洗漱台（矩形ABCD）靠墙摆放，高AD＝80cm，宽AB＝48cm，小米身高160cm，下半身FG＝100cm，洗漱时下半身与地面成80°（∠FGK＝80°），身体前倾成125°（∠EFG＝125°），脚与洗漱台距离GC＝15cm（点D，C，G，K在同一直线上）.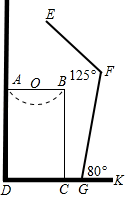

(1)、此时小米头部E点与地面DK相距多少？

(2)、若小米的头部E恰好在洗漱盆AB的中点O的正上方，她应向前或向后移动多少厘米？（sin80°≈0.98，cos80°≈0.18， $\sqrt{2}$ ≈1.41，结果精确到0.1）

查看试题解析
20. 在“新冠病毒”防控期间，某医疗器械公司分两次购进酒精消毒液与测温枪两种商品进行销售，两次购进同一商品的进价相同，具体情况如表所示：
项目
购进数量（件）
购进所需费用（元）
酒精消毒液
测温枪
第一次
40
50
10600
第二次
20
70
14300

(1)、求酒精消毒液和测温枪两种商品每件的进价分别是多少元；

(2)、公司决定酒精消毒液以每件20元出售，测温枪以每件230元出售．为满足市场需求，需购进这两种商品共1000件，且酒精消毒液的数量不少于测温枪数量的4倍，求该公司销售完上述1000件商品获得的最大利润．

查看试题解析
21. 如图， $△ A B C$ 是 $⊙ O$ 的内接三角形，过点C作 $⊙ O$ 的切线交AB的延长线于点D， $O E ⊥ B C$ 于点E，交CD于点F．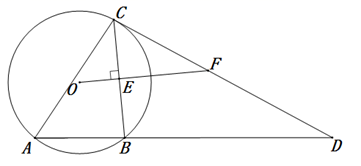

(1)、求证： $∠ A + ∠ O F C = 90 °$ ；

(2)、若 $\tan A = \frac{3}{2} ， B C = 6$ ，求线段CF的长．

查看试题解析
22. 如图，在平面直角坐标系中，抛物线y＝ax²+bx+2过点（1，3），且交x轴于点A（﹣1，0），B两点，交y轴于点C．

(1)、求抛物线的表达式；

(2)、点P是直线BC上方抛物线上的一动点，过点P作PD⊥BC于点D，过点P作y轴的平行线交直线BC于点E，求△PDE周长的最大值及此时点P的坐标；

查看试题解析
23. 在△ABC中，AB＝AC，∠BAC＝α，P为△ABC内的一点．

(1)、如图1，当α＝90°，∠APC＝135°，BP＝5，PC＝3，求AP的长；

(2)、如图2，当α＝90°时，∠BPC＝135°，M为BC的中点，请你写出AP和PM之间的数量关系，并说明理由；

查看试题解析

偶像类型	划记	人数	百分比
A．娱乐明星	正正正	15	25%
B．英雄人物	正正下
C．科学家	正正正正正	24	40%
D．其他		9	15%

项目	购进数量（件）		购进所需费用（元）
项目	酒精消毒液	测温枪	购进所需费用（元）
第一次	40	50	10600
第二次	20	70	14300