2024年浙教版数学八年级下册4.5三角形的中位线课后培优练
试卷更新日期:2024-03-22 类型:同步测试
一、选择题
-
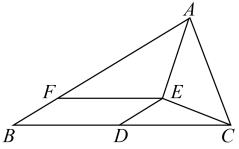
1. 如图,在△ABC中,D,E,F分别是BC,AC,AB的中点若AB=6,BC=8,则四边形BDEF的周长是( )
 A、28 B、14 C、10 D、72. 如图,在△ABC中,∠C=90°,E是CA延长线上-点,F是CB上一点,AE=12,BF=8,点P,Q,D分别是AF ,BE,AB的中点,则PQ的长为( )
A、28 B、14 C、10 D、72. 如图,在△ABC中,∠C=90°,E是CA延长线上-点,F是CB上一点,AE=12,BF=8,点P,Q,D分别是AF ,BE,AB的中点,则PQ的长为( )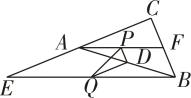 A、 B、4 C、6 D、3. 如图,在中, , 分别是 , 的中点,是上一点, . 若 , , 则的长为( )
A、 B、4 C、6 D、3. 如图,在中, , 分别是 , 的中点,是上一点, . 若 , , 则的长为( ) A、 B、 C、 D、4. 如图,在四边形中,E、F分别是、的中点, , 若 , , 则的长度为( )
A、 B、 C、 D、4. 如图,在四边形中,E、F分别是、的中点, , 若 , , 则的长度为( ) A、6 B、5 C、4 D、35. 如图,在中, , 、、分别是三边的中点, , 则的长为( )
A、6 B、5 C、4 D、35. 如图,在中, , 、、分别是三边的中点, , 则的长为( ) A、 B、 C、 D、6. 如图,在Rt△ABC中,∠C=90°,AC=4,AB=8,点D是AC上一个动点,以AB为对角线的所有平行四边形ADBE中,线段DE的最小值是( )
A、 B、 C、 D、6. 如图,在Rt△ABC中,∠C=90°,AC=4,AB=8,点D是AC上一个动点,以AB为对角线的所有平行四边形ADBE中,线段DE的最小值是( ) A、4 B、 C、 D、67. 如图,在 中, , , 分别是 , 的中点, , 为 上的点,连接 , .若 cm, cm, cm,则图中阴影部分面积为( )
A、4 B、 C、 D、67. 如图,在 中, , , 分别是 , 的中点, , 为 上的点,连接 , .若 cm, cm, cm,则图中阴影部分面积为( )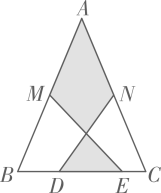 A、25cm2 B、35cm2 C、30cm2 D、42cm28. 如图, 中, ,点 在边 上,且满足 , 为线段 的中点,若 , ,则 ( )
A、25cm2 B、35cm2 C、30cm2 D、42cm28. 如图, 中, ,点 在边 上,且满足 , 为线段 的中点,若 , ,则 ( ) A、 B、 C、 D、6
A、 B、 C、 D、6二、填空题
-
9. 如图,在中, , , , , 分别为 , 上的中点,连接 , , 分别取 , , 的中点 , , , 顺次连接 , , , 则的周长为 .
 10. 在正方形中, , 点在边上,沿直线翻折后点落到正方形的内部点 , 连接、、 , 如图,如果 , 那么 .
10. 在正方形中, , 点在边上,沿直线翻折后点落到正方形的内部点 , 连接、、 , 如图,如果 , 那么 . 11. 如图,在中,于点 , 其中分别是 , , 的中点,下列三个结论:①四边形是平行四边形;②;③ . 其中正确的结论是 . (填上相应的序号即可)
11. 如图,在中,于点 , 其中分别是 , , 的中点,下列三个结论:①四边形是平行四边形;②;③ . 其中正确的结论是 . (填上相应的序号即可) 12. 如图1是雨伞的结构示意图.OP是伞柄,OM,AB,CD是伞骨.已知点A,C分别是OM,AB的中点.CD=(dm),点B,D在OP上滑动时,可将雨伞打开或收拢.当OP与水平面垂直时打开雨伞,雨伞能罩住的水平面大小可近似地看成一个圆.如图2,当雨伞完全打开时,∠ABD=90°;再将雨伞收拢到如图3,此时B′D′=1(dm),且点C′到OP的距离恰好等于图2中BD的长.则伞骨AB的长为 (dm),设图2中能罩住的水平面面积是S1 , 图3中能罩住的水平面面积是S2 , 则= .
12. 如图1是雨伞的结构示意图.OP是伞柄,OM,AB,CD是伞骨.已知点A,C分别是OM,AB的中点.CD=(dm),点B,D在OP上滑动时,可将雨伞打开或收拢.当OP与水平面垂直时打开雨伞,雨伞能罩住的水平面大小可近似地看成一个圆.如图2,当雨伞完全打开时,∠ABD=90°;再将雨伞收拢到如图3,此时B′D′=1(dm),且点C′到OP的距离恰好等于图2中BD的长.则伞骨AB的长为 (dm),设图2中能罩住的水平面面积是S1 , 图3中能罩住的水平面面积是S2 , 则= .
三、解答题
-
13. 下面是证明三角形中位线定理的两种添加辅助线的方法,选择其中一种,完成证明.
三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
已知:如图,在中,点D , E分别是 , 边的中点.求证: , 且 .
 (1)、方法一:证明:如图,延长到点 , 使 , 连接 , , .
(1)、方法一:证明:如图,延长到点 , 使 , 连接 , , .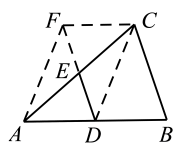 (2)、方法二:证明:如图,取中点 , 连接并延长到点 , 使 , 连接 .
(2)、方法二:证明:如图,取中点 , 连接并延长到点 , 使 , 连接 .