四川省成都市石室名校2024届高三下学期二诊模拟考试 数学(理)
试卷更新日期:2024-03-22 类型:高考模拟
一、选择题(本题共12道小题,每小题5分,共60分)
-
1. 已知复数(其中为虚数单位),则的虚部是( )A、 B、 C、 D、2. 若集合 , 则是的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件3. 如图是根据某校高三8位同学的数学月考成绩(单位:分)画出的茎叶图,其中左边的数字从左到右分别表示学生数学月考成绩的百位数字和十位数字,右边的数字表示学生数学月考成绩的个位数字,则下列结论正确的是( )
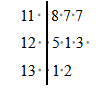 A、这8位同学数学月考成绩的极差是14 B、这8位同学数学月考成绩的中位数是122 C、这8位同学数学月考成绩的众数是118 D、这8位同学数学月考成绩的平均数是1244. 已知一个空间几何体的三视图如图所示,其中正视图、侧视图都是由半圆和矩形组成,则这个几何体的体积是( )
A、这8位同学数学月考成绩的极差是14 B、这8位同学数学月考成绩的中位数是122 C、这8位同学数学月考成绩的众数是118 D、这8位同学数学月考成绩的平均数是1244. 已知一个空间几何体的三视图如图所示,其中正视图、侧视图都是由半圆和矩形组成,则这个几何体的体积是( )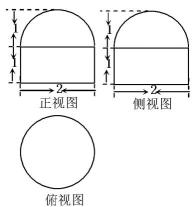 A、 B、 C、 D、5. 已知数列为等差数列,且 , 则的值为( )A、2 B、4 C、6 D、86. 若是正实数,且 , 则的最小值为( )A、 B、 C、 D、7. 当时,关于的不等式有解,则的最小值是( )A、 B、 C、 D、8. 在2023年成都“世界大学生运动会”期间,组委会将甲,乙,丙,丁四位志愿者分配到三个场馆执勤,若每个场馆至少分到一人,且甲不能被分配到场馆,则不同分配方案的种数是( )A、48 B、36 C、24 D、129. 已知抛物线 , 弦过其焦点,分别过弦的端点的两条切线交于点 , 点到直线距离的最小值是( )A、 B、 C、1 D、210. 如图,四棱柱中,为棱的中点,为四边形对角线的交点,下列说法:
A、 B、 C、 D、5. 已知数列为等差数列,且 , 则的值为( )A、2 B、4 C、6 D、86. 若是正实数,且 , 则的最小值为( )A、 B、 C、 D、7. 当时,关于的不等式有解,则的最小值是( )A、 B、 C、 D、8. 在2023年成都“世界大学生运动会”期间,组委会将甲,乙,丙,丁四位志愿者分配到三个场馆执勤,若每个场馆至少分到一人,且甲不能被分配到场馆,则不同分配方案的种数是( )A、48 B、36 C、24 D、129. 已知抛物线 , 弦过其焦点,分别过弦的端点的两条切线交于点 , 点到直线距离的最小值是( )A、 B、 C、1 D、210. 如图,四棱柱中,为棱的中点,为四边形对角线的交点,下列说法: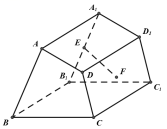
①//平面;
②若//平面 , 则;
③若四边形矩形,且 , 则四棱柱为直四棱柱.
其中正确说法的个数是( )
A、0 B、1 C、2 D、311. 已知函数 , 若 , , , 则( )A、 B、 C、 D、12. 若双曲线的左、右焦点分别为 , 过右焦点的直线与双曲线交于两点,已知的斜率为 , , 且 , , 则直线的斜率是( )A、 B、 C、 D、二、填空题(本题共4道小题,每小题5分,共20分)
-
13. 已知向量 , , 若 , 则实数.14. 已知实数满足约束条件 , 则的最大值是.15. 已知等比数列的前项和为 , 若 , 则取最大值时,的值为 .16. 若 , 恒有 , 则的取值范围是.
三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。
-
17. 为了去库存,某商场举行如下促销活动:有两个摸奖箱,箱内有1个红球、1个黑球、8个白球,箱内有4个红球、4个黑球、2个白球,每次摸奖后放回.消费额满300元有一次箱内摸奖机会,消费额满600元有一次箱内摸奖机会.每次机会均为从箱子中摸出1个球,中奖规则如下:红球奖50元代金券、黑球奖30元代金券、白球奖10元代金券.(1)、某三位顾客各有一次箱内摸奖机会,求中奖10元代金券人数的分布列;(2)、某顾客消费额为600元,请问:这位顾客如何抽奖所得的代金券期望值较大?18. 已知 , 设.(1)、求函数的对称中心;(2)、若中,角所对的边分别为 , , 且外接圆的半径为 , 是边的中点,求线段长度的最大值.19. 如图,棱长为的正方体中,是棱上靠近的三等分点.
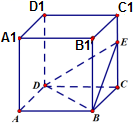 (1)、求证:与平面不垂直;(2)、在线段上是否存在一点使得平面平面?若存在,请计算的值;若不存在,请说明理由.20. 已知点是椭圆的右焦点,过原点的直线交椭圆于两点,面积的最大值为 , .(1)、求椭圆的标准方程;(2)、已知过点的直线与椭圆E交于两点,是否存在定点 , 使得直线的斜率之和为定值?若存在,求出定点的坐标及该定值.若不存在,请说明理由.21. 已知函数(1)、是否存在实数使得在区间上恒成立,若存在,求出的取值范围,若不存在,请说明理由;(2)、求函数在区间上的零点个数(为自然对数的底数).
(1)、求证:与平面不垂直;(2)、在线段上是否存在一点使得平面平面?若存在,请计算的值;若不存在,请说明理由.20. 已知点是椭圆的右焦点,过原点的直线交椭圆于两点,面积的最大值为 , .(1)、求椭圆的标准方程;(2)、已知过点的直线与椭圆E交于两点,是否存在定点 , 使得直线的斜率之和为定值?若存在,求出定点的坐标及该定值.若不存在,请说明理由.21. 已知函数(1)、是否存在实数使得在区间上恒成立,若存在,求出的取值范围,若不存在,请说明理由;(2)、求函数在区间上的零点个数(为自然对数的底数).四、选考题:共10分。请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。[选修4-4:坐标系与参数方程](10分)