【培优卷】2024年浙教版数学七年级下册3.7整式的除法同步练习

试卷更新日期：2024-03-21 类型：同步测试

进入出卷网下载

一、选择题

1. 计算 $(- x^{5} + 3 x^{3} - M) \div (- 3 x) = \frac{1}{3} x^{4} - x^{2} + 2 x$ ，那么M=（）．

A、-3x B、 $3 x^{2}$ C、 $6 x^{2}$ D、 $- 6 x^{2}$

查看试题解析
2. 计算（-8m⁴n+12m³n²-4m²n³）÷（-4m²n）的结果是（　）

A、2m²n-3mn+n² B、2n²-3mn²+n² C、2m²-3mn+n² D、2m²-3mn+n

查看试题解析
3. 已知 $a \neq 0$ ，给出四个代数式，其中有一个代数式与其余代数式的化简结果不相等，则这个代数式是（）

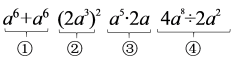A、① B、② C、③ D、④

查看试题解析
4. 下列运算中，正确的是（）

A、 ${(- 2 x^{2} y)}^{3} = - 6 x^{6} y^{3}$ B、 ${(- 4)}^{- 2} = \frac{1}{16}$ C、 $5 x (x^{2} + 2 x y) = 5 x^{2} + 10 x y$ D、 $(4 x^{6} - 2 x^{2} y) \div 2 x^{2} = 2 x^{3} - x y$

查看试题解析
5. 长方形面积是3a²-3ab+6a，一边长为3a，则它的周长为（）

A、2a-b+2 B、8a-2b C、8a-2b+4 D、4a-b+2

查看试题解析
6. 墨迹污染了等式32x³4x＝8x²（x≠0）中的运算符号，则污染的是（）

A、+ B、- C、× D、÷

查看试题解析
7. 若8a³b^m÷（28aⁿb²）= $\frac{2}{7}$ b² ，则m，n的值为（）

A、m=2，n=3 B、m=1，n=3 C、m=4，n=3 D、m=4，n=1

查看试题解析
8. 下列计算：①a⁹÷（a⁷÷a）=a³；②3x²yz÷（-xy）=-3xz；③（10x³-16x²+2x）÷（2x）=5x²-8x；④（a-b）⁹÷（a-b）⁶=a³-b³中，其中运算结果错误的是（）

A、①② B、③④ C、①④ D、②③

查看试题解析

二、填空题

9. 若一个多项式与 $- \frac{1}{2} m n$ 的乘积为 $3 m^{2} n - m n^{2} + \frac{1}{2} m n$ ，则这个多项式为．

查看试题解析
10. 多项式A与单项式2x的积为 $2 x^{2} + 14 x$ ，则 $A =$ ．

查看试题解析
11. 若关于x的多项式 $(17 x^{2} - 3 x + 4) - (a x^{2} + b x + c)$ 除以 $5 x$ ，所得商恰好为 $2 x + 1$ ，则 $a + b + c =$ .

查看试题解析
12. 如图，一个长、宽、高分别为a，b， $2 r$ 的长方体纸盒装满了一层半径为r的小球，则纸盒的空间利用率（小球总体积与纸箱容积的比）为（结果保留 $π$ ，球体积公式 $V = \frac{4}{3} π r^{3}$ ）．

查看试题解析

三、解答题

13. 先化简再求值： $(- 2 x^{3} - 6 x) \div (- 2 x) - 2 (3 x + 1) (3 x - 1) + 7 x (x - 1)$ ，其中 $x = - 3$ ．

查看试题解析
14. 某天数学课上，小明学习了整式的除法运算，放学后，小明回到家拿出课堂笔记，认真地复习课上学习的内容.他突然发现一道三项式除法运算题：（21x⁴y³-+7x²y²）÷（-7x²y）=+5xy-y，被除式的第二项被墨水弄污了，商的第一项也被墨水弄污了，你能算出两处被污染的内容是什么吗?

查看试题解析
15. 我们已经学习过多项式除以单项式，多项式除以多项式一般可用竖式计算，步骤如下：
①把被除式、除式按某个字母作降幂接列，井把所块的项用零补齐；

②用除式的第一项除以除式第一项，得到商式的第一项；

③用商式的一项去乘除式，把积写在被除式下面（同类项对齐），消去相等项；

④把减得的差当作新的被除式，再按照上面的方法继续演算，直到余式为零或余式的次数低于除式的次数时为止，被除式＝除式×商式+余式，若余式为零，说明这个多项式能被另一个多项式整除.

例如：计算（6x⁴﹣7x³﹣x²﹣1）÷（2x+1），可用竖式除法如图：

所以6x⁴﹣7x³﹣x²﹣1除以2x+1，商式为3x³﹣5x²﹣2x﹣1，余式为0.

根据阅读材料，请回答下列问题：

(1)、（x³﹣4x²+7x﹣5）÷（x﹣2）的商是，余式是；

(2)、x³﹣x²+ax+b能被x²+2x+2整除，求a，b的值.

查看试题解析

【培优卷】2024年浙教版数学七年级下册3.7整式的除法 同步练习

一、选择题

二、填空题

三、解答题

【培优卷】2024年浙教版数学七年级下册3.7整式的除法同步练习