广西桂林市2023-2024学年高二下学期开学考试数学试卷

试卷更新日期：2024-03-21 类型：开学考试

进入出卷网下载

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 甲同学计划分别从3份不同的语文试卷、5份不同的数学试卷中各任选1份试卷练习，则不同的选法共有（）

A、8种 B、15种 C、 $3^{5}$ 种 D、 $5^{3}$ 种

查看试题解析
2. 双曲线 $E$ ： $\frac{x^{2}}{3} - \frac{y^{2}}{6} = 1$ 的渐近线方程为（）

A、 $\sqrt{2} x \pm y = 0$ B、 $x \pm \sqrt{2} y = 0$ C、 $\sqrt{3} x \pm y = 0$ D、 $x \pm \sqrt{3} y = 0$

查看试题解析
3. 下列四对向量中，垂直的是（）

A、 $\vec{a} = (2 ， 0 ， 1)$ ， $\vec{b} = (- 1 ， 1 ， - 2)$ B、 $\vec{a} = (2 ， 1 ， 3)$ ， $\vec{b} = (- 1 ， - 1 ， 1)$ C、 $\vec{a} = (4 ， 0 ， 6)$ ， $\vec{b} = (2 ， 0 ， 3)$ D、 $\vec{a} = (3 ， 1 ， 1)$ ， $\vec{b} = (- 1 ， - 2 ， 2)$

查看试题解析
4. ${(\frac{1}{x} - 2 x^{2})}^{9}$ 的展开式中，常数项为（）

A、-672 B、672 C、-144 D、144

查看试题解析
5. 对两个变量的三组数据进行统计，得到以下散点图，关于两个变量相关系数的比较，正确的是（）

A、 $r_{1} > r_{2} > r_{3}$ B、 $r_{2} > r_{3} > r_{1}$ C、 $r_{1} > r_{3} > r_{2}$ D、 $r_{3} > r_{2} > r_{1}$

查看试题解析
6. 在四面体 $A B C D$ 中， $\vec{B M} = 2 \vec{M C} ， \vec{A N} = \vec{N D}$ ，则 $\vec{M N} =$ （）

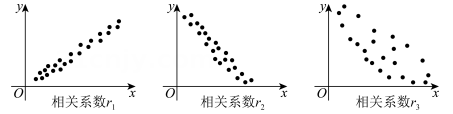A、 $\frac{1}{3} \vec{A B} + \frac{2}{3} \vec{A C} + \frac{1}{2} \vec{A D}$ B、 $\frac{1}{3} \vec{A B} + \frac{2}{3} \vec{A C} - \frac{1}{2} \vec{A D}$ C、 $- \frac{1}{3} \vec{A B} - \frac{2}{3} \vec{A C} + \frac{1}{2} \vec{A D}$ D、 $- \frac{1}{3} \vec{A B} + \frac{2}{3} \vec{A C} + \frac{1}{2} \vec{A D}$

查看试题解析
7. 从甲、乙等12人中任选5人，则甲、乙至多有1人被选中的选法共有（）

A、252种 B、420种 C、672种 D、10080种

查看试题解析
8. 已知直线 $l_{1}$ ： $m x + y + 4 = 0$ 与直线 $l_{2}$ ： $x - m y - 6 - 4 m = 0$ 交于点 $P (x_{0} ， y_{0})$ ，则 $x_{0}^{2} + y_{0}^{2}$ 的最大值为（）

A、4 B、8 C、32 D、64

查看试题解析

二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.

9. 已知随机变量 $X \sim N (12 ， σ^{2})$ ，且 $P (X < 10) = 0.2$ ，则下列说法正确的是（）

A、 $P (X > 14) = 0.2$ B、 $P (10 \leq X \leq 14) = 0.6$ C、若 $Y = 3 X + 1$ ，则 $E Y = 36$ D、若 $Y = 3 X + 1$ ，则 $D Y = 9 σ^{2}$

查看试题解析
10. 已知直线 $l$ ： $x + \sqrt{3} y + c = 0 (c \neq 0)$ ， $O$ 为坐标原点，则（）

A、直线 $l$ 的倾斜角为 $120 °$ B、若 $O$ 到直线 $l$ 的距离为 $1$ ，则c＝2 C、过 $O$ 且与直线 $l$ 平行的直线方程为 $x + \sqrt{3} y = 0$ D、过 $O$ 且与直线 $l$ 垂直的直线方程为 $\sqrt{3} x - y = 0$

查看试题解析
11. 若曲线 $C_{1} ： y = k | x | + 2$ 与曲线 $C_{2} ： \frac{x^{2}}{2} + y | y | = 1$ 有6个公共点，则 $k$ 的值可能是（）

A、 $- \frac{\sqrt{15}}{3}$ B、 $- \frac{\sqrt{10}}{2}$ C、 $- \frac{\sqrt{7}}{2}$ D、 $- \sqrt{2}$

查看试题解析

三、填空题：本题共3小题，每小题5分，共15分.

12. 直线 $l_{1}$ ： $a x + 2 y - 3 = 0$ ， $l_{2}$ ： $2 x + a y + a + 5 = 0$ ，若 $l_{1} / / l_{2}$ ，则 $a =$ .

查看试题解析
13. 已知抛物线 $E ： y^{2} = 8 x$ 的焦点为 $F$ ， $M (x_{0} ， y_{0})$ 是 $E$ 上一点，且 $| M F | = \frac{4 x_{0}}{3}$ ，则 $x_{0} =$ ．

查看试题解析
14. $2^{2024}$ 被9除的余数为.

查看试题解析

四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.

15. 已知圆C上有两个点A $(2 ， 3)$ ， B $(4 ， 9)$ ，且AB为直径．

(1)、求圆C的方程；

(2)、已知P $(0 ， 5)$ ，求过点P且与圆C相切的直线方程．

查看试题解析
16. 下表是某社区男、女居民对附近商场体验感评价的调查结果（单位：人）.
评价
居民
评价高
评价一般
总计
男居民
30
女居民
35
总计
45
100

(1)、完善上述表格数据，试问是否有 $99 %$ 的把握判断体验感评价与性别有关？

(2)、从评价高的居民中按性别采用分层随机抽样的方法选取6人，再从这6人中任选3人进行深度调查，记进行深度调查的男居民的人数为 $X$ ，求 $X$ 的分布列与期望.
附： $χ^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ， $n = a + b + c + d$ .
当 $χ^{2} \leq 2.706$ 时，没有充分的证据判断变量 $A$ ， $B$ 有关联，可以认为变量 $A$ ， $B$ 是没有关联的；
当 $χ^{2} > 2.706$ 时，有 $90 %$ 的把握判断变量 $A$ ， $B$ 有关联；
当 $χ^{2} > 3.841$ 时，有 $95 %$ 的把握判断变量 $A$ ， $B$ 有关联；
当 $χ^{2} > 6.635$ 时，有 $99 %$ 的把握判断变量 $A$ ， $B$ 有关联.

查看试题解析
17. 如图，四棱锥 $P - A B C D$ 的底面 $A B C D$ 是平行四边形， $△ P A B$ 是边长为2的正三角形，平面 $P A B ⊥$ 平面 $A B C D ， ∠ A B C = \frac{π}{3} ， B C = 4 ， E$ 为棱 $P D$ 的中点．

(1)、证明： $A C ⊥$ 平面 $P A B$ ．

(2)、求直线 $B E$ 与平面 $P A C$ 所成角的正弦值．

查看试题解析
18. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{3}}{3}$ ，且椭圆 $C$ 的短轴长为 $2 \sqrt{6}$ ．

(1)、求椭圆 $C$ 的方程．

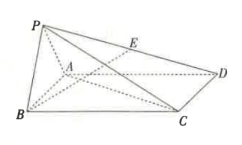(2)、设 $P$ 是椭圆 $C$ 上第一象限内的一点， $A$ 是椭圆 $C$ 的左顶点， $B$ 是椭圆 $C$ 的上顶点，直线 $P A$ 与 $y$ 轴相交于点 $M$ ，直线 $P B$ 与 $x$ 轴相交于点 $N$ ．记 $△ A B N$ 的面积为 $S_{1}$ ， $△ A M N$ 的面积为 $S_{2}$ ．证明： $| S_{1} - S_{2} |$ 为定值．

查看试题解析
19. 某学校食堂每天中午为师生提供了冰糖雪梨汤和苹果百合汤，其均有止咳润肺的功效．某同学每天中午都会在两种汤中选择一种，已知他第一天选择冰糖雪梨汤的概率为 $\frac{2}{3}$ ，若前一天选择冰糖雪梨汤，则后一天继续选择冰糖雪梨汤的概率为 $\frac{1}{3}$ ，而前一天选择苹果百合汤，后一天继续选择苹果百合汤的概率为 $\frac{1}{2}$ ，如此往复．

(1)、求该同学第二天中午选择冰糖雪梨汤的概率．

(2)、记该同学第 $n$ 天中午选择冰糖雪梨汤的概率为 $P_{n}$ ，证明： ${P_{n} - \frac{3}{7}}$ 为等比数列．

(3)、求从第1天到第10天中，该同学中午选择冰糖雪梨汤的概率大于苹果百合汤概率的天数．

查看试题解析

评价居民	评价高	评价一般	总计
男居民	30
女居民		35
总计	45		100