云南省下关重点中学2023-2024学年高一下学期开学考试数学试题
试卷更新日期:2024-03-21 类型:开学考试
一、单项选择题:本题共8小题,每小题满分5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求,选对得5分,选错得0分.
-
1. 已知集合A={x|1<x<4},B={x|x≤2},则A∩B等于( )A、(0,1) B、(0,2] C、(1,2) D、(1,2]2. 命题:“∀x∈(-1,1),都有x2<1”的否定是( )A、∀x∈(-1,1),都有x2≥1 B、∀x∉(-1,1),都有x2≥1 C、∃x∈(-1,1),使得x2≥1 D、∃x∉(-1,1),使得x2≥13. 函数f(x)=的定义域为( )A、{x|x≥-3且x≠-1} B、{x|x>-3且x≠-1} C、{x|x≥-1} D、{x|x≥-3}4. , , ,则 的大小关系为( )A、 B、 C、 D、5. 函数的部分图象大致为( )A、
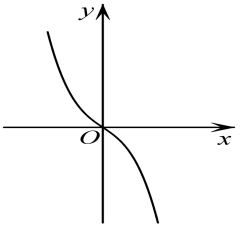 B、
B、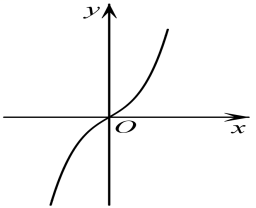 C、
C、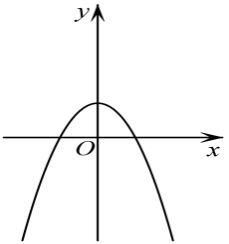 D、
D、 6. 函数f(x)=sin 2x+cos 2x的最小正周期为( )A、 B、 C、π D、2π7. 函数f(x)=log3x+x3-9的零点所在区间是( )A、(0,1) B、(1,2) C、(2,3) D、(3,4)8. 设、、依次表示函数 , , 的零点,则、、的大小关系为( ).A、 B、 C、 D、
6. 函数f(x)=sin 2x+cos 2x的最小正周期为( )A、 B、 C、π D、2π7. 函数f(x)=log3x+x3-9的零点所在区间是( )A、(0,1) B、(1,2) C、(2,3) D、(3,4)8. 设、、依次表示函数 , , 的零点,则、、的大小关系为( ).A、 B、 C、 D、二、多项选择题:本题共4小题,每小题满分5分,共20分. 在每小题给出的四个选项中,有多项符合题目要求。全部选对得5分,部分选对得2分,有选错的得0分.
-
9. 下列结论正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则10. 下列各式中,值为的是( )A、 B、 C、 D、11. 将函数的图象向左平移个单位长度,得到函数的图象,则函数具有以下哪些性质( )A、最大值为 , 图象关于直线对称 B、图象关于y轴对称 C、最小正周期为 D、图象关于点成中心对称12. 设函数 , 若 , 且 , 则的值可以是( )A、4 B、5 C、 D、6
三、填空题:本题共4小题,每小题5分,共20分。
-
13. log24+log42=.14. 设 , , ,则 的最小值为 .15. 已知 , 则.16. 设函数在区间上的最大值为M,最小值为N,则 的值为.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
-
17. 已知集合 , 集合.(1)、若是的必要不充分条件,求实数的取值范围;(2)、若 , 求实数的取值范围.
(2【答案】
18. 已知函数 .(1)、求函数的对称中心;(2)、当时,求函数的值域.19. 在 中,内角 的对边分别为 .已知(1)、求 的值(2)、若 ,求 的面积.20. 某手机生产商计划在2023年利用新技术生产某款新手机,通过市场分析,生产此款手机全年需投入固定成本200万元,每生产(千部)手机,需另投人成本万元,且 , 由市场调研知,每部手机售价0.5万元,且全年内生产的手机当年能全部销售完.(1)、求出2023年的利润(万元)关于年产量(千部)的函数关系式;(利润销售额成本)(2)、2023年产量为多少千部时,该生产商所获利润最大?最大利润是多少?