广东省茂名市化州市2023-2024学年八年级上学期期末数学试题

试卷更新日期：2024-03-21 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分，在每小题给出四个选项中，其中只有一个是正确的，把选出的答案填涂在答题卡上）

1. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{2}$ B、 $\sqrt{12}$ C、 $\sqrt{\frac{1}{2}}$ D、 $\sqrt{9}$

查看试题解析
2. 以下列长度的三条线段为边，能组成直角三角形的是（　　）

A、2，3，4 B、3， $\sqrt{7}$ ， 5 C、5，12，13 D、4，4，8

查看试题解析
3. 下列运算正确的是（）

A、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ B、 $(2 \sqrt{3})^{2} = 6$ C、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ D、 $\sqrt{(- 2)^{2}} = - 2$

查看试题解析
4. 在平面直角坐标系中，点P（﹣3，2）关于x轴的对称点的坐标为（）

A、（2，﹣3） B、（﹣2，3） C、（﹣3，2） D、（﹣3，﹣2）

查看试题解析
5. 在一次射击比赛中，甲、乙两名运动员10次射击的平均成绩都是9环，其中甲成绩的方差为1.21，乙成绩的方差为3.98，由此可知（）

A、甲比乙的成绩稳定 B、乙比甲的成绩稳定 C、甲、乙两人的成绩一样稳定 D、无法确定谁的成绩更稳定

查看试题解析
6. 在一次体育测试中，小芳所在小组8人的成绩分别是：46，47，48，48，50，49，49，49．则这8人体育成绩的中位数、众数分别是（）

A、47 ，49 B、48 ，50 C、48.5 ，49 D、49，48

查看试题解析
7. 对于函数 $y = - 2 x + 4$ ，说法正确的是(　　)

A、点 $A (1 ， 3)$ 在这个函数图象上 B、 $y$ 随着 $x$ 的增大而增大 C、它的图象必过一、三象限 D、当 $x > 2$ 时， $y < 0$

查看试题解析
8. 如图，已知 $a ⊥ c$ ， $b ⊥ c$ ，若 $∠ 1 = 65 °$ ，则 $∠ 2$ 等于（）

A、65° B、90° C、25° D、70°

查看试题解析
9. 《孙子算经》中有一道题，原文是：“今有木，不知长短，引绳度之，余绳四尺五寸：屈绳量之，不足一尺，木长几何？”意思是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长水，长木还剩余1尺，问木长多少尺。设木长为x尺，绳子长为y尺，则下列符合题意的方程组是（）

A、 ${\begin{array}{l} y = x + 4.5 \\ \frac{1}{2} y = x + 1 \end{array}$ B、 ${\begin{array}{l} y = x + 4.5 \\ \frac{1}{2} y = x - 1 \end{array}$ C、 ${\begin{array}{l} y = 4.5 - x \\ \frac{1}{2} y = x + 1 \end{array}$ D、 ${\begin{array}{l} y = x - 4.5 \\ \frac{1}{2} y = x - 1 \end{array}$

查看试题解析
10. 已知，如图长方形 $A B C D$ 中， $A B = 3 c m ， A D = 9 c m$ ，将此长方形折叠，使点B与点D重合，折痕为 $E F$ ，则 $△ A B E$ 的面积为（　　）

A、3 $c m^{2}$ B、4 $c m^{2}$ C、6 $c m^{2}$ D、 $12$ $c m^{2}$

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分，请将下列各题的正确答案写在答题卡相应的位置上）

11. 若点 $A (- 2 ， y_{1})$ ， $B (1 ， y_{2})$ 都在一次函数 $y = - x + b$ 的图象上，则 $y_{1}$ $y_{2}$ （用“＞”，“＜”或“＝”填空）．

查看试题解析
12. 在平面直角坐标系 $x O y$ 中，一次函数 $y = k x$ 和 $y = - x + 3$ 的图象如图所示，则二元一次方程组 ${\begin{array}{l} k x = y \\ - x + 3 = y \end{array}$ 的解为．

查看试题解析
13. 某射击队准备挑选运动员参加射击比赛．下表是其中一名运动员10次射击的成绩（单位：环）：
成绩
7.5
8.5
9
10
频数
2
2
3
3
则该名运动员射击成绩的平均数是环．

查看试题解析
14. 如图，每个小正方形的边长都相等， $A$ ， $B$ ， $C$ 是小正方形的顶点，则 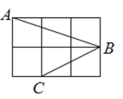$∠ A B C$ 的度数为．

查看试题解析
15. 如图，将三角板的直角顶点放在直尺的一边上，∠1=30°，∠2=50°，则∠3=°。

查看试题解析
16. 规定用符号 $[m]$ 表示一个实数 $m$ 的整数部分，例如： $[\frac{2}{3}] = 0$ ， $[3.14] = 3$ ，按此规定 $[7 - \sqrt{5}]$ 的值为．

查看试题解析

三、解答题（本大题共9小题，满分72分，解答应写出文字说明、证明过程或演算步骤）

17. 解方程组： ${\begin{array}{l} x - y = 1 ① \\ 5 x + y = 11 ② \end{array}$

查看试题解析
18. 已知一次函数 $y = k x + b$ 的图象经过点 $(- 2 ， 1)$ ，且与y轴的交点的纵坐标为3．求一次函数的解析式．

查看试题解析
19. 如图所示，在 $△ A B C$ 中， $∠ A = 62 °$ ， $∠ B = 74 °$ ， $C D$ 是 $∠ A C B$ 的角平分线，点E在 $A C$ 上， $D E ∥ B C$ ，求 $∠ C D E$ 的度数．

查看试题解析
20. 阅读下列材料，然后回答问题．
在进行二次根式运算时，我们有时会碰上 $\frac{2}{\sqrt{3} + 1}$ 这样的式子，其实我们还可以将其进一步化简： $\frac{2}{\sqrt{3} + 1} = \frac{2 \times (\sqrt{3} - 1)}{(\sqrt{3} + 1) \times (\sqrt{3} - 1)} = \frac{2 \times (\sqrt{3} - 1)}{{(\sqrt{3})}^{2} - 1^{2}} = \sqrt{3} - 1 ．$
以上这种化简的步骤叫作分母有理化．
化简： $\frac{2}{\sqrt{5} + \sqrt{3}}$ ．

查看试题解析
21. 围棋，起源于中国，古代称为“弈”，是棋类鼻祖，距今已有4000多年的历史．如图是某围棋棋盘的局部，若棋盘是由边长均为1的小正方形组成的，棋盘上A、B两颗棋子的坐标分别为 $A (- 2 ， 4)$ ， $B (1 ， 2)$ ．

(1)、根据题意，画出相应的平面直角坐标系；

(2)、分别写出C、D两颗棋子的坐标；

(3)、有一颗黑色棋子E的坐标为 $(3 ， - 1)$ ，请在图中画出黑色棋子E ．

查看试题解析
22. 列出方程组解应题．小红打算买一束百合和康乃馨组合的鲜花，在“母亲节”送给妈妈．已知买2支康乃馨和3支百合共需花费 $28$ 元，买3支康乃馨和2支百合共需花费 $27$ 元．

(1)、求买一支康乃馨和一支百合各需多少元？

(2)、小红准备买康乃馨和百合共9支．设买这束鲜花所需费用为 $w$ 元，康乃馨有 $x$ 支，求 $w$ 与 $x$ 之间的函数关系式．

查看试题解析
23. 某校八年级（1）班 $20$ 名学生某次数学测验的成绩统计如表：
成绩 $($ 分 $)$
$60$
$70$
$80$
$90$
$100$
人数 $($ 人 $)$
$1$
$5$
$x$
$y$
$2$

(1)、若这 $20$ 名学生成绩的平均数为 $82$ 分，求 $x$ 和 $y$ 的值．

(2)、在（1）的条件下，求这 $20$ 名学生本次测验成绩的众数和中位数．

查看试题解析
24. 在 $△ A B C$ 中， $∠ B A C = 60 °$ ， $∠ A C B = 2 ∠ B$ ， $A D$ 平分 $∠ B A C$ 交 $B C$ 于点D ．

(1)、求 $∠ B$ 的度数；

(2)、如图①，若 $C E ⊥ A D$ 于点F ，交 $A B$ 于点E ．求 $∠ E C D$ 的度数；

(3)、如图②，若 $C E$ 平分 $∠ A C B$ 交 $A B$ 于点E ，交 $A D$ 于点F ，求 $∠ A F C$ 的度数．

查看试题解析
25. 如图1，在平面直角坐标系 $x O y$ 中，直线 $y = k x + b$ 分别与x轴，y轴交于点 $A (- 1 ， 0)$ ， $B (0 ， 2)$ ，过点 $C (2 ， 0)$ 作x轴的垂线，与直线 $A B$ 交于点D ．

(1)、求点D的坐标；

(2)、点 $E$ 是线段 $C D$ 上一动点，直线 $B E$ 与 $x$ 轴交于点 $F$ ．若 $△ B D F$ 的面积为8，求点F的坐标．

查看试题解析

成绩 $($ 分 $)$	$60$	$70$	$80$	$90$	$100$
人数 $($ 人 $)$	$1$	$5$	$x$	$y$	$2$

成绩	7.5	8.5	9	10
频数	2	2	3	3