贵州省安顺市关岭布依族苗族自治县2023-2024学年八年级上学期期末数学试题
试卷更新日期:2024-03-21 类型:期末考试
一、选择题(本大题共12小题,每小题3分,共36分.在每小题所给的四个选项中,有且只有一项是符合题目要求的)
-
1. 计算:( )A、0 B、1 C、 D、92. 把分解因式,应提取的公因式是( )A、 B、 C、 D、3. 在中, , , 若的长为整数,则的长不可能是( )A、3 B、5 C、7 D、94. 下面是某APP使用界面的部分图标,其中轴对称图形共有( )
 A、1个 B、2个 C、3个 D、4个5. 华夏飞天续锦章,摘星揽月入天阊.2023年10月26日神舟十七号载人飞船在酒泉卫星发射中心圆满发射成功.此次神舟十七号载人飞船航天员空间站还将进行一系列科学实验,包括“空间蛋白质分子组装与应用研究”.其中某一蛋白质分子的直径仅米,这个数用科学记数法表示为( )A、 B、 C、 D、6. 如图,用直尺和圆规过直线l外一点P作直线l的平行线,能得出的依据是( )
A、1个 B、2个 C、3个 D、4个5. 华夏飞天续锦章,摘星揽月入天阊.2023年10月26日神舟十七号载人飞船在酒泉卫星发射中心圆满发射成功.此次神舟十七号载人飞船航天员空间站还将进行一系列科学实验,包括“空间蛋白质分子组装与应用研究”.其中某一蛋白质分子的直径仅米,这个数用科学记数法表示为( )A、 B、 C、 D、6. 如图,用直尺和圆规过直线l外一点P作直线l的平行线,能得出的依据是( )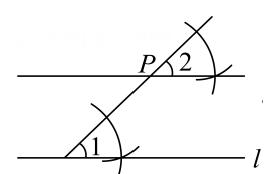 A、 B、 C、 D、7. 如图,点在内部的一条射线上,于点 , 且 . 已知点到射线的最小距离为4,且 , 则的度数为( )
A、 B、 C、 D、7. 如图,点在内部的一条射线上,于点 , 且 . 已知点到射线的最小距离为4,且 , 则的度数为( )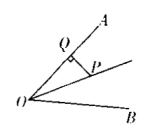 A、 B、 C、 D、8. 若一个多边形的内角和比它的外角和的3倍大 , 则这个多边形的边数是( )A、6 B、7 C、8 D、99. 若关于的方程无解,则的值为( )A、0或1 B、 C、0或 D、或110. 多项式加上一个数或单项式后,使它成为一个多项式的完全平方,那么加上的数或单项式可以从① , ② , ③ , ④ , ⑤中选取,则选取的是( )A、① B、③ C、②③⑤ D、①②③④⑤11. 如图,中, , D是的中点,的垂直平分线分别交、、于点E、O、F , 则图中全等的三角形的对数是( )
A、 B、 C、 D、8. 若一个多边形的内角和比它的外角和的3倍大 , 则这个多边形的边数是( )A、6 B、7 C、8 D、99. 若关于的方程无解,则的值为( )A、0或1 B、 C、0或 D、或110. 多项式加上一个数或单项式后,使它成为一个多项式的完全平方,那么加上的数或单项式可以从① , ② , ③ , ④ , ⑤中选取,则选取的是( )A、① B、③ C、②③⑤ D、①②③④⑤11. 如图,中, , D是的中点,的垂直平分线分别交、、于点E、O、F , 则图中全等的三角形的对数是( )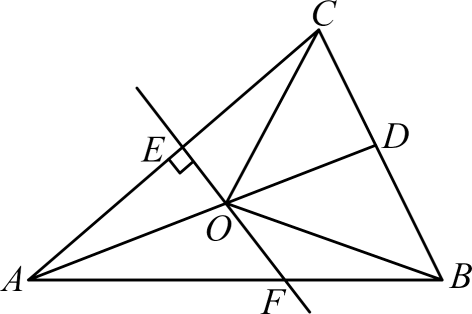 A、2对 B、3对 C、4对 D、5对12. 如图,△为直角三角形, , AD为∠CAB的平分线,与∠ABC的平分线BE交于点E , BG是△ABC的外角平分线,AD与BG相交于点G , 则∠ADC与∠GBF的和为( )
A、2对 B、3对 C、4对 D、5对12. 如图,△为直角三角形, , AD为∠CAB的平分线,与∠ABC的平分线BE交于点E , BG是△ABC的外角平分线,AD与BG相交于点G , 则∠ADC与∠GBF的和为( )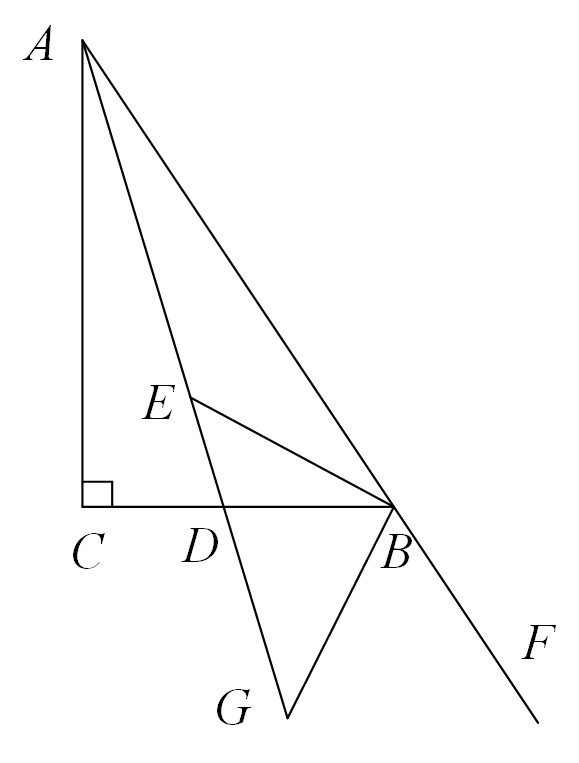 A、120° B、135° C、150° D、160°
A、120° B、135° C、150° D、160°二、填空题(本大题共4小题,每小题4分,共16分)
-
13. 如图,学校门口设置的移动拒马都用钢管焊接成三角形,这样做的数学原理是 .
 14. 如图,一棵树在离地面3米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为米.
14. 如图,一棵树在离地面3米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为米. 15. 如图,线段 , 的垂直平分线相交于点O , 连接 , . 若 , 则的度数为 .
15. 如图,线段 , 的垂直平分线相交于点O , 连接 , . 若 , 则的度数为 .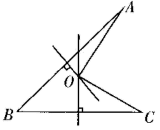 16. 若 , 则的值为 .
16. 若 , 则的值为 .三、解答题(本大题共9小题,共98分.解答时应写出必要的文字说明、证明过程或演算步骤)
-
17.(1)、计算:;(2)、因式分解: .18. 在平面直角坐标系中,的位置如图所示.
 (1)、点A关于轴对称的点在第四象限;(填“”或“”)(2)、画出与关于y轴对称的;(3)、在x轴上作一点P , 使其到点B , C的距离之和最小.(不写作法,保留作图痕迹)19. 先化简: , 再从 , 0,1中选择一个合适的数作为x的值代入求值.20. 周末,小明和小玮去公园玩,他们发现一个人工湖,喜欢思考的小明对小玮说:“老师说,我们要用数学的眼光看世界,那么,你能用我们学过的数学知识测量出湖的宽度(以最宽处计算)吗?”小玮观察了一下,给出了如下测量方案.
(1)、点A关于轴对称的点在第四象限;(填“”或“”)(2)、画出与关于y轴对称的;(3)、在x轴上作一点P , 使其到点B , C的距离之和最小.(不写作法,保留作图痕迹)19. 先化简: , 再从 , 0,1中选择一个合适的数作为x的值代入求值.20. 周末,小明和小玮去公园玩,他们发现一个人工湖,喜欢思考的小明对小玮说:“老师说,我们要用数学的眼光看世界,那么,你能用我们学过的数学知识测量出湖的宽度(以最宽处计算)吗?”小玮观察了一下,给出了如下测量方案.
如图,首先在湖两岸相对的地方选取两点两点之间的距离就是湖的宽度.要测量湖两岸相对的两点间的距离,可以在湖外取的垂线上的两点 , 使 , 再画出的垂线 , 使点与点在同一条直线上.若想知道两点之间的距离,只需要测量出线段的长度即可.请你用学过的数学知识来说明小玮的做法是否正确.
21. 如图所示,已知AD,AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.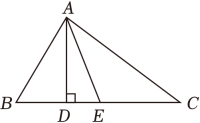 (1)、求AD的长;(2)、求△ACE和△ABE周长的差.22. 某居民小组正在进行美丽乡村建设,为了提升居民的幸福指数,现规划将一块长、宽的长方形场地(如图)打造成居民健身场所,具体规划为:在这块场地中分割出一块长、宽的长方形场地建篮球场,其余的地方安装各种健身器材.
(1)、求AD的长;(2)、求△ACE和△ABE周长的差.22. 某居民小组正在进行美丽乡村建设,为了提升居民的幸福指数,现规划将一块长、宽的长方形场地(如图)打造成居民健身场所,具体规划为:在这块场地中分割出一块长、宽的长方形场地建篮球场,其余的地方安装各种健身器材.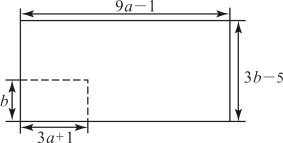 (1)、求安装健身器材的区域面积;(2)、当 , 时,求安装健身器材的区域面积.23. 某校为迎接市中学生田径运动会需准备240面彩旗.计划由八年级一班的3个小组完成此任务,3个小组的人数相等.后因1个小组另有任务,剩余2个小组的每名学生要比原计划多做4面彩旗才能完成任务,那么每个小组有多少名学生?原计划每名学生做多少面彩旗?
(1)、求安装健身器材的区域面积;(2)、当 , 时,求安装健身器材的区域面积.23. 某校为迎接市中学生田径运动会需准备240面彩旗.计划由八年级一班的3个小组完成此任务,3个小组的人数相等.后因1个小组另有任务,剩余2个小组的每名学生要比原计划多做4面彩旗才能完成任务,那么每个小组有多少名学生?原计划每名学生做多少面彩旗?冰冰:;
庆庆: .
根据以上信息,解答下列问题
(1)、冰冰同学所列方程中的表示 . 庆庆同学所列方程中的表示;(2)、请你选择其中一个方程解决提出的问题.24. 数学活动课上,张老师用如图1中的1张边长为a的正方形纸片A、1张边长为b的正方形纸片B和2张宽和长分别为a、b的长方形纸片C拼成了如图2所示的大正方形,观察图形并解答下列问题.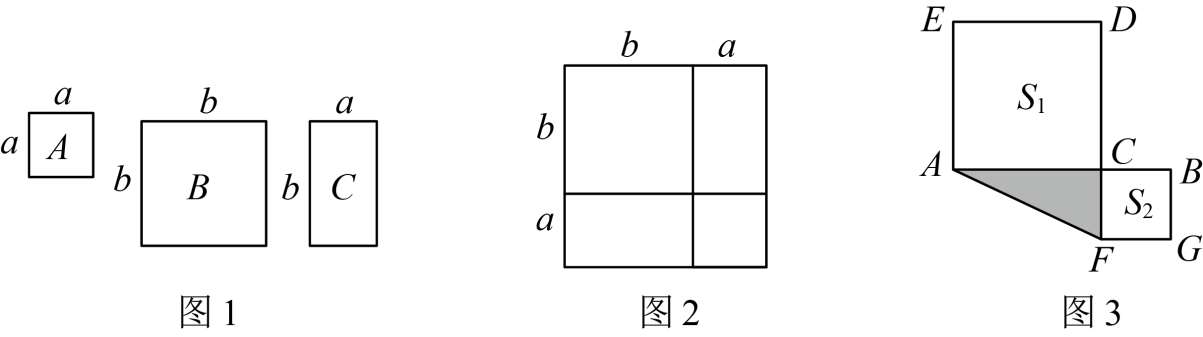 (1)、由图1和图2可以得到的等式为 . (用含a , b的式子表示)(2)、想用这三张纸片拼出一个面积为的大正方形,需要A , B , C三种纸片各多少张?(3)、如图3,已知点C为线段上的动点,分别以为边在的两侧作正方形和正方形 . 若 , 且两正方形的面积之和 , 求图中阴影部分的面积.25. 在中, , , 是的角平分线,于点E , 连接 .
(1)、由图1和图2可以得到的等式为 . (用含a , b的式子表示)(2)、想用这三张纸片拼出一个面积为的大正方形,需要A , B , C三种纸片各多少张?(3)、如图3,已知点C为线段上的动点,分别以为边在的两侧作正方形和正方形 . 若 , 且两正方形的面积之和 , 求图中阴影部分的面积.25. 在中, , , 是的角平分线,于点E , 连接 .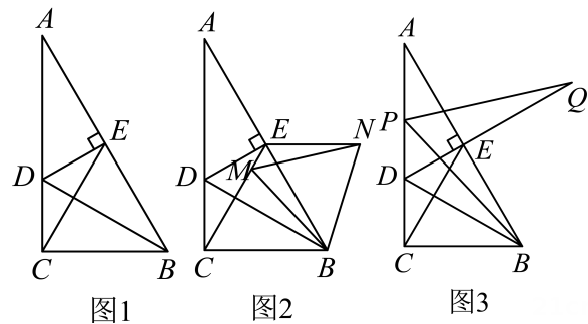 (1)、如图1,求证:是等边三角形;(2)、如图2,M为线段上一点,连接 , 作等边三角形 , 连接 , 求证:;(3)、如图3,P为线段上一点,连接 , 作 , 交的延长线于点Q , 探究线段 , 与之间的数量关系,并证明.
(1)、如图1,求证:是等边三角形;(2)、如图2,M为线段上一点,连接 , 作等边三角形 , 连接 , 求证:;(3)、如图3,P为线段上一点,连接 , 作 , 交的延长线于点Q , 探究线段 , 与之间的数量关系,并证明.