贵州省毕节市织金县2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-03-21 类型:期末考试
一、选择题(以下每题有A、B、C、D四个选项,只有一个选项正确,请将正确的选项填写在答题卷相应的位置上,每小题3分,共36分)
-
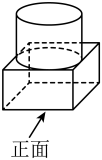
1. 由圆柱和长方体(底面为正方形)组成的几何体如图放置,该几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 下列方程中是关于x的一元二次方程的是( )A、 B、 C、 D、3. 如图,已知菱形的周长为 , , 则对角线的长是( )
2. 下列方程中是关于x的一元二次方程的是( )A、 B、 C、 D、3. 如图,已知菱形的周长为 , , 则对角线的长是( )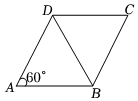 A、 B、 C、 D、4. 已知平行四边形ABCD中,对角线AC、BD相交于 . 则下列说法正确的是( )A、当时,平行四边形ABCD为矩形 B、当时,平行四边形ABCD为正方形 C、当时,平行四边形ABCD为菱形 D、当时,平行四边形ABCD为菱形5. 如图四边形四边形 , , , , 则( )
A、 B、 C、 D、4. 已知平行四边形ABCD中,对角线AC、BD相交于 . 则下列说法正确的是( )A、当时,平行四边形ABCD为矩形 B、当时,平行四边形ABCD为正方形 C、当时,平行四边形ABCD为菱形 D、当时,平行四边形ABCD为菱形5. 如图四边形四边形 , , , , 则( ) A、4 B、5 C、8 D、106. 将分别标有“大”、“美”、“织”、“金”汉字的四个小球装在一个不透明的口袋中,这些球除汉字外无其他差别,每次摸球前先搅拌均匀.随机摸出一球,不放回;再随机摸出一球.两次摸出的球上的汉字能组成“织金”的概率是( )A、 B、 C、 D、7. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的五个点A , B , C , D , E都在横线上,若线段 , 则线段CD的长是( )
A、4 B、5 C、8 D、106. 将分别标有“大”、“美”、“织”、“金”汉字的四个小球装在一个不透明的口袋中,这些球除汉字外无其他差别,每次摸球前先搅拌均匀.随机摸出一球,不放回;再随机摸出一球.两次摸出的球上的汉字能组成“织金”的概率是( )A、 B、 C、 D、7. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的五个点A , B , C , D , E都在横线上,若线段 , 则线段CD的长是( ) A、 B、2 C、 D、18. 如图,边长为2的正方形ABCD的中心与坐标原点重合,轴,将正方形ABCD绕原点顺时针旋2023次,每次旋转 , 则顶点的坐标是( )
A、 B、2 C、 D、18. 如图,边长为2的正方形ABCD的中心与坐标原点重合,轴,将正方形ABCD绕原点顺时针旋2023次,每次旋转 , 则顶点的坐标是( ) A、 B、 C、 D、9. 图形中,每个小网格均为正方形网格,带阴影部分的三角形中与如图相似的是( )
A、 B、 C、 D、9. 图形中,每个小网格均为正方形网格,带阴影部分的三角形中与如图相似的是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 若关于x的方程有实数根,则a的取值范围是( )A、且 B、 C、且 D、11. 如图,Rt△ABC中,∠C=90°,D是AC边上一点,AB=5,AC=4,若△ABC∽△BDC,则CD=( )
10. 若关于x的方程有实数根,则a的取值范围是( )A、且 B、 C、且 D、11. 如图,Rt△ABC中,∠C=90°,D是AC边上一点,AB=5,AC=4,若△ABC∽△BDC,则CD=( ) A、2 B、 C、 D、12. 在同一直角坐标系中,函数与的大致图象可能为( )A、
A、2 B、 C、 D、12. 在同一直角坐标系中,函数与的大致图象可能为( )A、 B、
B、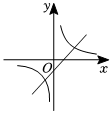 C、
C、 D、
D、
二、填空题(请将答案填写在答题卷相应的位置上,每小题4分,共16分)
-
13. 如图,乐器上的一根弦 , 两个端点A , B固定在乐器板面上,支撑点是靠近点的黄金分割点,支撑点是靠近点A的黄金分割点,C , D之间的距离为 .
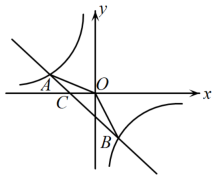
 14. 如图,点在双曲线的图象上,轴,垂足为 , 若 , 则该反比例函数的表达式为 .
14. 如图,点在双曲线的图象上,轴,垂足为 , 若 , 则该反比例函数的表达式为 . 15. 如图,在矩形ABCD中,对角线AC与BD相交于点O , AE垂直且平分线段BO , 垂足为点E , , 则AB的长为 .
15. 如图,在矩形ABCD中,对角线AC与BD相交于点O , AE垂直且平分线段BO , 垂足为点E , , 则AB的长为 . 16. 已知: , 是关于的方程的两个实数根 , 则的值为 .
16. 已知: , 是关于的方程的两个实数根 , 则的值为 .三、解答及证明(请将必要的文字说明、图形及必要的演算步骤或推理过程填写到答题卷相应题号的空格内,本题共9个小题,共98分)
-
17. 计算18. 先化简,再求值: , 其中满足 .19. 在平面直角坐标系中的位置如图所示:
 (1)、在网格内画出和以点为位似中心的位似图形 , 且和的位似比为2:1.(2)、分别写出、、三个点的坐标:
(1)、在网格内画出和以点为位似中心的位似图形 , 且和的位似比为2:1.(2)、分别写出、、三个点的坐标:, , .
(3)、求的面积.20. 织金县某学校为落实“双减”工作,增强课后服务的吸引力,充分用好课后服务时间,为学有余力的学生拓展学习空间,成立了5个活动小组(每位学生只能参加一个活动小组):A . 足球;B . 篮球;C . 摄影;D . 舞蹈;E . 主持人.为了解学生对以上活动的参与情况,随机抽取部分学生进行了调查统计,并根据统计结果,绘制了如图所示的两幅不完整的统计图.
根据图中信息,解答下列问题:
(1)、①此次调查一共随机抽取了_▲_名学生;②补全条形统计图(要求在条形图上方注明人数);
③扇形统计图中圆心角_▲_度;
(2)、若该校有2400名学生,估计该校参加D组(舞蹈)的学生人数;(3)、学校计划从E组(主持人)的甲、乙、丙、丁四位学生中随机抽取两人参加毕节市青少年“小小主持人”竞赛,请用树状图法或列表法求出恰好抽中甲、乙两人的概率.21. 如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.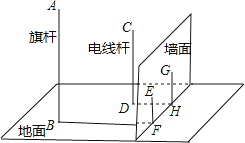 (1)、该小组的同学在这里利用的是 投影的有关知识进行计算的;(2)、试计算出电线杆的高度,并写出计算的过程。
(1)、该小组的同学在这里利用的是 投影的有关知识进行计算的;(2)、试计算出电线杆的高度,并写出计算的过程。
22. 如图,同一平面内三条不同的直线AB , CD , MN , , 直线MN与另外两条直线分别交于点M , N , 点E , F分别为AB , CD上两点,且满足MF平分. , NE平分 . (1)、求证:四边形ENFM为平行四边形;(2)、若四边形ENFM为菱形,求出的大小.23. 春节前夕,织金某超市从厂家分两次购进猪肉馅饺子和韭菜馅饺子,两次进货时,两种饺子的进价不变.第一次购进猪肉馅饺子60袋和韭菜馅饺子90袋,总费用为4800元;第二次购进猪肉馅饺子40袋和韭菜馅饺子80袋,总费用为3600元.(1)、求猪肉馅饺子、韭菜馅饺子每袋的进价各是多少元?(2)、当猪肉馅饺子销售价为每袋70元时;每天可售出20袋,为了促销,该超市决定对猪肉馅饺子进行降价销售.经市场调研,若每袋的销售价每降低1元,则每天的销售量将增加5袋.当猪肉馅饺子每袋的销售价为多少元时,每天售出猪肉馅饺子所获得的利润为220元?
(1)、求证:四边形ENFM为平行四边形;(2)、若四边形ENFM为菱形,求出的大小.23. 春节前夕,织金某超市从厂家分两次购进猪肉馅饺子和韭菜馅饺子,两次进货时,两种饺子的进价不变.第一次购进猪肉馅饺子60袋和韭菜馅饺子90袋,总费用为4800元;第二次购进猪肉馅饺子40袋和韭菜馅饺子80袋,总费用为3600元.(1)、求猪肉馅饺子、韭菜馅饺子每袋的进价各是多少元?(2)、当猪肉馅饺子销售价为每袋70元时;每天可售出20袋,为了促销,该超市决定对猪肉馅饺子进行降价销售.经市场调研,若每袋的销售价每降低1元,则每天的销售量将增加5袋.当猪肉馅饺子每袋的销售价为多少元时,每天售出猪肉馅饺子所获得的利润为220元?