贵州省黔南州2023-2024学年七年级上学期期末数学试卷
试卷更新日期:2024-03-21 类型:期末考试
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 的相反数是( )A、 B、 C、 D、2. 据中新网贵州新闻月日电,贵南高铁贵州段开通运营以来,荔波站共发送旅客人次,用科学记数法表示为( )A、 B、 C、 D、3. 如图是正方体的一种展开图,每个面上分别写有年杭州亚运会的办赛理念“绿色、智能、节俭”,那么与“绿”字相对的汉字是( )
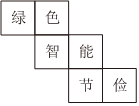 A、智
A、智
B、俭
C、节
D、能4. 单项式的系数和次数分别是( )A、 , B、 , C、 D、5. 已知点表示的数的绝对值为 , 则点可能在下列哪个位置( )A、 B、
B、 C、
C、 D、
D、 6. 下列计算正确的是( )A、 B、 C、 D、7. 下列方程变形错误的是( )A、由 , 得 B、由 , 得 C、由 , 得 D、由 , 得8. 如图,小明家到学校共有四条路,但小明基本上都选择了路线上学,他这么选择利用的数学依据是( )
6. 下列计算正确的是( )A、 B、 C、 D、7. 下列方程变形错误的是( )A、由 , 得 B、由 , 得 C、由 , 得 D、由 , 得8. 如图,小明家到学校共有四条路,但小明基本上都选择了路线上学,他这么选择利用的数学依据是( ) A、两点之间,线段最短 B、两点之间,直线最短
A、两点之间,线段最短 B、两点之间,直线最短
C、两点确定一条直线 D、两点之间,弧线最短9. 如图,将刻度尺放在数轴上,让和刻度线分别与数轴上表示和的两点重合对齐,则数轴上与刻度线对齐的点表示的数为( ) A、 B、 C、 D、10. 是下列哪个方程的解( )A、 B、 C、 D、11. 如图,射线的方向是北偏东 , 射线的方向是北偏西 , 已知射线平分 , 则射线的方向是( )
A、 B、 C、 D、10. 是下列哪个方程的解( )A、 B、 C、 D、11. 如图,射线的方向是北偏东 , 射线的方向是北偏西 , 已知射线平分 , 则射线的方向是( )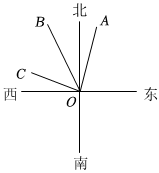 A、北偏西 B、西偏北 C、北偏西 D、西偏北12. 如图,是年月的月历,任意选取“十”字型中的五个数比如图中阴影部分 , 若移动“十”字型后所得五个数之和为 , 那么该“十”字型中正中间的号数为( )
A、北偏西 B、西偏北 C、北偏西 D、西偏北12. 如图,是年月的月历,任意选取“十”字型中的五个数比如图中阴影部分 , 若移动“十”字型后所得五个数之和为 , 那么该“十”字型中正中间的号数为( )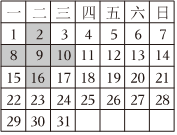 A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共4小题,每小题4分,共16分。
-
13. 的底数是 .14. 已知 , 则的余角等于 .15. 已知 , 则 .16. 如图,用圆形按如图所示的规律摆放图案,则第个图案摆放的圆形的个数为个

三、解答题:本题共7小题,共48分。解答应写出文字说明,证明过程或演算步骤。
-
17. 计算:
(1)、;(2)、 .18. 已知平面上的三个点、、和直线 , 根据要求画图.
画射线;
确定点的位置,使得点既在直线上,又在直线上;
在直线上确定点的位置,使得点到点与点的距离之和最小.19. 下面是小红解一元一次方程的主要过程,请仔细阅读小红的解题过程,
解决下列问题.
解:去分母,得
去括号,得
移项,得
合并同类项,得(1)、小红在以上解方程过程中,从第步开始出现错误,出现的错误是 .(2)、请写出正确的解答过程.20. 小伟是一个懂事的孩子,他每天都会从妈妈给的零花钱中存下一部分,他原计划每天存元,下表是小伟在某一周实际各天存钱的情况多存记为“”,不足记为“” .星期
星期一
星期二
星期三
星期四
星期五
星期六
星期日
存钱元
(1)、小伟在这一周中存钱最多的一天是星期 , 这一天存了元(2)、请计算小伟这一周存了多少钱?21. 如图所示,点是线段的中点, . (1)、若 , , 则 , ;(2)、若 , , 求线段的长用含、的式子表示 .22. 如图是学校手工艺社团编织的手工花朵,一朵花由个花心和个花瓣构成,已知手工艺社团有人,据统计,每个学生一节课可以编织个花心或个花瓣安排多少人编织花心,多少人编织花瓣,才能使一节课编织出来的花心和花瓣刚好配套?
(1)、若 , , 则 , ;(2)、若 , , 求线段的长用含、的式子表示 .22. 如图是学校手工艺社团编织的手工花朵,一朵花由个花心和个花瓣构成,已知手工艺社团有人,据统计,每个学生一节课可以编织个花心或个花瓣安排多少人编织花心,多少人编织花瓣,才能使一节课编织出来的花心和花瓣刚好配套? 23. 阅读材料
23. 阅读材料
材料:学习绝对值时,我们知道表示数的点与原点的距离,即 , 也可以说表示数轴上数与数对应的两点之间的距离,同理,数轴上数和数两点间的距离可以表示为或 .
例如数轴上表示和的两点间的距离为或 .
发现解题规律:
若 , 则或;
若 , 则或 , 得或;
若 , 则或 , 得或 .
结合上面的发现解决下列问题.(1)、数轴上表示和两点之间的距离是 .(2)、若 , 则 或 .(3)、如图所示,当点、所表示的数分别为和时,是否存在一点 , 使得点到、两点的距离之和等于?若存在,设点表示的数为 , 求的值;若不存在,请说明理由.