贵州省毕节市威宁彝族回族苗族自治县2023-2024学年八年级上学期期末数学试题
试卷更新日期:2024-03-21 类型:期末考试
一、选择题(每小题3分,共36分.每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B铅笔在答题卡相应位置填涂)
-
1. 2023的算术平方根是( )A、2023 B、 C、 D、2. 下列各组数,是勾股数的是( )A、1,2,3 B、0.3,0.4,0.5 C、 , , D、7,24,253. 一把直尺按如图所示摆放, , 且 , 则的度数是( )
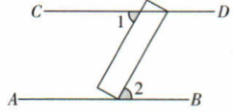 A、70° B、60° C、30° D、80°4. 在平面直角坐标系中,点的坐标是 , 则点到轴的距离是( )A、3 B、4 C、5 D、25. 若是方程的一个解,则的值是( )A、 B、 C、3 D、6. 2023年9月5日是第八个“中华慈善日”,主题为“携手参与慈善,共创美好生活”.某校为了响应中华慈善总会的号召,举行捐款活动.下表是某班的捐款金额统计情况,则该班捐款金额的众数和中位数分别是( )
A、70° B、60° C、30° D、80°4. 在平面直角坐标系中,点的坐标是 , 则点到轴的距离是( )A、3 B、4 C、5 D、25. 若是方程的一个解,则的值是( )A、 B、 C、3 D、6. 2023年9月5日是第八个“中华慈善日”,主题为“携手参与慈善,共创美好生活”.某校为了响应中华慈善总会的号召,举行捐款活动.下表是某班的捐款金额统计情况,则该班捐款金额的众数和中位数分别是( )捐款金额/元 1 2 3 5 10 人数 5 8 9 15 8 A、5,3 B、15,3 C、15,5 D、5,57. 下列语句中是命题的是( )A、作的平分线 B、美丽的大自然 C、同位角相等 D、你吃饭了吗8. 一次函数的图象经过的象限是( )A、第一、三、四象限 B、第一、二、三象限 C、第一、二、四象限 D、第二、三、四象限9. 估算的取值范围在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间10. 我国古代数学著作《九章算术》中有一道阐述“盈不足术”的问题,译文为:现有几个人共同购买一个物品,每人出8元,则多3元;每人出7元,则差4元.问这个物品的价格是多少元?有多少人共同购买?设这个物品的价格是元,有人共同购买,则可列出的方程组为( )A、 B、 C、 D、11. 如图,一次函数的图象过点 , 则当时,的取值范围是( ) A、 B、 C、 D、12. 如图,在平面直角坐标系中, , , , …都是斜边在轴上的等腰直角三角形,点 , , , …,则根据图示规律,点的坐标为( )
A、 B、 C、 D、12. 如图,在平面直角坐标系中, , , , …都是斜边在轴上的等腰直角三角形,点 , , , …,则根据图示规律,点的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题4分,共16分)
-
13. 若二次根式在实数范围内有意义,则的取值范围是.14. 在平面直角坐标系中,点关于轴的对称点的坐标为.15. 如图,直线与直线相交于点 , 则关于 , 的方程组的解是.
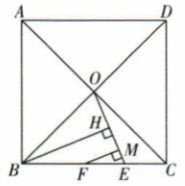
 16. 如图,四边形是等腰梯形,上底 , 过点作 , 且 , 连接.若的面积为 , 则的长为cm.
16. 如图,四边形是等腰梯形,上底 , 过点作 , 且 , 连接.若的面积为 , 则的长为cm.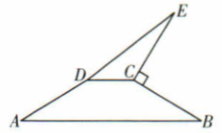
三、解答题(本大题共9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤)
-
17.(1)、计算:;(2)、解方程组:18. 如图,在平面直角坐标系中,各顶点的坐标分别为 , , .
 (1)、在图中作 , 使和关于轴对称;(2)、分别写出点 , , 的坐标;(3)、求的面积.19. 我县某校为了落实“五育并举”,促进学生全面发展,决定开设以下的社团活动:A.人工智能;B.舞蹈;C.美术;D.篮球;E.音乐;F.足球.为了了解学生最喜欢哪一个活动,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图.请回答下列问题:
(1)、在图中作 , 使和关于轴对称;(2)、分别写出点 , , 的坐标;(3)、求的面积.19. 我县某校为了落实“五育并举”,促进学生全面发展,决定开设以下的社团活动:A.人工智能;B.舞蹈;C.美术;D.篮球;E.音乐;F.足球.为了了解学生最喜欢哪一个活动,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图.请回答下列问题: (1)、这次被调查的学生共有多少人?(2)、请你将条形统计图补充完整,并求出D活动对应的扇形圆心角的度数.(3)、假如该校共有2600人,估计参加人工智能活动的有多少人.20. 如图是一块四边形绿地的示意图,其中 , 米,米,米,米,求绿地的面积.
(1)、这次被调查的学生共有多少人?(2)、请你将条形统计图补充完整,并求出D活动对应的扇形圆心角的度数.(3)、假如该校共有2600人,估计参加人工智能活动的有多少人.20. 如图是一块四边形绿地的示意图,其中 , 米,米,米,米,求绿地的面积.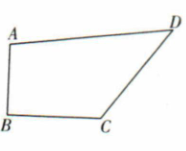 21. 已知的立方根是2,的算术平方根是3.(1)、求 , 的值;(2)、求的平方根.22. 某中学为了在11月中旬举办体育文化节,学校委托后勤处张主任去购买奖品,张主任回校后向财务处的陈老师交账说:“我买了足球和篮球共20个,足球每个60元,篮球每个80元,去买之前我领了1500元,现在还余70元.”陈老师算了一下,说:“你肯定搞错了.”(1)、陈老师为什么说张主任肯定搞错了?试用方程的知识给予解释.(2)、张主任连忙拿出购物发票,发现的确弄错了,因为他还买了几个(大于1小于4)单价为15元的水龙头,但是发票上的个数看不清了,请你帮他算一算,他买了几个水龙头?23. 一天下午,某网约车师傅开车从威宁到贵阳,汽车出发前油箱中有25升油,行驶一段时间后,师傅感觉有点疲倦,于是就到服务区休息了一会儿.当师傅打算继续上路向贵阳方向行驶时,发现油箱中的油不多了,于是就在该服务区的加油站加了油(加油时间忽略不计),才继续上路行驶.已知进入服务区前和驶出服务区后汽车都匀速行驶,汽车行驶时每小时的耗油量一定.油箱中剩余油量(升)与汽车的行驶时间(时)之间的函数图象如图所示.
21. 已知的立方根是2,的算术平方根是3.(1)、求 , 的值;(2)、求的平方根.22. 某中学为了在11月中旬举办体育文化节,学校委托后勤处张主任去购买奖品,张主任回校后向财务处的陈老师交账说:“我买了足球和篮球共20个,足球每个60元,篮球每个80元,去买之前我领了1500元,现在还余70元.”陈老师算了一下,说:“你肯定搞错了.”(1)、陈老师为什么说张主任肯定搞错了?试用方程的知识给予解释.(2)、张主任连忙拿出购物发票,发现的确弄错了,因为他还买了几个(大于1小于4)单价为15元的水龙头,但是发票上的个数看不清了,请你帮他算一算,他买了几个水龙头?23. 一天下午,某网约车师傅开车从威宁到贵阳,汽车出发前油箱中有25升油,行驶一段时间后,师傅感觉有点疲倦,于是就到服务区休息了一会儿.当师傅打算继续上路向贵阳方向行驶时,发现油箱中的油不多了,于是就在该服务区的加油站加了油(加油时间忽略不计),才继续上路行驶.已知进入服务区前和驶出服务区后汽车都匀速行驶,汽车行驶时每小时的耗油量一定.油箱中剩余油量(升)与汽车的行驶时间(时)之间的函数图象如图所示. (1)、师傅开车行驶小时后去服务区休息,此时用了升油.(2)、求进入服务区前的与之间的函数关系式.(3)、加完油时,刚好是下午4:40,此时距贵阳还有136千米,若汽车行驶的速度为85千米/时,师傅能在下午6:10前赶到贵阳吗?(4)、若该师傅到达贵阳后,接到客人又马上返回威宁,请问他不加油行吗?
(1)、师傅开车行驶小时后去服务区休息,此时用了升油.(2)、求进入服务区前的与之间的函数关系式.(3)、加完油时,刚好是下午4:40,此时距贵阳还有136千米,若汽车行驶的速度为85千米/时,师傅能在下午6:10前赶到贵阳吗?(4)、若该师傅到达贵阳后,接到客人又马上返回威宁,请问他不加油行吗?