贵州省六盘水市盘州市2023-2024学年七年级上学期期末数学试题
试卷更新日期:2024-03-21 类型:期末考试
一、选择题(每小题3分,共36分)
-
1. 下列学习或生活中的物品,它的形状可以近似地看作圆柱体的是( )A、
 B、
B、 C、
C、 D、
D、 2. 小明步行上学,速度为米/秒,小亮乘车上学,速度是小明的5倍,则小亮乘车的速度可表示为( )A、米/秒 B、米/秒 C、米/秒 D、米/秒3. 平板电脑支架方便用户在不同位置和角度观看平板电脑,如图是支架侧面的平画示意图,其中还可以表示为( )
2. 小明步行上学,速度为米/秒,小亮乘车上学,速度是小明的5倍,则小亮乘车的速度可表示为( )A、米/秒 B、米/秒 C、米/秒 D、米/秒3. 平板电脑支架方便用户在不同位置和角度观看平板电脑,如图是支架侧面的平画示意图,其中还可以表示为( ) A、 B、 C、 D、4. 如图,整数在数轴上所对应的点的位置被“
A、 B、 C、 D、4. 如图,整数在数轴上所对应的点的位置被“ ”盖住了,则表示的整数是( )
”盖住了,则表示的整数是( ) A、-1 B、-2 C、-3 D、-45. 将一个正方体的表面沿某些棱剪开,不能展开成下列哪个平面图形( )A、
A、-1 B、-2 C、-3 D、-45. 将一个正方体的表面沿某些棱剪开,不能展开成下列哪个平面图形( )A、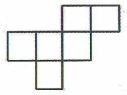 B、
B、 C、
C、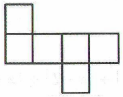 D、
D、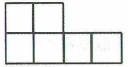 6. 每年的6月6日是全国爱眼日,2023年爱眼日的主题是“关注普遍的眼睛健康”.某中学七年级数学活动兴趣小组为了解该校2000名学生的视力情况,制定了如下调查方案,最合理的方案是( )A、按学籍号随机抽取200名学生进行调查 B、按学籍号随机抽取5名学生进行调查 C、抽取本校九年级全体学生进行调查 D、抽取八年级100名女生进行调查7. 过某多边形一个顶点的所有对角线,将这个多边形分成4个三角形,则这个多边形是( )A、四边形 B、五边形 C、六边形 D、七边形8. 从正方形的纸片上,剪去3cm宽的一个长方形条,余下的面积为 , 设原正方形纸片的边长为 , 根据题意可以列得方程( )A、 B、 C、 D、9. 已知线段 , 延长至点 , 使 , 点 , 分别为线段 , 的中点,则的长度为( )A、2cm B、3cm C、5cm D、1cm或5cm10. 已知单项式与单项式相加的结果还是一个单项式,则下列说法一定正确的是( )A、的值为2,的值为3 B、的值为2,的值为3 C、的值为2,的值为3 D、的值为3,的值为211. 有理数 , 在数轴上对应的点的位置如图所示,则关于与的运算结果叙述正确的是( )
6. 每年的6月6日是全国爱眼日,2023年爱眼日的主题是“关注普遍的眼睛健康”.某中学七年级数学活动兴趣小组为了解该校2000名学生的视力情况,制定了如下调查方案,最合理的方案是( )A、按学籍号随机抽取200名学生进行调查 B、按学籍号随机抽取5名学生进行调查 C、抽取本校九年级全体学生进行调查 D、抽取八年级100名女生进行调查7. 过某多边形一个顶点的所有对角线,将这个多边形分成4个三角形,则这个多边形是( )A、四边形 B、五边形 C、六边形 D、七边形8. 从正方形的纸片上,剪去3cm宽的一个长方形条,余下的面积为 , 设原正方形纸片的边长为 , 根据题意可以列得方程( )A、 B、 C、 D、9. 已知线段 , 延长至点 , 使 , 点 , 分别为线段 , 的中点,则的长度为( )A、2cm B、3cm C、5cm D、1cm或5cm10. 已知单项式与单项式相加的结果还是一个单项式,则下列说法一定正确的是( )A、的值为2,的值为3 B、的值为2,的值为3 C、的值为2,的值为3 D、的值为3,的值为211. 有理数 , 在数轴上对应的点的位置如图所示,则关于与的运算结果叙述正确的是( ) A、的结果为正数 B、的结果为正数 C、的结果为正数 D、的结果为正数12. 如图,将面积为1的长方形纸片分割成8个部分,部分①的面积是原长方形纸片面积的一半,部分②的面积是部分①面积的一半,部分③的面积是部分②面积的一半,依次类推,阴影部分的面积为( )
A、的结果为正数 B、的结果为正数 C、的结果为正数 D、的结果为正数12. 如图,将面积为1的长方形纸片分割成8个部分,部分①的面积是原长方形纸片面积的一半,部分②的面积是部分①面积的一半,部分③的面积是部分②面积的一半,依次类推,阴影部分的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题4分,共16分)
-
13. 整数-2024的相反数是.14. “世界桥梁看中国,中国桥梁看贵州”.下图是贵州一座横跨峡谷的大桥,天堑变通途,径直的大桥极大程度地缩短了大桥两端的路程,其中“径直的大桥缩短了大桥两端的路程”所蕴含的数学原理是.
 15. 全球每年大约有577000000000000立方米的水从海洋和陆地转化为大气中的水汽,将577000000000000这个数据用科学记数法表示为 , 则的值是.16. 如图1是我国南宋数学家杨辉所著的《详解九章算法》一书中出现的“杨辉三角”,“杨辉三角”中的数字排列有一定的规律.如图2,从第三行起,把每一行的第三个数字依次用 , , …来表示,即 , , …则.
15. 全球每年大约有577000000000000立方米的水从海洋和陆地转化为大气中的水汽,将577000000000000这个数据用科学记数法表示为 , 则的值是.16. 如图1是我国南宋数学家杨辉所著的《详解九章算法》一书中出现的“杨辉三角”,“杨辉三角”中的数字排列有一定的规律.如图2,从第三行起,把每一行的第三个数字依次用 , , …来表示,即 , , …则.
图1 图2
三、解答题(本大题共9题,共计98分,解答应写出必要的文字说明或演算步骤)
-
17. 计算:(1)、;(2)、.18. 一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置小立方块的个数,依次完成下列问题.
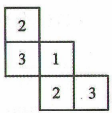 (1)、请画出从正面和左面看到的这个几何体的形状图;
(1)、请画出从正面和左面看到的这个几何体的形状图;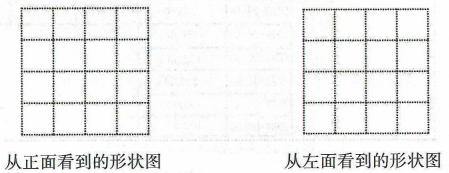 (2)、继续添加相同的小立方块与原几何体搭成一个新的几何体,使新几何体从正面、左面看到的形状图与原几何体从正面、左面看到的形状图相同,则最多可以添加个.19. “学习生活两不误,劳逸结合更健康”,某个周末勤奋好学的小明和爸爸下棋,爸爸赢一盘记2分,小明赢一盘记6分,一共下了8盘,每盘都分出了胜负.(1)、若两人得分相等,请应用方程求出两人各赢了多少盘;(2)、比赛结束时,爸爸得分可能比小明得分多2分吗?为什么?20. 如图,点在直线上,射线将分成了 , 两个角, , 分别平分 , .
(2)、继续添加相同的小立方块与原几何体搭成一个新的几何体,使新几何体从正面、左面看到的形状图与原几何体从正面、左面看到的形状图相同,则最多可以添加个.19. “学习生活两不误,劳逸结合更健康”,某个周末勤奋好学的小明和爸爸下棋,爸爸赢一盘记2分,小明赢一盘记6分,一共下了8盘,每盘都分出了胜负.(1)、若两人得分相等,请应用方程求出两人各赢了多少盘;(2)、比赛结束时,爸爸得分可能比小明得分多2分吗?为什么?20. 如图,点在直线上,射线将分成了 , 两个角, , 分别平分 , . (1)、若 , 求的度数;(2)、若 , 求的度数.21. 如图,一页账单有一部分破损了,该账单记录了2023年5月26日至2023年9月6日支出数、存入数及结余数情况,存入记为正,支出记为负,请根据账单中的信息完成下列问题.
(1)、若 , 求的度数;(2)、若 , 求的度数.21. 如图,一页账单有一部分破损了,该账单记录了2023年5月26日至2023年9月6日支出数、存入数及结余数情况,存入记为正,支出记为负,请根据账单中的信息完成下列问题. (1)、该页账单中9月6日的结余数与5月26日的结余数相比,是变多还是变少了?为什么;(2)、请根据该页账单中的残余数字计算8月12日的结余数.22. 已知 , .(1)、求;(2)、若关于的方程 , , 求方程的解,并计算的值.23. 国家卫健委公布的数据显示截止到2021年年底,我国60岁及以上的老年人口数量达到了2.67亿,小明为了了解七年级(1)班同学各自家庭中老年人口数量情况,对七年级(1)班全体同学各自家庭中老年人口数量进行了调查,根据调查的结果制作了两幅不完整统计图,请根据统计图中的信息完成下列问题.
(1)、该页账单中9月6日的结余数与5月26日的结余数相比,是变多还是变少了?为什么;(2)、请根据该页账单中的残余数字计算8月12日的结余数.22. 已知 , .(1)、求;(2)、若关于的方程 , , 求方程的解,并计算的值.23. 国家卫健委公布的数据显示截止到2021年年底,我国60岁及以上的老年人口数量达到了2.67亿,小明为了了解七年级(1)班同学各自家庭中老年人口数量情况,对七年级(1)班全体同学各自家庭中老年人口数量进行了调查,根据调查的结果制作了两幅不完整统计图,请根据统计图中的信息完成下列问题. (1)、求七年级(1)班的学生人数;(2)、请补全条形统计图;(3)、计算扇形统计图中部分所对的圆心角的度数.24. 如图,在直角三角形中, , , , 若点从点开始沿边向点以2厘米每秒的速度移动,同时点从点开始沿边向点以4厘米每秒的速度移动,当有一点到达终点时,另一点也随之停止移动.
(1)、求七年级(1)班的学生人数;(2)、请补全条形统计图;(3)、计算扇形统计图中部分所对的圆心角的度数.24. 如图,在直角三角形中, , , , 若点从点开始沿边向点以2厘米每秒的速度移动,同时点从点开始沿边向点以4厘米每秒的速度移动,当有一点到达终点时,另一点也随之停止移动. (1)、设 , 两点移动的时间为秒,则线段的长度为cm,线段的长度为cm;(2)、当点移动到线段的中点时,求线段的长度;(3)、在 , 两点移动过程中,是否存在某一时刻,使得 , 若存在,请求出 , 的移动时间,总不存在,请说明理由.25.(1)、【阅读理解】
(1)、设 , 两点移动的时间为秒,则线段的长度为cm,线段的长度为cm;(2)、当点移动到线段的中点时,求线段的长度;(3)、在 , 两点移动过程中,是否存在某一时刻,使得 , 若存在,请求出 , 的移动时间,总不存在,请说明理由.25.(1)、【阅读理解】如图所示,或可以表示在同一条数轴上1所对应的点与3所对应的点之间的距离.

根据以上信息,在同一条数轴上有理数所对应的点与所对应的点之间的距离可表示为(只写一种).
(2)、【探索发现】若有理数 , , 5在同一条数轴上所对应的点分别为 , , , 求的值,当的值最小时,点在什么位置?
(3)、【联系拓广】直接写出的最小值.