贵州省六盘水市盘州市2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-03-21 类型:期末考试
一、选择题(每小题3分,共36分,每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B铅笔在答题卡相应位置填涂)
-
1. 下列几何体的三种视图完全相同的是( )A、
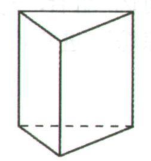 B、
B、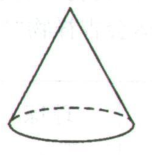 C、
C、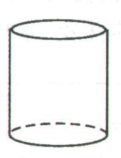 D、
D、 2. 下列图形中,对称轴最多的是( )A、
2. 下列图形中,对称轴最多的是( )A、 B、
B、 C、
C、 D、
D、 3. 在一间黑屋子里用一盏白炽灯照如图所示的球,球在地面上的影子是圆形,当把球竖直向上靠近白炽灯时,影子的大小会怎样变化( )
3. 在一间黑屋子里用一盏白炽灯照如图所示的球,球在地面上的影子是圆形,当把球竖直向上靠近白炽灯时,影子的大小会怎样变化( )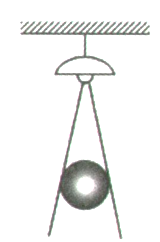 A、越来越小 B、越来越大 C、大小不变 D、不能确定4. 如图,要使成为菱形,则需添加的一个条件是( )
A、越来越小 B、越来越大 C、大小不变 D、不能确定4. 如图,要使成为菱形,则需添加的一个条件是( ) A、 B、 C、 D、5. 已知点都在反比例函数的图象上,且 , 则有( )A、 B、 C、 D、6. 如图,在中,点分别是的中点,连接 , 则( )
A、 B、 C、 D、5. 已知点都在反比例函数的图象上,且 , 则有( )A、 B、 C、 D、6. 如图,在中,点分别是的中点,连接 , 则( ) A、 B、 C、 D、7. 两千多年前,古希腊数学家欧多克索斯发现了黄金分割,黄金分割在日常生活中随处可见.例如:主持人在舞台上主持节目时,站在黄金分割点上,观众看上去感觉最好.若舞台长10米,主持人从舞台一侧进人,设他至少走米时恰好站在舞台的黄金分割点上主持节目,则满足的方程是( )A、 B、 C、 D、8. 某数学兴趣小组做“用频率估计概率”的试验时,统计了某结果出现的频率,绘制了如下的表格,则符合这一结果的试验最有可能是
A、 B、 C、 D、7. 两千多年前,古希腊数学家欧多克索斯发现了黄金分割,黄金分割在日常生活中随处可见.例如:主持人在舞台上主持节目时,站在黄金分割点上,观众看上去感觉最好.若舞台长10米,主持人从舞台一侧进人,设他至少走米时恰好站在舞台的黄金分割点上主持节目,则满足的方程是( )A、 B、 C、 D、8. 某数学兴趣小组做“用频率估计概率”的试验时,统计了某结果出现的频率,绘制了如下的表格,则符合这一结果的试验最有可能是试验总次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333
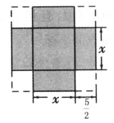
A、掷一枚质地均匀的硬币,出现反面朝上 B、掷一枚质地均匀的骰子,掷得朝上的点数是5 C、在“石头、剪刀、布”游戏中,小明出的是“剪刀” D、将一副去掉大小王的普通扑克牌洗匀后,从中任抽一张扑克牌的花色是红桃9. 彭老师身高 , 在某一时刻测得她站在阳光下的影子长为 , 紧接着她把手臂竖直举起,测得影子长为 , 那么彭老师举起的手臂超出头顶的长度为( )A、 B、 C、 D、10. 若是一元二次方程的两个实数根,则的值为( )A、 B、3 C、5 D、711. 如图,矩形的顶点在轴上,反比例函数的图象经过边的中点和点 , 若 , 则的值为( ) A、5 B、6 C、7 D、812. 清初曾传入中国两卷无作者的代数学书,被译为《阿尔热巴拉新法》,后由中国近代数学家李善兰改译为《代数学》.该书中记载,形如的方程,求正数解的几何方法是:“如图①,先构造一个面积为的正方形,再以该正方形的边长为一边向外构造四个面积均为的矩形,则大正方形的面积为 , 则原方程的正数解为".小聪按此方法解关于的方程时,构造出如图②所示的图形,已知阴影部分的面积为156,则该方程的正数解为( )
A、5 B、6 C、7 D、812. 清初曾传入中国两卷无作者的代数学书,被译为《阿尔热巴拉新法》,后由中国近代数学家李善兰改译为《代数学》.该书中记载,形如的方程,求正数解的几何方法是:“如图①,先构造一个面积为的正方形,再以该正方形的边长为一边向外构造四个面积均为的矩形,则大正方形的面积为 , 则原方程的正数解为".小聪按此方法解关于的方程时,构造出如图②所示的图形,已知阴影部分的面积为156,则该方程的正数解为( )图①
 图②
图② A、6 B、8 C、16 D、
A、6 B、8 C、16 D、二、填空题(每小题4分,共16分)
-
13. 若 , 则 .14. 若是方程的一个根,则的值为 .15. 如图,一次函数的图象与反比例函数的图象相交于点和点 , 则关于的不等式的解集是 .
 16. 如图,正方形的边长为8,点为边上一点,且 , 点为边上的一个动点,连接 , 以为一条直角边向右侧作等腰 , 且使 , 连接 , 则的最小值是 .
16. 如图,正方形的边长为8,点为边上一点,且 , 点为边上的一个动点,连接 , 以为一条直角边向右侧作等腰 , 且使 , 连接 , 则的最小值是 .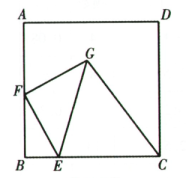
三、解答题(本大题共9题,共98分,解答应写出必要的文字说明、证明过程或演算步骤)
-
17. 解方程:(1)、;(2)、 .18. 在如图所示的平面直角坐标系中,每个小正方形的边长均为1,已知点 , 点 , 点 .
 (1)、画出;(2)、画出关于轴对称的;(3)、请以原点为位似中心在第一象限内画出 , 使它与位似,且相似比是 , 并写出三个顶点的坐标.19. “绿电”即绿色电力,是指在其生产过程中,二氧化碳排放量为零或趋近于零,相较于火力发电,对环境冲击影响较低的电力.绿电的主要来源为太阳能、风力、生物质能、地热等.为了解风力发电机每转动一圈的发电量(记为),现对不同功率的风力发电机每转动一圈的发电量进行了随机调查,调查结果全部收回后进行整理,绘制成如下不完整的频数分布表和频数分布直方图:
(1)、画出;(2)、画出关于轴对称的;(3)、请以原点为位似中心在第一象限内画出 , 使它与位似,且相似比是 , 并写出三个顶点的坐标.19. “绿电”即绿色电力,是指在其生产过程中,二氧化碳排放量为零或趋近于零,相较于火力发电,对环境冲击影响较低的电力.绿电的主要来源为太阳能、风力、生物质能、地热等.为了解风力发电机每转动一圈的发电量(记为),现对不同功率的风力发电机每转动一圈的发电量进行了随机调查,调查结果全部收回后进行整理,绘制成如下不完整的频数分布表和频数分布直方图:每台风力发电机转动一圈发电量频数分布表
发电量千瓦时
频数
频率
4
0.08
8
0.36
14
6
0.12

请根据图表中提供的信息,解答下列问题:
(1)、填空:_▲_,并将频数分布直方图补充完整;(2)、在某次综合与实践活动中,九(1)班学生为了进一步学习绿电的相关知识,收集到太阳能路灯、太阳能光伏板、风力发电、氢能源汽车的图片各一张,将其制成为除内容外都相同的四张卡片,他们将这四张卡片背面朝上,洗匀后放在桌面上,从中随机抽取两张,请用画树状图或列表的方法,求出抽到的两张卡片正面的图片恰好是太阳能路灯和氢能源汽车的概率.20. 如图,是等边三角形,点分别在边上, . (1)、求证:;(2)、若 , 求的长.21. 配方法不仅可以解一元二次方程,还可以求最值.
(1)、求证:;(2)、若 , 求的长.21. 配方法不仅可以解一元二次方程,还可以求最值.例如:求代数式的最值.
解:
(分离常数项)
(提二次项系数)
当时,代数式取得最小值是3
运用以上方法,解答下列问题:
(1)、求代数式的最值;(2)、关于的方程 . 求证:无论取何值,方程总有两个不相等的实数根.22. 如图,将矩形纸片沿折叠,使点与点重合,折痕交于点 , 交于点 , 与对角线交于点 , 连接 . (1)、求证:;(2)、若 , 求的长.23. 如图,正比例函数的图象与反比例函数的图象相交于点和点 .
(1)、求证:;(2)、若 , 求的长.23. 如图,正比例函数的图象与反比例函数的图象相交于点和点 .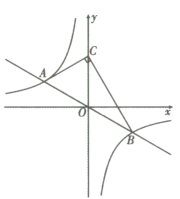 (1)、求反比例函数的表达式;(2)、若点在轴的正半轴上,且 , 求的面积;(3)、若点在轴上,且为锐角,直接写出的取值范围.24. 第19届亚洲运动会于2023年9月23日晚在浙江省杭州市隆重开幕.亚运会吉祥物是一组承载深厚底蕴和充满时代活力的机器人,由“踪琮”、“莲莲”、“宸宸”共同组成“江南忆”组合,三个吉祥物造型形象生动,深受大家的喜爱.某网店购进一批亚运会吉祥物“宸宸”和“琮琮”,进货价和销售价如下表:
(1)、求反比例函数的表达式;(2)、若点在轴的正半轴上,且 , 求的面积;(3)、若点在轴上,且为锐角,直接写出的取值范围.24. 第19届亚洲运动会于2023年9月23日晚在浙江省杭州市隆重开幕.亚运会吉祥物是一组承载深厚底蕴和充满时代活力的机器人,由“踪琮”、“莲莲”、“宸宸”共同组成“江南忆”组合,三个吉祥物造型形象生动,深受大家的喜爱.某网店购进一批亚运会吉祥物“宸宸”和“琮琮”,进货价和销售价如下表:吉祥物
价格
宸宸
琮琮
进货价(元/个)
59
66
销售价(元/个)
79
88
(1)、该网店第一次用3160元购进“宸宸”和“踪琮”共50个,求购进“宸宸”和“琮琮”各多少个;(2)、第一次购进的“宸宸”和“琮琮”售完后,该网店再次购进“宸宸”和“琮琮”共80个(进货价和销售价都不变),且进货总价不高于4900元,若进货后能全部售出,则应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少:(3)、亚运会临近结束时,该网店打算把“宸宸”调价销售,如果按照原价销售,平均每天可售8个,经调查发现,每降价1元,平均每天可多售2个,将销售价定为每个多少元时,才能使“宸宸”平均每天销售利润为288元.25. 如图,在矩形中, , 以点为旋转中心,将矩形沿顺时针方向旋转,得到矩形 , 点的对应点分别是点 .图①
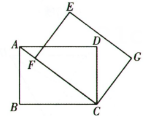 图②
图②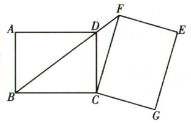 图③
图③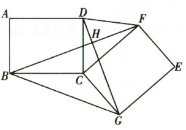 (1)、如图①,当点落在矩形的对角线上时,求线段的长;(2)、如图②,当点落在矩形的对角线的延长线上时,求的面积;(3)、如图③,将矩形旋转一定角度后,连接交于点 , 连接 , 直接写出的值.
(1)、如图①,当点落在矩形的对角线上时,求线段的长;(2)、如图②,当点落在矩形的对角线的延长线上时,求的面积;(3)、如图③,将矩形旋转一定角度后,连接交于点 , 连接 , 直接写出的值.