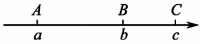贵州省六盘水市钟山区2023-2024学年七年级上学期期末数学试题
试卷更新日期:2024-03-21 类型:期末考试
一、选择题(每小题3分,共36分.每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B铅笔在答题卡相应位置作答)
-
1. 2024的相反数是( )A、 B、 C、 D、20242. 用一个平面去截下列几何体,截面一定是圆的是( )A、
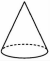 B、
B、 C、
C、 D、
D、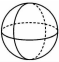 3. 中国是世界上最早认识和应用负数的国家,比西方早一千多年,在我国古代著名的数学专著《九章算术》中,首次引入负数.如果节约水记作 , 那么浪费水记作( )A、 B、 C、 D、4. 第八届中国凉都·六盘水夏季马拉松暨全国马拉松锦标赛(第二站)于2023年7月16日在六盘水市钟山区举行.本届马拉松赛事规模均为30000人,将数30000用科学记数法表示为( )A、 B、 C、 D、5. 如图,是六盘水市凤凰东路的交通示意图.2023年12月30日,凤凰东路整式通车,缩短了市民东西向出行的路程.能用数学知识解释这一现象的依据是( )
3. 中国是世界上最早认识和应用负数的国家,比西方早一千多年,在我国古代著名的数学专著《九章算术》中,首次引入负数.如果节约水记作 , 那么浪费水记作( )A、 B、 C、 D、4. 第八届中国凉都·六盘水夏季马拉松暨全国马拉松锦标赛(第二站)于2023年7月16日在六盘水市钟山区举行.本届马拉松赛事规模均为30000人,将数30000用科学记数法表示为( )A、 B、 C、 D、5. 如图,是六盘水市凤凰东路的交通示意图.2023年12月30日,凤凰东路整式通车,缩短了市民东西向出行的路程.能用数学知识解释这一现象的依据是( ) A、两点确定一条直线 B、两点之间,线段最短 C、经过一点有无数条直线 D、两直线相交只有一个交点6. 在下列调查中,适宜采用全面调查的是( )A、大型客机起飞前对仪器设备的检查 B、调查央视“启航2024”跨年晚会的收视情况 C、了解全市人民对六盘水旅发大会的关注情况 D、调查水城河的水质情况7. 过某个多边形一个顶点的所有对角线,将这个多边形分成7个三角形,则这个多边形是( )A、七边形 B、八边形 C、九边形 D、十边形8. 如图,射线表示北偏东方向,若射线与垂直,则射线表示( )
A、两点确定一条直线 B、两点之间,线段最短 C、经过一点有无数条直线 D、两直线相交只有一个交点6. 在下列调查中,适宜采用全面调查的是( )A、大型客机起飞前对仪器设备的检查 B、调查央视“启航2024”跨年晚会的收视情况 C、了解全市人民对六盘水旅发大会的关注情况 D、调查水城河的水质情况7. 过某个多边形一个顶点的所有对角线,将这个多边形分成7个三角形,则这个多边形是( )A、七边形 B、八边形 C、九边形 D、十边形8. 如图,射线表示北偏东方向,若射线与垂直,则射线表示( )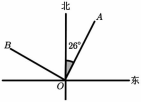 A、北偏西方向 B、北偏西方向 C、西北方向 D、北偏东方向9. 如果方程是关于的一元一次方程,那么的值是( )A、 B、0 C、 D、110. 下列说法中,正确的是( )A、的系数是 B、的次数是3 C、的常数项是2 D、与是同类项11. 三个有理数在数轴上表示的位置如图所示,则化简的结果是( )
A、北偏西方向 B、北偏西方向 C、西北方向 D、北偏东方向9. 如果方程是关于的一元一次方程,那么的值是( )A、 B、0 C、 D、110. 下列说法中,正确的是( )A、的系数是 B、的次数是3 C、的常数项是2 D、与是同类项11. 三个有理数在数轴上表示的位置如图所示,则化简的结果是( ) A、 B、 C、 D、012. 幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”.把洛书用今天的数学符号翻译出来,就是一个三阶幻方.将9个数填入三阶幻方的空格中,使得每行、每列、每条对角线上的三个数之和相等.如图是一个未完成的三阶幻方,则图中的值为( )
A、 B、 C、 D、012. 幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”.把洛书用今天的数学符号翻译出来,就是一个三阶幻方.将9个数填入三阶幻方的空格中,使得每行、每列、每条对角线上的三个数之和相等.如图是一个未完成的三阶幻方,则图中的值为( ) A、1 B、2 C、4 D、6
A、1 B、2 C、4 D、6二、填空题(每题4分,共16分)
-
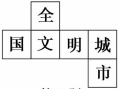
13. 比较大小:0(填“>”“<”或“=”).14. 如图是一个正方体的平面展开图,将其折叠成正方体后,与“城”字相对面上的汉字为 .
 15. “整体思想”是中学数学解题中一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.已知是方程的解,则的值为 .16. 如图,数轴上的点为原点,点表示的数为 , 动点从点出发,按以下规律跳动:第1次从点跳动到的中点处,第2次从点跳动到的中点处,第3次从点跳动到的中点处,…,第次从点跳动到的中点处,按照这样的规律继续跳动到点 , , , …,处,那么点所表示的数为 .
15. “整体思想”是中学数学解题中一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.已知是方程的解,则的值为 .16. 如图,数轴上的点为原点,点表示的数为 , 动点从点出发,按以下规律跳动:第1次从点跳动到的中点处,第2次从点跳动到的中点处,第3次从点跳动到的中点处,…,第次从点跳动到的中点处,按照这样的规律继续跳动到点 , , , …,处,那么点所表示的数为 .
三、解答题(本大题共8小题,共68分)
-
17.(1)、计算:(2)、解方程:18. 小龙同学在计算时,解答过程如下:
……第一步
……第二步
……第三步
(1)、小龙同学的解答从第步开始出错;(2)、请写出正确的解答过程.19. 观察如图所示的几何体,已知小正方体的棱长为1.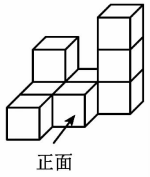 (1)、该几何体的体积为;(2)、请在下面网格中分别画出你从正面、左面、上面所看到的几何体的形状图.
(1)、该几何体的体积为;(2)、请在下面网格中分别画出你从正面、左面、上面所看到的几何体的形状图. 从正面看
从正面看  从左面看
从左面看  从上面看20. 2023年10月26日,神州十七号载人飞船在酒泉卫星发射中心成功发射.某中学科技兴趣小组为了解本校学生对航天科技的关注程度,将“关注程度”分为四类:A类为“非常关注”,B类为“比较关注”,C类为“关注”,D类为“不关注”.该小组在校内进行了随机调查,并将调查结果绘制成如下两幅统计图,请根据统计图中的信息解答下列问题:
从上面看20. 2023年10月26日,神州十七号载人飞船在酒泉卫星发射中心成功发射.某中学科技兴趣小组为了解本校学生对航天科技的关注程度,将“关注程度”分为四类:A类为“非常关注”,B类为“比较关注”,C类为“关注”,D类为“不关注”.该小组在校内进行了随机调查,并将调查结果绘制成如下两幅统计图,请根据统计图中的信息解答下列问题: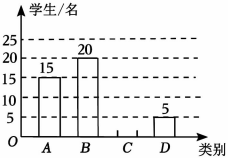
 (1)、 补全条形统计图;(2)、扇形统计图中,A类对应扇形的圆心角度数为;(3)、该校共有1200名学生,根据调查结果估计该校“关注”“比较关注”及“非常关注”的学生共多少名?21. 2023年9月,第19届亚运会在杭州举行,本届亚运会吉祥物“宸宸”“琮琮”“莲莲”是一组承载深厚底蕴和充满时代活力的机器人.某纪念品店购进了一批亚运会吉祥物,其中“琮琮”“莲莲”共100个,花费4400元,这两种吉祥物的进价和售价如下表:
(1)、 补全条形统计图;(2)、扇形统计图中,A类对应扇形的圆心角度数为;(3)、该校共有1200名学生,根据调查结果估计该校“关注”“比较关注”及“非常关注”的学生共多少名?21. 2023年9月,第19届亚运会在杭州举行,本届亚运会吉祥物“宸宸”“琮琮”“莲莲”是一组承载深厚底蕴和充满时代活力的机器人.某纪念品店购进了一批亚运会吉祥物,其中“琮琮”“莲莲”共100个,花费4400元,这两种吉祥物的进价和售价如下表:吉祥物名称
琮琮
莲莲
进价(元/个)
40
50
售价(元/个)
60
65
 (1)、该纪念品购进“琮琮”和“莲莲”各多少个?(2)、在(1)问的情况下,若把所购进的“琮琮”“莲莲”两种吉祥物全部销售完,利润率能否超过40%?请说明理由.22. 如图,是的平分线,是的平分线.
(1)、该纪念品购进“琮琮”和“莲莲”各多少个?(2)、在(1)问的情况下,若把所购进的“琮琮”“莲莲”两种吉祥物全部销售完,利润率能否超过40%?请说明理由.22. 如图,是的平分线,是的平分线.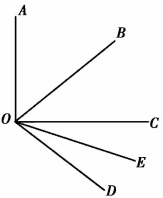 (1)、若 , , 则;(2)、若 , 求的度数.23. 定义如下:使等式成立的一对有理数叫“理想有理数对”,记为 , 如: , 所以数对是“理想有理数对”.(1)、判断数对是否为“理想有理数对”,并说明理由;(2)、若数对是“理想有理数对”,求代数式的值.24. 数轴是数学中的一个重要工具,利用数轴可以将数与形进行完美的结合,如:数轴上点表示的数为 , 点表示的数为 , 则两点之间的距离为 . 如图所示,点为数轴上的三个点,表示的数分别为 , 满足 , 且为的倒数.动点 , 分别从点出发,分别以每秒1个单位长度和4个单位长度的速度向右运动,动点从点出发,以每秒3个单位长度的速度向左运动,三个动点同时出发,设运动的时间为秒(),请回答下列问题:(1)、直接写出的值: , , ;(2)、当时,求的值;(3)、在运动过程中,的值是否发生变化?若发生变化,请用含的式子表示;若不发生变化,请求出的值.
(1)、若 , , 则;(2)、若 , 求的度数.23. 定义如下:使等式成立的一对有理数叫“理想有理数对”,记为 , 如: , 所以数对是“理想有理数对”.(1)、判断数对是否为“理想有理数对”,并说明理由;(2)、若数对是“理想有理数对”,求代数式的值.24. 数轴是数学中的一个重要工具,利用数轴可以将数与形进行完美的结合,如:数轴上点表示的数为 , 点表示的数为 , 则两点之间的距离为 . 如图所示,点为数轴上的三个点,表示的数分别为 , 满足 , 且为的倒数.动点 , 分别从点出发,分别以每秒1个单位长度和4个单位长度的速度向右运动,动点从点出发,以每秒3个单位长度的速度向左运动,三个动点同时出发,设运动的时间为秒(),请回答下列问题:(1)、直接写出的值: , , ;(2)、当时,求的值;(3)、在运动过程中,的值是否发生变化?若发生变化,请用含的式子表示;若不发生变化,请求出的值.