贵州省毕节市威宁彝族回族苗族自治县2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-03-21 类型:期末考试
一、选择题(本大题共12小题,每小题3分,共36分,每小题四个选项,其中只有一个是正确的)
-
1. 方程的解为( )A、 B、 C、或-4 D、或42. 如图,转盘中四个扇形的面积都相等,小明随意转动转盘1次,指针指向的数字为偶数的概率为( )
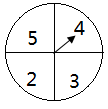 A、 B、 C、 D、3. 已知 , 若 , 则=( )A、12 B、15 C、16 D、14. 在同一平面直角坐标系中,函数与的图象可能是( )A、
A、 B、 C、 D、3. 已知 , 若 , 则=( )A、12 B、15 C、16 D、14. 在同一平面直角坐标系中,函数与的图象可能是( )A、 B、
B、 C、
C、 D、
D、 5. 顺次连接矩形各边中点所得的四边形一定是( )A、梯形 B、矩形 C、菱形 D、正方形6. 一个三角形的两边长是2和6,第三边长是方程的根,则这个三角形的周长为( )A、15 B、11 C、11或15 D、无法确定7. 下列四个几何体中,主视图为圆的是( )A、
5. 顺次连接矩形各边中点所得的四边形一定是( )A、梯形 B、矩形 C、菱形 D、正方形6. 一个三角形的两边长是2和6,第三边长是方程的根,则这个三角形的周长为( )A、15 B、11 C、11或15 D、无法确定7. 下列四个几何体中,主视图为圆的是( )A、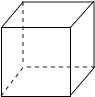 B、
B、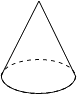 C、
C、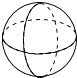 D、
D、 8. 在一个晴朗的上午,乐乐拿着一块长方形木板在地面上形成的投影中不可能是( )A、
8. 在一个晴朗的上午,乐乐拿着一块长方形木板在地面上形成的投影中不可能是( )A、 B、
B、 C、
C、 D、
D、 9. 已知关于的一元二次方程有一个根为0,则=( )A、±1 B、1 C、0 D、-110. 一个家庭有两个孩子,两个都是女孩的概率是( )A、 B、 C、 D、无法确定11. 如图,在长为8cm,宽为4cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形的面积是( )
9. 已知关于的一元二次方程有一个根为0,则=( )A、±1 B、1 C、0 D、-110. 一个家庭有两个孩子,两个都是女孩的概率是( )A、 B、 C、 D、无法确定11. 如图,在长为8cm,宽为4cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形的面积是( ) A、 B、 C、 D、12. 如图,将个边长都为2的正方形按如图所示摆放,点 , , …,分别是正方形的中心,则这个正方形重叠部分的面积之和是( )
A、 B、 C、 D、12. 如图,将个边长都为2的正方形按如图所示摆放,点 , , …,分别是正方形的中心,则这个正方形重叠部分的面积之和是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共4小题,每小题4分,共16分)
-
13. 已知 是反比例函数,那么k的值是 .14. 两个三角形相似,其中一个三角形的两个内角是40°、60°,那么另一个三角形的最大内角是度.15. 如图,在菱形中, , , 则菱形的周长为 .
 16. 如图,在中, , , , 绕顶点逆时针旋转到处,此时线段与的交点为的中点,则线段的长度为 .
16. 如图,在中, , , , 绕顶点逆时针旋转到处,此时线段与的交点为的中点,则线段的长度为 .
三、解答题(本大题共9小题,共98分)
-
17. 解方程.(1)、(2)、18. 画出以下两个几何体的三视图.(1)、
 (2)、
(2)、 19. 如图,已知 , .
19. 如图,已知 , . (1)、求证:;(2)、若 , , 求的长.20. 甲、乙两个盒子中装有质地、大小相同的小球,甲盒中有2个白球、1个黄球和1个蓝球;乙盒中有1个白球、2个黄球和若干个蓝球.从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的2倍.(1)、求乙盒中蓝球的个数.(2)、从甲、乙两盒中分别任意摸取一球,利用列表或画树状图法求这两球均为蓝球的概率.21. 如图,小明为了测量一大楼的高度,在地面上放一平面镜,镜子与大楼的距离 , 他与镜子的距离是2m时,刚好能从镜子中看到楼顶 , 已知他的眼睛到地面的高度为1.6m,结果他很快计算出大楼的高度 , 你知道有多高吗?请加以说明.
(1)、求证:;(2)、若 , , 求的长.20. 甲、乙两个盒子中装有质地、大小相同的小球,甲盒中有2个白球、1个黄球和1个蓝球;乙盒中有1个白球、2个黄球和若干个蓝球.从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的2倍.(1)、求乙盒中蓝球的个数.(2)、从甲、乙两盒中分别任意摸取一球,利用列表或画树状图法求这两球均为蓝球的概率.21. 如图,小明为了测量一大楼的高度,在地面上放一平面镜,镜子与大楼的距离 , 他与镜子的距离是2m时,刚好能从镜子中看到楼顶 , 已知他的眼睛到地面的高度为1.6m,结果他很快计算出大楼的高度 , 你知道有多高吗?请加以说明. 22. 如图,已知反比例函数的图象与一次函数的图象交于和两点.
22. 如图,已知反比例函数的图象与一次函数的图象交于和两点. (1)、求这两个函数的表达式;(2)、求的面积;
(1)、求这两个函数的表达式;(2)、求的面积;
(3)、请判断点是否在这个反比例函数的图象上,并说明理由;(4)、根据图象写出使反比例函数的值大于一次函数的值的的取值范围.23. 西瓜经营户以3元/千克的价格购进一批小型西瓜,以4元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本共24元.该经营户要想每天盈利200元,应将每千克这种小型西瓜的售价降低多少元?24. 自深圳经济特区建立至今50年以来,深圳本土诞生了许多优秀的科技企业,华为、腾讯、中兴、大疆就是其中的四个杰出代表.某数学兴趣小组在校内对这四个企业进行“你最认可的特区科技企业”调查活动.兴趣小组随机调查了人(每人必选一个且只能选一个),并将调查结果绘制成了如下尚不完整的统计图,请根据图中信息回答以下问题: (1)、请将以上两个统计图补充完整;(2)、= , “腾讯”所在扇形的圆心角的度数为;(3)、该校共有2000名同学,估计最认可“华为”的同学大约有名;(4)、已知 , 两名同学都最认可“华为”,同学最认可“腾讯”,同学最认可“中兴”,从这四名同学中随机抽取两名同学,请你利用画树状图或列表的方法求出这两名同学最认可的特区科技企业不一样的概率.25. 定义:长宽比为(n为正整数)的矩形称为矩形.下面,我们通过折叠的方式折出一个矩形,如图①所示.
(1)、请将以上两个统计图补充完整;(2)、= , “腾讯”所在扇形的圆心角的度数为;(3)、该校共有2000名同学,估计最认可“华为”的同学大约有名;(4)、已知 , 两名同学都最认可“华为”,同学最认可“腾讯”,同学最认可“中兴”,从这四名同学中随机抽取两名同学,请你利用画树状图或列表的方法求出这两名同学最认可的特区科技企业不一样的概率.25. 定义:长宽比为(n为正整数)的矩形称为矩形.下面,我们通过折叠的方式折出一个矩形,如图①所示.操作1:将正方形沿过点的直线折叠,使折叠后的点落在对角线上的点处,折痕为 .
操作2:将沿过点的直线折叠,使点 , 点分别落在边 , 上,折痕为 .
则四边形为矩形.
证明:设正方形的边长为1,则 .
由折叠性质可知 , , 则四边形为矩形,
∴ , ∴ .
∴ , 即 , ∴ , ∴ ,
∴四边形为矩形.

阅读以上内容,回答下列问题:
(1)、在图①中,所有与相等的线段是、 , 的值是;(2)、已知四边形为矩形,模仿上述操作,得到四边形 , 如图②,求证:四边形为矩形;(3)、将图②中的矩形沿用(2)中的方式操作3次后,得到一个“矩形”,则的值是 .