2023-2024学年初中数学湘教版七年级下学期第1章二元一次方程组单元测试 A卷

试卷更新日期：2024-03-21 类型：单元试卷

进入出卷网下载

一、选择题

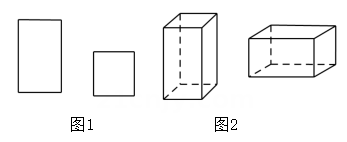
1. 下列方程属于二元一次方程的是（）

A、 $x + \frac{2}{y} = 1$ B、3-2xy=1 C、 $\frac{x + y}{3} - 2 y = 0$ D、3-2x=1

查看试题解析
2. 方程组 $\{\begin{matrix} 2 x + y = 4 ， \\ x - y = - 1 \end{matrix}$ 的解为（）

A、 $\{\begin{matrix} x = 1 ， \\ y = 2 \end{matrix}$ B、 $\{\begin{matrix} x = - 3 ， \\ y = - 2 \end{matrix}$ C、 $\{\begin{matrix} x = 2 ， \\ y = 0 \end{matrix}$ D、 $\{\begin{matrix} x = 3 ， \\ y = - 1 \end{matrix}$

查看试题解析
3. 《孙子算经》是中国古代重要的数学著作，成书大约在一千五百年前.其中一道题，原文是：“今三人共车，两车空；二人共车，九人步.问人与车各几何？”意思是：现有若干人和车，若每辆车乘坐3人，则空余两辆车：若每辆车乘坐2人，则有9人步行，问人与车各多少？设有 $x$ 人， $y$ 辆车，可列方程组为（）

A、 ${\begin{array}{l} \frac{x}{3} = y + 2 \\ \frac{x}{2} + 9 = y \end{array}$ B、 ${\begin{array}{l} \frac{x}{3} = y - 2 \\ \frac{x - 9}{2} = y \end{array}$ C、 ${\begin{array}{l} \frac{x}{3} = y + 2 \\ \frac{x - 9}{2} = y \end{array}$ D、 ${\begin{array}{l} \frac{x}{3} = y - 2 \\ \frac{x}{2} - 9 = y \end{array}$

查看试题解析
4. 由方程组 ${\begin{array}{l} 2 x + m = 1 \\ m = y - 3 \end{array}$ ，可得x与y的关系是（）

A、2x+y=4 B、2x+y=-4 C、2x-y=4 D、2x-y=-4

查看试题解析
5. 若 ${\begin{array}{l} x = 2 \\ y = - 1 \end{array}$ 是下列某二元一次方程组的解，则这个方程组为（）

A、 ${\begin{array}{l} x + 3 y = 5 \\ x + y = 1 \end{array}$ B、 ${\begin{array}{l} 2 x - y = 5 \\ x + y = 1 \end{array}$ C、 ${\begin{array}{l} x = 2 y \\ x = 3 y + 1 \end{array}$ D、 ${\begin{array}{l} x = y - 3 \\ y + 2 x = 5 \end{array}$

查看试题解析
6. 已知 $\{\begin{matrix} x = 1 \\ y = - 1 \end{matrix}$ 是方程2x-ay=3的一个解，那么a的值是( )

A、1 B、3 C、-3 D、-1

查看试题解析
7. 若方程组 $\{\begin{matrix} a_{1} x + b_{1} y = c_{1} ， \\ a_{2} x + b_{2} y = c_{2} \end{matrix}$ 的解为 $\{\begin{matrix} x = 4 ， \\ y = 6 ， \end{matrix}$ 则方程组 $\{\begin{matrix} 4 a_{1} x + 3 b_{1} y = 5 c_{1} ， \\ 4 a_{2} x + 3 b_{2} y = 5 c_{2} \end{matrix}$ 的解为（）

A、 $\{\begin{matrix} x = 4 ， \\ y = 6 \end{matrix}$ B、 $\{\begin{matrix} x = 5 ， \\ y = 6 \end{matrix}$ C、 $\{\begin{matrix} x = 5 ， \\ y = 10 \end{matrix}$ D、 $\{\begin{matrix} x = 10 ， \\ y = 15 \end{matrix}$

查看试题解析
8. 为了增强学生的安全防范意识，某校举行了一次安全知识抢答赛，抢答题一共20个，记分规则如下：每答对一个得5分，每答错或不答一个扣1分.小红一共得到 70分，则小红答对的题的个数为（）

A、14 B、15 C、16 D、17

查看试题解析
9. 分别用如图1所示的长方形和正方形纸板作侧面和底面，做成如图2所示的竖式和横式的两种无盖纸盒.现有m张正方形纸板和n张长方形纸板，如果做两种纸盒若干个，恰好将纸板用完，则m+n的值可能是（）

A、2022 B、2023 C、2024 D、2025

查看试题解析
10. 如果方程组 $\{\begin{matrix} x + y = ✭ \\ 2 x + y = 16 \end{matrix}$ 的解为 $\{\begin{matrix} x = 6 ， \\ y = ■ ， \end{matrix}$ 那么被“★”“■”遮住的两个数分别为（）

A、10，4 B、4，10 C、3，10 D、10，3

查看试题解析

二、填空题

11. 写出一个以 ${\begin{cases} x = 1 \\ y = 2 \end{cases}$ 为解的二元一次方程组，可以是

查看试题解析
12. 如图，射线OC的端点O在直线AB上，∠1的度数x°比∠2的度数y°的2倍多10°，则列出关于x，y的方程组是

查看试题解析
13. 中国古代数学著作《算法统宗》中记载了这样一个题目：“九百九十九文钱，甜果苦果买一千，四文钱买苦果七，十一文钱九个甜，甜苦两果各几个?”其大意是：用九百九十九文钱共买了一千个苦果和甜果，其中四文钱可以买七个苦果，十一文钱可以买九个甜果.问：苦、甜果各有几个?设苦果有x个，甜果有y个，则可列方程组为.

查看试题解析
14. 在长为12m、宽为9m的长方形空地上，沿平行于长方形各边的方向分割出三个形状、大小一样的小长方形花圃(如图)，则小长方形花圃的长为m.

查看试题解析
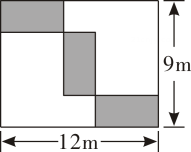15. 如图，已知前两架天平两端保持平衡.要使第三架天平两端保持平衡，则应在天平的右托盘上放个圆形物品.

查看试题解析
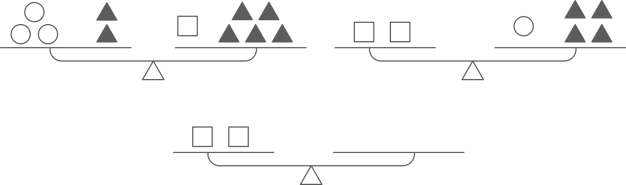16. 已知关于x，y的方程组 $\{\begin{matrix} x + 2 y = k ， \\ 2 x + 3 y = 3 k - 1 ， \end{matrix}$ 有以下结论：
①当k=0时，方程组的解为 $\{\begin{matrix} x = - 2 ， \\ y = 1 ； \end{matrix}$ ②方程组的解可表示为 $\{\begin{matrix} x = 3 k - 2 ， \\ y = 1 - k ； \end{matrix}$ ③不论k取什么实数，x+3y的值始终不变.
其中正确的是（填序号）.

查看试题解析

三、计算题

17. 解下列方程组：

(1)、 $\{\begin{matrix} 3 x + y = 8 ， \\ x - y = 4 . \end{matrix}$

(2)、 $\{\begin{matrix} x + 4 y = 14 ， \\ \frac{x - 3}{4} - \frac{y - 3}{3} = \frac{1}{12} . \end{matrix}$

查看试题解析
18. 解下列方程组：

(1)、 $\{\begin{matrix} x - y = 2 ， \\ 3 x + 2 y = 11 . \end{matrix}$

(2)、 $\{\begin{cases} 8 x + 9 y = 6 ， \\ \frac{4 x}{5} + \frac{5 y}{6} = \frac{7}{15} . \end{cases}$

查看试题解析

四、解答题

19. 已知 $\{\begin{matrix} x = 1 ， \\ y = - 2 \end{matrix}$ 是二元一次方程组 $\{\begin{matrix} a x - 2 y = 0 ， \\ 2 b x + a y = 2 \end{matrix}$ 的解.求：

(1)、a，b的值.

(2)、方程组 $\{\begin{matrix} a (2 x + 1) - 2 (3 y - 5) = 0 ， \\ 2 b (2 x + 1) + a (3 y - 5) = 2 \end{matrix}$ 的解.

查看试题解析
20. 某商店将甲、乙、丙三种糖果混合制成什锦糖，并以糖的平均价格(三种糖果的总价除以它们的质量和)作为什锦糖的单价.若购买10千克甲种糖果和20千克乙种糖果共需费用650元，购买20千克甲种糖果和10千克乙种糖果共需费用700元.

(1)、求甲、乙两种糖果的单价.

(2)、设丙种糖果的单价为15元/千克，且甲、乙、丙三种糖果的质量之比为1：2：a，若什锦糖的单价为20元/千克，求a的值.

查看试题解析
21. 如图，在大长方形 ABCD中，放入6个相同的小长方形，已知BC=11，DE=7.

(1)、设每个小长方形的长为x，宽为y，求x，y的值.

(2)、求图中阴影部分的面积.

查看试题解析

五、实践探究题

22. 注意：为了使同学们更好地解答本题，我们提供了一种解思路，你可以依照这个思路接下面的要求填空，完成本题的解答．也可以选用其他的解题方案，此时不必填空，只需按照解答题的一般要求进行解答．
某茶叶店经销A，B两种茶，第一次购进了A种茶 $30$ 盒，B种茶 $20$ 盒，共花费 $7000$ 元；第二次购进时，两种茶每盒的价格都提高了 $20 %$ ，该店又购进了A种茶 $20$ 盒，B种茶 $15$ 盒，共花费 $6000$ 元，求第一次购进的A，B两种茶每盒的价格．
解题方案：设第一次购进的A种茶每盒的价格为x元，B种茶每盒的价格为y元．

(1)、根据题章，列出方程组 ${\begin{array}{l} ____________ \\ ____________ \end{array}$ ；

(2)、解这个方程组，得 ${\begin{array}{l} x =____________ \\ y =____________ \end{array}$ ．
答：第一次购进的A种茶每盒的价格为元，B种茶每盒的价格为元．

查看试题解析
23. 请同学们根据以下表格中的素材一和素材二，自主探索完成任务一、任务二、任务三．
素材一：为促进消费，某市人民政府决定，发放“双促双旺 $\cdot$ 你消费我助力”消费券，一人可领取的消费券有： $A$ 型消费券 $($ 满 $35$ 减 $15$ 元 $) 2$ 张， $B$ 型消费券 $($ 满 $68$ 减 $25$ 元 $) 2$ 张， $c$ 型消费券 $($ 满 $158$ 减 $60$ 元 $) 1$ 张．

素材二：在此次活动中，小明一家 $5$ 人每人都领到了所有的消费券 $.$ 某日小明一家在超市使用消费券，消费金额减了 $390$ 元，请完成以下任务．

如何合理搭配消费券？

(1)、任务一：若小明一家用了 $5$ 张 $A$ 型消费券， $3$ 张 $B$ 型的消费券，则用了张 $C$ 型的消费券，此时的实际消费最少为元 $.$

(2)、任务二：若小明一家用 $13$ 张 $A$ 、 $B$ 、 $C$ 型的消费券消费，已知 $A$ 型比 $C$ 型的消费券多 $1$ 张，求 $A$ 、 $B$ 、 $C$ 型的消费券各多少张？

(3)、任务三：若小明一家仅用两种不同类型的消费券消费，请问如何搭配使用消费券，使得使用付款最少，并求出此时消费券的搭配方案．

查看试题解析
24. 【阅读理解】阅读下列解方程组的方法，然后解决问题．
解方程组 ${\begin{array}{l} 16 x + 14 y = 170 ① \\ 14 x + 16 y = 130 ② \end{array}$ 时，如果直接考虑消元，那么非常麻烦，而采用下列解法则轻而易举．
解：①＋②， $30 x + 30 y = 300$ ，
即 $x + y = 10$ ③
①－②， $2 x - 2 y = 40$
即 $x - y = 20$
联立③和④，得 ${\begin{array}{l} x + y = 10 ① \\ x - y = 20 ② \end{array}$
解得 ${\begin{array}{l} x = 15 \\ y = - 5 \end{array}$
所以原方程组的解为 ${\begin{array}{l} x = 15 \\ y = - 5 \end{array}$

(1)、由二元一次方程组 ${\begin{array}{l} 2 x + 3 y = 6 \\ 3 x + 2 y = 4 \end{array}$ ，可得 $x + y =$ ； $x - y =$ ．

(2)、解方程组 ${\begin{array}{l} 2024 x + 2025 y = 2023 \\ 2022 x + 2023 y = 2021 \end{array}$

(3)、【拓展提升】
对于实数x ， y ，定义新运算： $x * y = a x + b y + c$ ，其中a ， b ， c是常数，例如： $5 * 6 = 5 a + 6 b + c$ ．
已知 $2 * 4 = 15 ， 3 * 7 = 27$ ，则 $1 * 1 =$ ．

查看试题解析

六、综合题

25. 阅读以下内容，并回答问题：
用代入法解方程组 $\{\begin{matrix} 7 x - 2 y = 3 ， ① \\ x - 2 y = - 12 ， ② \end{matrix}$ 有以下步骤：
解：由①，得 $y = \frac{7 x - 3}{2}$ .③ 第一步
把③代入①，得 $7 x - 2 \times \frac{7 x - 3}{2} = 3 .$ 第二步
整理得3=3. 第三步
∴x可取一切实数，原方程组有无数个解. 第四步

(1)、以上解法中，出现错误的是第步.

(2)、用加减法解这个方程组.

查看试题解析
26. 某电器商场销售A、B两种型号计算器，两种计算器的进货价格分别为每台30元、40元．商场销售5台A型号和1台B型号计算器，可获利润76元；销售6台A型号和3台B型号计算器，可获利润120元．（利润＝销售价格-进货价格）

(1)、求商场销售A、B两种型号计算器的销售价格分别是多少元？（列方程或方程组解决）

(2)、商场推出两种优惠套餐供顾客选择：
套餐一：A、B两种型号计算器均打八折出售；
套餐二：A型号计算器打九折出售，B型号计算器打七折出售．
现学校需要购买A、B两种型号计算器共420台，学校选择哪个优惠套餐购买更划算？

查看试题解析

2023-2024学年初中数学湘教版七年级下学期 第1章 二元一次方程组 单元测试 A卷

一、选择题

二、填空题

三、计算题

四、解答题

五、实践探究题

六、综合题

2023-2024学年初中数学湘教版七年级下学期第1章二元一次方程组单元测试 A卷