湖南省岳阳市2024届高三上学期教学质量监测（一模）物理试题

试卷更新日期：2024-03-20 类型：高考模拟

进入出卷网下载

一、选择题：本题共6小题，每小题4分，共24分。在每小题给出的四个选项中，只有一项符合题目要求。

1. 在物理学的发展过程中，科学家们总结出了许多物理学研究方法，以下关于物理学研究方法的叙述正确的是（　　）

A、在不需要考虑带电物体本身的大小和形状时，用点电荷来代替物体的方法叫微元法 B、在推导匀变速直线运动位移公式时，把整个运动过程划分成很多小段，每一小段近似看作匀速直线运动，然后把各小段的位移相加，这里采用了理想模型法 C、演绎推理是从一般性结论推出个别性结论的方法，即从已知的某些一般原理、定理、法则、公理或科学概念出发，推出新结论的一种思维活动。比如，楞次定律的得出用的就是演绎推理的方法 D、物理概念是运用抽象、概括等方法进行思维加工的产物。科学前辈就是在追寻不变量的努力中，通过抽象、概括等方法提出了动量的概念

查看试题解析
2. 丹麦物理学家奥斯特发现了电流的磁效应，揭开了人类研究电磁间关系的序幕。三根相互平行的通电长直导线a、b、c电流均为I，如图所示放在等腰直角三角形三个顶点上，每根通电直导线单独存在时，O点的磁感应强度都是B，则三根通电导线同时存在时O点的磁感应强度的大小为（）

A、 $\sqrt{5}$ B B、3B C、 $2 \sqrt{2}$ B D、B

查看试题解析
3. 如图甲所示，小明在地球表面进行了物体在竖直方向做直线运动的实验，弹簧原长时，小球由静止释放，在弹簧弹力与重力作用下，测得小球的加速度a与位移x的关系图像如图乙所示。已知弹簧的劲度系数为k，地球的半径为R，万有引力常量为G，不考虑地球自转影响，忽略空气阻力，下列说法正确的是（）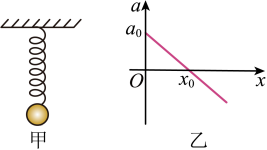

A、小球的位移为x₀时，小球正好处于完全失重状态 B、小球的最大速度为 $\sqrt{a_{0} x_{0}}$ C、小球的质量为 $\frac{k x_{0}}{2 a_{0}}$ D、地球的密度为 $\frac{3 a_{0}}{2 π G R}$

查看试题解析
4. 如图所示四幅图为物体做直线运动的图像，下列说法正确的是（　　）

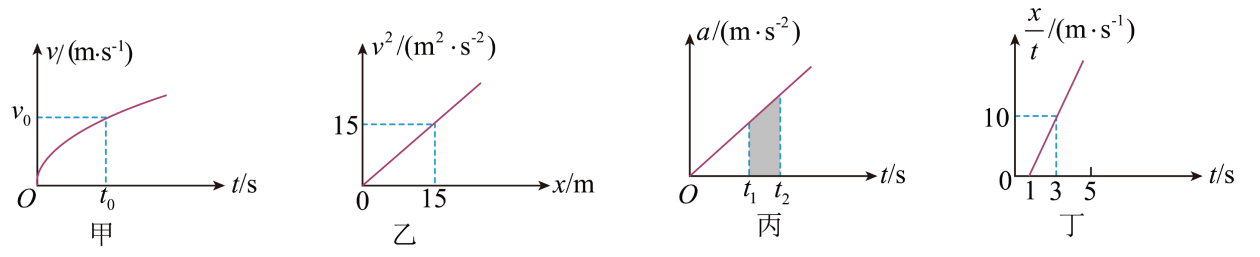A、甲图中，物体在0~t₀时间内的位移等于 $\frac{v_{0} t_{0}}{2}$ B、乙图中，物体的加速度大小为1m/s² C、丙图中，阴影面积表示t₁~t₂时间内物体的加速度变化量 D、丁图中t=4s时物体的速度大小为35m/s

查看试题解析
5. 如图所示，真空中有一边长为l的正六边形ABCDFG，O为正六边形中心，在A、B、C三点分别固定电荷量为q、-2q、q（q>0）的三个点电荷。已知点电荷Q的电势公式 $φ = \frac{k Q}{r}$ ，其中k为静电常量，Q为场源电荷的电荷量，r为某点到Q的距离，取无穷远处电势为零。则下列说法正确的（　　）

A、O点电势为负 B、D点和G点场强相同 C、O点的电场强度大小为 $k \frac{q}{l^{2}}$ ，方向由O指向B D、把一带负电的试探电荷从O点移至F点，其电势能变大

查看试题解析
6. 某款手机“弹球游戏”可简化为如图所示。游戏者将小球（视为质点）以某个初速度垂直墙壁水平射出，在与台阶、竖直墙的碰撞不超过两次的前提下，击中第三级台阶的水平面MN段为通关。已知台阶的宽和高均为d，以v₀射出时恰击中第一级台阶的末端，所有碰撞均为弹性碰撞，以下说法正确的是（　　）

A、以v₀射出时，小球在空中的运动时间为 $\frac{3 d}{v_{0}}$ B、以2v₀射出时不能通关 C、若小球的初速度v的满足 $\sqrt{2} v_{0} < v \leq \sqrt{3} v_{0}$ 时，可直接击中第三级台阶MN段 D、若利用墙面且仅反弹一次击中第三级台阶的水平面，碰撞点距N点高度须小于 $\frac{27}{16} d$

查看试题解析

二、选择题：本题共4小题，每小题5分，共20分。在每小题给出的四个选项中，有多项符合题目要求。全部选对的得5分，选对但不全的得3分，有选错的得0分。

7. 如图所示，矩形盒内用两根不可伸长的轻线固定一个质量为 $m = 0.6 k g$ 的匀质小球，a线与水平方向成37°角，b线水平。两根轻线所能承受的最大拉力都是 $F_{m} = 15 N$ ，已知 $s i n 37 ° = 0.6$ ， $c o s 37 ° = 0.8$ ，取 $g = 10 m / s^{2}$ ，则（　　）

A、系统静止时，a线所受的拉力大小12Nb B、系统静止时，b线所受的拉力大小8N C、当系统沿竖直方向匀加速上升时，为保证轻线不被拉断，加速度最大为5m/s² D、当系统沿水平方向向右匀加速时，为保证轻线不被拉断，加速度最大为10m/s²

查看试题解析
8. 图甲起重机某次从 $t = 0$ 时刻由静止开始提升质量为 $m = 150 k g$ 的物体，其 $a - t$ 图像如图乙所示，5~10s内起重机的功率为额定功率，不计其它阻力，重力加速度为 $g = 10 m / s^{2}$ ，则以下说法正确的是（　　）

A、物体在0~10s内运动的最大速度为10m/s B、起重机的额定功率为18000W C、5~10s内起重机对物体做的功等于0~5s内起重机对物体做功的1.5倍 D、5~10s内起重机对物体做的功等于0~5s内起重机对物体做功的2倍

查看试题解析
9. 如图所示，轻质弹簧一端固定在水平面上光滑转轴O上，另一端与套在粗糙固定直杆N处质量为0.2kg的小球（可视为质点）相连。直杆与水平面的夹角为30°，N点距水平面的高度为0.4m，NP=PM，ON=OM，OP等于弹簧原长。小球从N处由静止开始下滑，经过P处的速度为2m/s，并恰能停止在M处。已知重力加速度取10m/s² ，小球与直杆的动摩擦因数为 $\frac{\sqrt{3}}{5}$ ，则下列说法正确的是（　　）

A、小球通过P点时的加速度大小为3m/s² B、弹簧具有的最大弹性势能为0.5J C、小球通过NP段与PM段摩擦力做功相等 D、N到P过程中，球和弹簧组成的系统损失的机械能为0.4J

查看试题解析
10. 如图所示，两根足够长光滑平行金属导轨固定在倾角θ=37°的绝缘斜面上，底部接有一阻值R=2Ω的定值电阻，轨道上端开口，间距L=1m，整个装置处于磁感应强度B=2T的匀强磁场中，磁场方向垂直斜面向上。质量m=0.2kg的金属棒ab置于导轨上，通过细线（细线与导轨平行）经定滑轮与质量为M=0.2kg的小物块相连。金属棒ab在导轨间的电阻r=1Ω，导轨电阻不计。金属棒由静止释放到匀速运动前，电阻R产生的焦耳热总共为1.552J，金属棒与导轨接触良好，不计空气阻力，sin37°=0.6，cos37°=0.8，g=10m/s² ，则下列说法正确的（　　）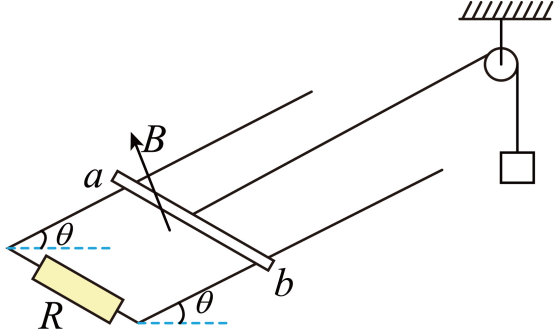

A、金属棒ab匀速运动时速度大小为0.6m/s B、金属棒ab沿导轨运动过程中，电阻R上的最大电功率为0.36W C、金属棒从开始运动到最大速度沿导轨运动的距离2m D、从金属棒ab开始运动至达到最大速度过程中，流过电阻R的总电荷量为2C

查看试题解析

三、非选择题：本题共5小题，共56分。

11. 某小组为了验证机械能守恒定律，设计了如图甲所示的实验装置，物块P、Q用跨过定滑轮的轻绳相连，P底端固定一宽度为d的轻质遮光条，托住P，用刻度尺测出遮光条所在位置A与固定在铁架台上的光电门B之间的高度差h（ $d ≪ h$ ）。已知当地的重力加速度为g。

(1)、用游标卡尺测量遮光条的宽度d如图丙所示，则图丙中游标卡尺的读数应为cm。

(2)、下列实验步骤正确的是____

A、选择两个质量相等的物块进行实验 B、实验时，要确保物块P由静止释放 C、需要测量出两物块的质量m_P和m_Q D、需要测量出遮光条从A到达B所用的时间T

(3)、改变高度h，重复实验，测得各次遮光条的挡光时间t，以h为横轴、 $\frac{1}{t^{2}}$ 为纵轴建立平面直角坐标系，在坐标系中作出 $\frac{1}{t^{2}} - h$ 图像，如图丙所示，该图像的斜率为k，在实验误差允许范围内，若k=（用题中字母表示），则验证了机械能守恒定律。

查看试题解析
12. 某实验小组利用如下器材测定一电压表的量程U_x和内阻R_x；
待测电压表V₁（量程约0~3.0V，内阻约为3k Ω）
标准电压表V₂（量程0~6.0V，内阻约为20k Ω）
滑动变阻器R（最大阻值50Ω）
电阻箱R（0~9999.9Ω）
直流电源E（7.5V.有内阻）
开关S及导线若干
回答下列问题：

(1)、现用多用电表测电压表V₁的内阻，选择倍率“×100”挡，其它操作无误，多用电表表盘示数如图甲，则电压表V₁的内阻约为。

(2)、图丙是该实验小组未完成的实物连线图，请你根据图乙原理图完成实物连线。

(3)、闭合开关S，调节滑动变阻器和电阻箱的阻值，保证V₁满偏，记录V₂的示数U₂和电阻箱的阻值R，断开开关。多次重复上述操作。根据多次测得的数值在 $U_{2} - R$ 坐标系中描点，如图丁。请根据坐标系中的描点作出 $U_{2} - R$ 图线。

(4)、根据图丁中图线求得V₁的量程U_x＝V，内阻R_x＝。（结果均保留两位有效数字）

查看试题解析
13. 如图，在倾角37°足够长的斜面上有一个质量为1kg的物体，物体与斜面之间的动摩擦因数为0.25。物体在拉力F的作用下从斜面底端由静止开始运动，F的大小为10N方向沿斜面向上。已知 $s i n 37 ° = 0.6$ ， $c o s 37 ° = 0.8$ ，取 $g = 10 m / s^{2}$ ，求：

(1)、物体的加速度大小？

(2)、加速2s后撤去F，让物体在斜面上运动，物体静止开始在斜面上运动的整个过程中因摩擦产生的热量是多少？

查看试题解析
14. 如图所示，在xOy坐标系中，x轴上方有一圆形匀强磁场区域，其圆心为O₁（0，2m）、半径R=2m，磁感应强度 $B = 2 \times 1 0^{- 2} T$ ，方向垂直于纸面向外。在x轴下方有匀强电场，电场强度 $E = 0.2 N / C$ ，方向水平向左。在磁场的左侧 $0.5 R \leq y \leq 1.5 R$ 区域内，有一群质量 $m = 4 \times 1 0^{- 6} k g$ 、电荷量 $q = + 2 \times 1 0^{- 2} C$ 的粒子以速度 $v = 2 \times 1 0^{2} m / s$ 平行于x轴正方向且垂直于磁场射入圆形磁场区域。不计粒子的重力和粒子间的相互作用。求：（结果可用含π和根号的式子表示）

(1)、粒子在磁场区域运动的轨迹半径r；

(2)、粒子在磁场区域运动的最长时间t；

(3)、粒子打在y轴上离原点O的最远距离d，以及粒子的最大电势能（取坐标原点电势为0）。

查看试题解析
15. 如图所示，足够长的水平光滑直轨道AB和水平传送带平滑无缝连接，传送带长L=4m，以10m/s的速度顺时针匀速转动，带有光滑圆弧管道EF的装置P固定于水平地面上，EF位于竖直平面内，由两段半径均为R=0.8m的 $\frac{1}{4}$ 圆弧细管道组成，EF管道与水平传送带和水平地面上的直轨道MN均平滑相切连接，MN长L₂=2m，右侧为竖直墙壁。滑块a的质量m₁=0.3kg，滑块b与轻弹簧相连，质量m₂=0.1kg，滑块c质量m₃=0.6kg，滑块a、b、c均静置于轨道AB上。现让滑块a以一定的初速度水平向右运动，与滑块b相撞后立即被粘住，之后与滑块c发生相互作用，c与劲度系数k=1.5N/m的轻质弹簧分离后滑上传送带，加速之后经EF管道后滑上MN。已知滑块c第一次经过E时对轨道上方压力大小为42N，滑块c与传送带间的动摩擦因数μ₁=0.35，与MN间的动摩擦因数μ₂=0.4，其它摩擦和阻力均不计，滑块与竖直墙壁的碰撞为弹性碰撞，各滑块均可视为质点，重力加速度大小g=10m/s² ，弹簧的弹性势能 $E_{p} = \frac{1}{2} k x^{2}$ （x为形变量）。求：

(1)、滑块c第一次经过F点时速度大小（结果可用根号表示）；

(2)、滑块a的初速度大小v₀：

(3)、试通过计算判断滑块c能否再次与弹簧发生相互作用，若能，求出弹簧第二次压缩时最大的压缩量。

查看试题解析