2023-2024学年人教版初中数学八年级下册 20.2 数据的波动程度同步分层训练培优题

试卷更新日期：2024-03-20 类型：同步测试

进入出卷网下载

一、选择题

1. 一组数据1，2，1，4的方差是（）

A、1 B、1.5 C、2 D、2.5

查看试题解析
2. 超市货架上有一批大小不一的鸡蛋，某顾客从中选购了部分大小均匀的鸡蛋设货架上原有鸡蛋质量(单位：g)的平均数和方差分别为 $\bar{x}$ ， S² ，该顾客选购的鸡蛋质量的平均数和方差分别为 $\bar{x_{1}}$ ， $S_{1}^{2}$ ，则下列结论一定成立的是（）

A、 $\bar{x}$ < $\bar{x_{1}}$ B、 $\bar{x}$ > $\bar{x_{1}}$ C、S²> $S_{1}^{2}$ D、S²< $S_{1}^{2}$

查看试题解析
3. 为检测学生体育锻炼效果，从某班随机抽取10名学生进行篮球定时定点投篮检测，投篮进球数统计如图所示，对于这10名学生的定时定点投篮进球数，下列说法错误的是（）

A、中位数是5 B、众数是5 C、平均数是5.2 D、方差是2

查看试题解析
4. 甲、乙、丙、丁四名同学五次数学成绩的平均分与方差如下表所示：

甲
乙
丙
丁
平均数
98
95
98
96
方差
1.2
0.8
0.8
1.0
根据表中的数据，现从中选取一名成绩好且发挥稳定的同学参加学校组织的数学竞赛，应选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
5. 一组数据 $a$ 、 $b$ 、 $c$ 、 $d$ 、 $e$ 、 $f$ 、 $g$ 的平均数是 $m$ ，方差是 $n$ ，则另一组数据 $3 a - 2$ 、 $3 b - 2$ 、 $3 c - 2$ 、 $3 d - 2$ 、 $3 e - 2$ 、 $3 f - 2$ 、 $3 g - 2$ 的平均数和方差分别是（）

A、3， $3 n - 2$ B、 $3 m - 2$ ， $n$ C、 $m - 2$ ， $3 n$ D、 $3 m - 2$ ， $9 n$

查看试题解析
6. 若样本x₁+1，x₂+1，…，x_n+1的平均数为10，方差为2，则对于样本x₁+2，x₂+2，…，x_n+2，下列结论正确的是（）

A、平均数为10，方差为2 B、平均数为11，方差为3 C、平均数为11，方差为2 D、平均数为12，方差为4

查看试题解析
7. 小华进行了5次射击训练后，计算出这5次射击的平均成绩为8环，方差为s₁² ，随后小华又进行了第6次射击，成绩恰好是8环，并计算出这6次射击成绩的方差为s₂² ，则下列说法正确的是（）

A、s₁²=s₂² B、s₁²＜s₂² C、s₁²＞s₂² D、无法确定s₁²与s₂²的大小

查看试题解析
8.
在某次训练中，甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示，对于本次训练，有如下结论：①S_甲²＞S_乙²；②S_甲²＜S_乙²；③甲的射击成绩比乙稳定；④乙的射击成绩比甲稳定，由统计图可知正确的结论是（　　）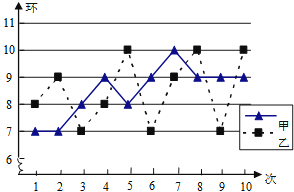

A、①③ B、①④ C、②③ D、②④

查看试题解析

二、填空题

9. 有两个女生小合唱队，各由6名队员组成，甲队与乙队的平均身高均为160 cm，甲队身高方差 $S_{甲}^{2}$ =1.2 cm² ，乙队身高方差 $S_{乙}^{2}$ =2.0 cm² ，两队身高比较整齐的是队（填“甲”或“乙”）.

查看试题解析
10. 已知一组数据x₁，x₂，x₃，…，x。的方差是 1.5，则另一组数据 2x₁，2x₂， 2x₃，…，2x，的方差是.

查看试题解析

11. 甲、乙两班举行一分钟跳绳比赛，参赛学生每分钟跳绳个数的统计结果如表：

班级	参加人数	中位数	方差	平均数
甲	45	109	181	110
乙	45	111	108	110

某同学分析上表后得到如下结论：①甲、乙两班学生平均成绩相同；②乙班优秀人数多于甲班优秀人数(每分钟跳绳≥110个为优秀)；③甲班成绩的波动比乙班大，则正确结论的序号是.

查看试题解析

12. 为迎接体育测试，小强每天坚持引体向上锻炼，他记录了某一周每天做引体向上的个数，如下表：

其中有三天的个数被墨汁覆盖了，但小强已经计算出这组数据唯一的众数是13，平均数是12，那么这组数据的方差是。

查看试题解析
13. 如果一组按从小到大排序的数据a，b，c的平均数是b，方差是S² ，那么数据a+99，b+100，c+101的方差将 S²（填“大于”“小于”或“等于”）.

查看试题解析

三、解答题

14. 甲、乙两名队员参加射击训练，每人射击10次，成绩分别如下：根据以上信息，整理分析数据如下：

	平均成绩/环	中位数/环	众数/环	方差
甲	a	7	7	1.2
乙	7	b	8	c

(1)、

a =

，

b =

，

c =

(2)、填空：（填“甲”或“乙”）.

从中位数的角度来比较，成绩较好的是；从众数的角度来比较，成绩较好的是；成绩相对较稳定的是.

(3)、从甲、乙两名队员中选一名队员参加比赛，选谁更合适，为什么？

查看试题解析

四、综合题

15. 2023年3月5日，中华人民共和国第十四届全国人民代表大会第一次会议在北京召开，某校为使学生更好地了解“两会”，争做新时代好少年，开展了“两会”知识竞赛活动，分别从八（1）班和八（2）班各随机抽取10名学生的竞赛成绩（单位：分，满分100分），并对数据进行了如下分析与整理：
收集数据
八（1）班学生知识竞赛成绩：84，75，82，70，91，83，80，74，79，82
八（2）班学生知识竞赛成绩：80，65，75，68，95，82，84，80，92，79
分析数据

平均数/分
中位数/分
众数/分
方差
八（1）班
80
b
82
31.6
八（2）班
a
80
c
78.4
根据以上信息，解答下列问题：

(1)、填空： $a =$ ， $b =$ ， $c =$ ．

(2)、请你对八（1）班和八（2）班抽取的这10名学生的知识竞赛成绩作出评价．

(3)、该校除开展两会知识竞赛活动外，还组织了制作关于“两会”手抄报的评比活动，并对手抄报进行评分（单位：分，满分100分）．在八（2）班抽取的这10名学生中，甲同学和乙同学的知识竞赛成绩分别为95分和92分，手抄报成绩分别为70分和80分．现对甲同学和乙同学进行综合评分，若知识竞赛成绩占70%，手抄报成绩占30%，则哪位同学的综合成绩较好？

查看试题解析
16. 学校举办纪念“五四运动”104周年暨“青春心向党，建功新时代”演讲比赛．同学们用青春的声音和故事，激扬五四精神，彰显青春风采，展现拼搏风貌，深情地演绎了对党和祖国的热爱之情．

初赛阶段两个年级各10名选手的成绩统计如下：
七年级：98　96　86　85　84　94　77　69　59　94
八年级：99　96　73　82　96　79　65　96　55　96
他们的数据分析过程如下：

(1)、整理、描述数据：根据上面得到的两组数据，分别绘制频数分布直方图如图：

请补全八年级频数分布直方图；

(2)、数据分析：两组数据的平均数、中位数、方差如表所示：
年级
平均数
中位数
方差
七年级
①
85.5
144.36
八年级
83.7
②
251.21
根据以上数据求出表格中①，②两处的数据；

(3)、推断结论：根据以上信息，判断哪个年级比赛成绩整体较好？说明理由（至少从两个不同角度说明判断的合理性）．

查看试题解析

	平均数/分	中位数/分	众数/分	方差
八（1）班	80	b	82	31.6
八（2）班	a	80	c	78.4

年级	平均数	中位数	方差
七年级	①	85.5	144.36
八年级	83.7	②	251.21

	甲	乙	丙	丁
平均数	98	95	98	96
方差	1.2	0.8	0.8	1.0