2023-2024学年人教版初中数学八年级下册 19.3 课题学习选择方案同步分层训练培优题

试卷更新日期：2024-03-20 类型：同步测试

进入出卷网下载

一、选择题

1. 某电信公司推出两种不同的收费标准：A种方式是月租20元；B种方式是月租0元．一个月本地网内打出电话费S（元）与打出时间t（分）的函数图象如图所示，当打出150分钟时，这两种方式的电话费相差（）

A、5元 B、10元 C、15元 D、20元

查看试题解析
2. 在物理实验课上，小宋利用滑轮组及相关器材进行实验，他把得到的拉力 $F (N)$ 和所悬挂物体的重力 $G (N)$ 的几组数据用电脑绘制成如图所示的图象 $($ 不计绳重和摩擦 $)$ ，请你根据图象判断以下结论不正确的是（）

A、施加的拉力 $F$ 随着物体重力 $G$ 的增加而增大 B、当拉力 $F = 2.7 N$ 时，物体的重力 $G = 3.5 N$ C、当物体的重力 $G = 7 N$ 时，拉力 $F = 4.5 N$ D、当滑轮组未悬挂物体在空中静止时，所用拉力为 $1 N$

查看试题解析
3. 声音在空气中传播的速度v（简称声速）与空气温度t的关系（如下表所示），则下列说法错误的是（    ）
温度 $t / ℃$
          $- 15$
          $- 10$
5
10
15
声速 $v / m / s$
321
324
333
336
339

A、在一定范围内，空气温度越高声速越快 B、空气温度每升高 $10 ℃$ ，声速增加 $6 m / s$ C、声速v与温度t之间的关系式为 $v = \frac{3}{5} t + 330$ D、当空气温度为 $20 ℃$ 时，声音 $5 s$ 可以传播 $1740 m$

查看试题解析
4. A、B两地相距12km，甲骑自行车从A地出发前往B地，同时乙步行从B地出发前往A地，如图所示的折线 $O - P - Q$ 和线段EF分别表示甲、乙两人与A地的距离y（km）与时间x（h）之间的函数关系，且OP与EF交于点G．下列说法中错误的是（）

A、甲乙出发后0.5h相遇 B、甲骑自行车的速度为 $18 k m / h$ C、两人相遇地点与A地的距离为9km D、甲、乙相距3km时，出发时间为 $x = \frac{3}{5} h$

查看试题解析
5. $A$ 、 $B$ 两地相距 $80 k m$ ，甲、乙两人沿同一条路从A地到 $B$ 地． $I_{1}$ ， $I_{2}$ 分别表示甲、乙两人离开 $A$ 地的距离 $s$ （ $k m$ ）与时间 $t$ （ $h$ ）之间的关系．对于以下说法：①乙车出发1.5小时后甲才出发；②两人相遇时，他们离开A地 $20 k m$ ；③甲的速度是 $40 k m / h$ ，乙的速度是 $\frac{40}{3} k m / h$ ；④当乙车出发2小时时，两车相距 $13 k m$ ．其中正确的结论有（）

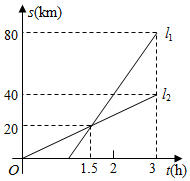A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 在密码学中、直接可以看到的内容称为明码，对明码进行某种处理后得到的内容称为密码．有一种密码，将英文26个字母a，b，c，…，z（不分大小写）依次对应1，2，3，…，26这26个自然数（见表格）．当明码对应的序号x为奇数时，密码对应的序号 $y = \frac{x + 3}{2}$ ；当明码对应的序号x为偶数时，密码对应的序号 $y = \frac{x}{2} + 13$ ．按上述规定，明码和密码相同的序号为（）
字母
a
b
c
d
e
f
g
h
i
j
k
l
m
序号
1
2
3
4
5
6
7
8
9
10
11
12
13
字母
n
o
p
q
r
s
t
u
v
w
x
y
z
序号
14
15
16
17
18
19
20
21
22
23
24
25
26

A、3 B、26 C、3和26 D、1和26

查看试题解析
7. 小泽和小帅分别从甲地骑自行车沿同一条路到乙地．如图是小泽和小帅离甲地的距离y（单位：千米）与时间x（单位：小时）之间函数关系的图象．根据图中信息，下列说法有误的是（）

A、从甲到乙地共24千米 B、小帅的骑车速度为8千米/小时 C、小泽出发0.5小时后小帅才出发 D、当小帅到达乙地时，小泽距乙地还有4千米

查看试题解析
8. 如图，在平面直角坐标系中，▱ABCD各顶点的坐标分别为A（1，-1），B（2，-3），C（4，-3），D（3，-1），若直线y＝-3x+b与▱ABCD有交点，则b的取值范围是（）

A、3≤b≤8 B、2≤b≤8 C、2≤b≤9 D、-3≤b≤9

查看试题解析

二、填空题

9. 如图，点 $B$ ， $C$ 分别在正比例函数 $y = 2 x$ 和一次函数 $y = k x - 2 a (a \neq 0)$ 的图象上， $A$ ， $D$ 为 $x$ 轴上两点，点 $B$ 的纵坐标为 $a$ ．若四边形 $A B C D$ 为矩形，且 $A B = \frac{1}{2} A D$ ，则 $k$ 的值为．

查看试题解析
10. 某市出租车公司规定：出租车收费与行驶路程关系如图所示．如果彤彤乘出租车去学校花了10元，那么彤彤乘车路程有千米．

查看试题解析
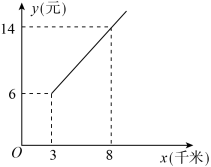11. 如图，甲乙两人以相同的路线前往距离单位 $10 k m$ 的培训中心参加学习，图中 $L_{甲}$ ， $L_{乙}$ 分别表示甲乙两人前往目的地所走的路程S（千米）随时间t（分）变化的函数图象，以下说法：①乙比甲提前 $12$ 分钟到达；②甲、乙相遇时，乙走了6千米；③乙出发6分钟后追上甲．其中正确的是．（填序号）

查看试题解析
12. 如图是本地区一种产品30天的销售图象，图1是产品日销售量y（单位：件）与时间t（单位：天）的函数关系，图2是一件产品的销售利润z（单位，元）与时间t（单位：天）的函数关系，已知日销售利润=日销售量×一件产品的销售利润，下列正确结论的序号是．

①第24天的销售量为200件；

②第10天销售一件产品的利润是15元；

③第12天与第30天这两天的日销售利润相等；

④第30天的日销售利润是750元．

查看试题解析
13. 白鹤公园风景秀丽，成为广大市民休闲锻炼的圣地星期天，小明和爸爸到白鹤公园登山锻炼，他们同时从山脚出发，以各自的速度匀速登山、前20分钟小明以v₁的速度一直在前，由于小明体力不支，休息了20分钟，这时他发现爸已超过他走在了前面，小明立即以v₂的速度追赶爸爸，直到与爸爸相遇，如图是两人之间相距的路程y（米）与爸爸登山时间x（分）之间的函数图象，则 $\frac{v_{1}}{v_{2}}$ ＝.

查看试题解析

三、解答题

14.
我县为了倡导居民节约用水，生活用水按阶梯式水价计费，如图是居民每户每月的水费y(元)与所用的水量x（吨）之间的函数图象，请根据图象所提供的信息，解答下列问题：

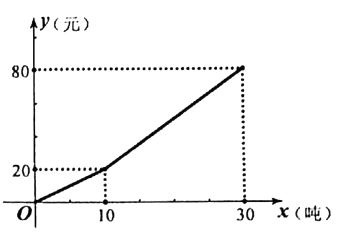(1)、当用水量不超过10吨时，每吨水收费多少元？

(2)、当用水量超过10吨且不超过30吨时，求y与x之间的函数关系式；

(3)、某户居民三、四月份水费共82元，四月份用水比三月份多4吨，求这户居民三月份用水多少吨。

查看试题解析
15.
在平面直角坐标系xOy中，点A（x₁ ， y₁），B（x₂ ， y₂），若x₁x₂+y₁y₂=0，则称A和B互为正交点，即A叫做B的正交点，B也叫做A的正交点。例如：A（1，1），B（2，-2），有1×2+1×（-2）=0，故A和B互为正交点。

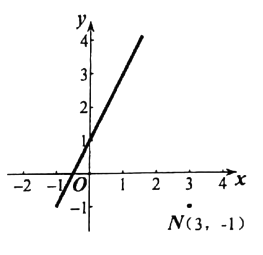(1)、在直角坐标系xOy中，O为坐标原点，判断下列说法是否正确（对的写“正确”，错的写“错误”）。
①原点是任意点的正交点。
②x轴上的任意点与y轴上的任意点都互为正交点。
③点M和N互为正交点，则∠MON=90°.
④点M和N互为正交点，则OM=ON。

(2)、点P和Q互为正交点，P的坐标为（2，-3），Q的坐标为（6，m），求m的值。

(3)、点M是直线y=2x+1上的一点，点M和N（3，-1）互为正交点，求MN的长度。

查看试题解析

四、综合题

16. 如图，在平面直角坐标系中，直线 $l_{1} ： y = - \frac{1}{2} x + 6$ 分别与 $x$ 轴， $y$ 轴交于点 $A$ ，点 $B$ ，与直线 $l_{2} ： y = x$ 交于点 $C$ ．

(1)、求点 $A$ ， $B$ ， $C$ 的坐标；

(2)、若点 $D$ 是线段 $O C$ 上一点，且 $△ B O D$ 的面积是 $△ A O B$ 面积的 $\frac{1}{4}$ ，求直线 $B D$ 的解析式；

(3)、点 $P$ 是直线 $l_{2}$ 上一点，点 $Q$ 是平面内任意一点，若以点 $O$ ， $B$ ， $P$ ， $Q$ 为顶点的四边形是菱形，请直接写出点 $Q$ 的坐标．

查看试题解析
17. 【阅读材料】在“看图说故事”活动中，某学习小组设计了一个问题情境：已知小明家、文具店、体育场依次在同一条直线上，体育场离小明家 $3 k m$ ，文具店离小明家 $2.2 k m$ ，小明从家跑步 $15 m i n$ 到体育场；在那里锻炼了 $30 m i n$ 后，又匀速步行了 $10 m i n$ 到文具店买圆规；在文具店停留了 $10 m i n$ 后，匀速步行 $22 m i n$ 返回家，给出的图象反映了这个过程中小明离开家的距离 $y$ km与小明离开家的时间 $x$ min之间的对应关系．
请根据相关信息，解答下列问题：

(1)、填表：
离开家的时间/min
5
12
30
50
65
离开家的距离/km
1
2.6

(2)、填空：
①体育场到文具店的距离为km；
②小明从文具店返回家的速度为km/min；
③当小明离家的距离为2km时，他离开家的时间为．

(3)、当 $45 \leq x \leq 55$ 时，请直接写出 $y$ 关于 $x$ 的函数解析式．

查看试题解析

温度 $t / ℃$	$- 15$	$- 10$	5	10	15
声速 $v / m / s$	321	324	333	336	339

字母	a	b	c	d	e	f	g	h	i	j	k	l	m
序号	1	2	3	4	5	6	7	8	9	10	11	12	13
字母	n	o	p	q	r	s	t	u	v	w	x	y	z
序号	14	15	16	17	18	19	20	21	22	23	24	25	26

离开家的时间/min	5	12	30	50	65
离开家的距离/km	1			2.6

2023-2024学年人教版初中数学八年级下册 19.3 课题学习 选择方案同步分层训练培优题

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年人教版初中数学八年级下册 19.3 课题学习选择方案同步分层训练培优题