人教版初中数学八年级下册 19.3 课题学习 选择方案同步分层训练基础题
试卷更新日期:2024-03-20 类型:同步测试
一、选择题
-
1. 在弹性限度内,弹簧挂上物体后会伸长,测得弹簧的长度与所挂物体的质量之间有如下关系:
0
1
2
3
4
5
…
10
10.5
11
11.5
12
12.5
…
在弹性限度内,所挂物体的质量为时,弹簧的长度为( )
A、 B、 C、 D、2. 如图,多边形的各顶点都在方格纸的格点(横竖格子线的交错点)上,这样的多边形称为格点多边形,它的面积S可用公式(a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为皮克定理,若有一个格点多边形的面积为9,则b的最大值为( ) A、17 B、18 C、19 D、203. 如图是温度计的示意图,图中左边的温度表示摄氏温度,右边的温度表示华氏温度.小明观察温度计发现,两个刻度x,y之间的关系如下表:
A、17 B、18 C、19 D、203. 如图是温度计的示意图,图中左边的温度表示摄氏温度,右边的温度表示华氏温度.小明观察温度计发现,两个刻度x,y之间的关系如下表:x/℃
10
20
25
30
y/℉
50
68
77
86
据此可知,摄氏温度为15时,对应的华氏温度应为( )
 A、15 B、59 C、-9.4 D、544. 据史书记载,漏刻是中国古代的一种计时工具,是古代人民对函数思想的创造性应用.研究发现水位 h(cm)与时间 t(min) 满足 h=0.4t+2,当 h 为 6cm时,时间 t 的值为( )
A、15 B、59 C、-9.4 D、544. 据史书记载,漏刻是中国古代的一种计时工具,是古代人民对函数思想的创造性应用.研究发现水位 h(cm)与时间 t(min) 满足 h=0.4t+2,当 h 为 6cm时,时间 t 的值为( )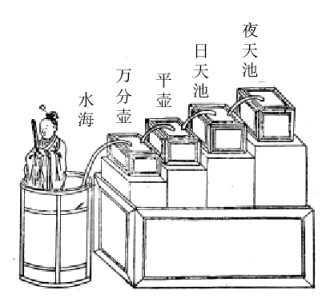 A、4.4min B、10min C、15min D、20min5. 皮克定理是格点几何学中的一个重要定理,它揭示了以格点为顶点的多边形的面积 , 其中分别表示这个多边形内部与边界上的格点个数.在平面直角坐标系中,横、纵坐标都是整数的点为格点.已知 , , 则内部的格点个数是( )A、266 B、270 C、271 D、2856. 如图,若弹簧的总长度是关于所挂重物的一次函数 , 则不挂重物时,弹簧的长度是( )
A、4.4min B、10min C、15min D、20min5. 皮克定理是格点几何学中的一个重要定理,它揭示了以格点为顶点的多边形的面积 , 其中分别表示这个多边形内部与边界上的格点个数.在平面直角坐标系中,横、纵坐标都是整数的点为格点.已知 , , 则内部的格点个数是( )A、266 B、270 C、271 D、2856. 如图,若弹簧的总长度是关于所挂重物的一次函数 , 则不挂重物时,弹簧的长度是( )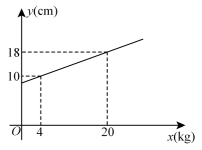 A、 B、 C、 D、7.
A、 B、 C、 D、7.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:
①A,B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③乙车出发后2.5小时追上甲车;
④当甲、乙两车相距50千米时,t=或 .
其中正确的结论有( )
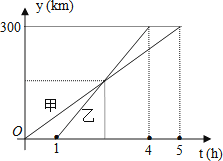 A、1个 B、2个 C、3个 D、4个8. 某生物小组观察一植物生长,得到的植物高度y(单位:厘米)与观察时间x(单位:天)的关系,并画出如图所示的图象(AC是线段,直线CD平行于x轴).下列说法正确的是( ).
A、1个 B、2个 C、3个 D、4个8. 某生物小组观察一植物生长,得到的植物高度y(单位:厘米)与观察时间x(单位:天)的关系,并画出如图所示的图象(AC是线段,直线CD平行于x轴).下列说法正确的是( ).①从开始观察时起,50天后该植物停止长高;
②直线AC的函数表达式为 ;
③第40天,该植物的高度为14厘米;
④该植物最高为15厘米.
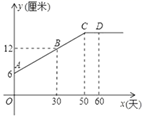 A、①②③ B、②④ C、②③ D、①②③④
A、①②③ B、②④ C、②③ D、①②③④二、填空题
-
9. 和谐号动车刹车后作匀减速运动,速度与刹车时间与之间满足关系式 . 动车在匀变速直线运动中,从开始刹车到准确停到站台,需要 .10. 已知汽车装满油之后,油箱里的剩余油量y(升)与汽车行驶路程x(千米)之间的函数图象如图所示.为了行驶安全,油箱中的油量不能少于(升),那么这辆汽车装满油后至多行驶(千米)后需要再次加油.
 11. 将长为20cm、宽为8cm的长方形白纸按下图所示的方法粘合起来,粘合部分的宽为3cm,设张白纸粘合后的总长度为 , 则关于的函数表达式为.
11. 将长为20cm、宽为8cm的长方形白纸按下图所示的方法粘合起来,粘合部分的宽为3cm,设张白纸粘合后的总长度为 , 则关于的函数表达式为. 12. 甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与行驶时间x(小时)之间的函数关系如图所示,已知甲对应的函数关系式为y=60x , 根据图象提供的信息可知从乙出发后追上甲车需要 小时.
12. 甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与行驶时间x(小时)之间的函数关系如图所示,已知甲对应的函数关系式为y=60x , 根据图象提供的信息可知从乙出发后追上甲车需要 小时. 13.
13.如图,直线y=x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1 , 以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2 , 以原点O为圆心,OB2长为半径画弧交x轴于点A3 , …,按此做法进行下去,点An的坐标为

三、解答题
-
14. 某商场要印制商品宣传材料,甲印刷厂的收费标准是;每份材料收1元印制费,另收1500元制版费;乙印剧厂的收费标准是:每份材料收2.5元印制费,不收制版费.(1)、分别写出两厂的收费y(元)与印制数量x(份)之间的函数表达式.(2)、在同一平面直角坐标系中画出它们的函数图象.(3)、根据函数图象回答下列问题:印制800份宣传材料时,选择哪一家印刷厂比较合算?当花费3000元用于印刷上述宣传材料时,找哪一家印刷厂印制的宣传材料多一些?15. 某食用油的沸点温度远高于水的沸点温度.小聪想用刻度不超过100℃的温度计测算出这种食用油沸点的温度.在老师的指导下,他在锅中倒入一些这种食用油均匀加热,并每隔10s测量一次锅中油温,得到的数据记录如下:
时间 0 10 20 30 40 油温 10 30 50 70 90  (1)、小聪在直角坐标系中描出了表中数据对应的点.经老师介绍,在这种食用油达到沸点前,锅中油温y(℃)与加热的时间t(s)符合初中学习过的某种函数关系,则该函数关系可能是函数关系(选填“正比例”“一次”“二次”“反比例”).(2)、根据以上判断,求y关于t的函数表达式.·(3)、当加热110s时,油沸腾了,请推算沸点的温度.
(1)、小聪在直角坐标系中描出了表中数据对应的点.经老师介绍,在这种食用油达到沸点前,锅中油温y(℃)与加热的时间t(s)符合初中学习过的某种函数关系,则该函数关系可能是函数关系(选填“正比例”“一次”“二次”“反比例”).(2)、根据以上判断,求y关于t的函数表达式.·(3)、当加热110s时,油沸腾了,请推算沸点的温度.四、综合题
-
16. 某校八年级学生外出社会实验活动,为了提前做好准备工作,学校安排小车送义工队前往,同时其余学生乘坐客车去目的地,小车到达目的地后立即返回,客车在目的地等候,如图是两车距学校的距离y(千米)与行驶时间x(小时)之间的函数图象.
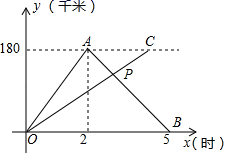 (1)、填空:目的地距离学校千米,小车出发去目的地的行驶速度是千米/时;(2)、当两车行驶3小时后在途中相遇,求点P的坐标;(3)、在第(2)题的条件下,求客车到达目的地所用时间.17. 为提升学生的文学素养,培养学生的阅读兴趣,某校准备购进A,B两种图书.经调查,购进A种图书费用y元与购进A种图书本数x之间的函数关系如图所示,B种图书每本20元.
(1)、填空:目的地距离学校千米,小车出发去目的地的行驶速度是千米/时;(2)、当两车行驶3小时后在途中相遇,求点P的坐标;(3)、在第(2)题的条件下,求客车到达目的地所用时间.17. 为提升学生的文学素养,培养学生的阅读兴趣,某校准备购进A,B两种图书.经调查,购进A种图书费用y元与购进A种图书本数x之间的函数关系如图所示,B种图书每本20元.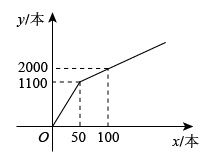 (1)、当和时,求y与x之间的函数关系式;(2)、现学校准备购进300本图书,其中购进A种图书x本,设购进两种图书的总费用为w元.
(1)、当和时,求y与x之间的函数关系式;(2)、现学校准备购进300本图书,其中购进A种图书x本,设购进两种图书的总费用为w元.①当时,求出w与x间的函数表达式;
②若购进A种图书不少于60本,且不超过B种图书本数的2倍,那么应该怎样分配购买A,B两种图书才能使总费用最少?最少总费用多少元?