人教版初中数学八年级下册 19.2.3 一次函数与方程、不等式同步分层训练培优题
试卷更新日期:2024-03-20 类型:同步测试
一、选择题
-
1. 已知方程的解为 , 则一次函数的图像与轴交点的横坐标为( )A、3 B、 C、 D、2. 如图,把直线y=-2x向上平移后得到直线AB,直线AB经过点(m,n),且2m+n=6,则直线AB的解析式是( )
 A、y=-2x-3 B、y=-2x-6 C、y=-2x+3 D、y=-2x+63. 已知二元一次方程组的解为 , 则在同一平面直角坐标系中,直线:与直线:的交点坐标为( )A、 B、 C、 D、4. 如图,在平面直角坐标系xOy中,直线与直线相交于点 , 给出下列结论:
A、y=-2x-3 B、y=-2x-6 C、y=-2x+3 D、y=-2x+63. 已知二元一次方程组的解为 , 则在同一平面直角坐标系中,直线:与直线:的交点坐标为( )A、 B、 C、 D、4. 如图,在平面直角坐标系xOy中,直线与直线相交于点 , 给出下列结论:①;②当时,;③关于x,y的方程组的解是

其中所有正确结论的序号是( )
A、①② B、②③ C、①③ D、①②③5. 如图,在平面直角坐标系中,若直线与直线相交于点 P,则下列结论错误的是( ) A、方程-x+a=bx-4的解是 x=1 B、不等式-x+a<-3和不等式bx-4>-3的解集相同 C、不等式组bx-4<-x+a<0的解集是-2<x<1 D、方程组的解是6. 一次函数的图象与轴、轴形成的三角形的面积为( )A、1 B、2 C、3 D、47. 如图所示,直线y=x+3分别与x轴、y轴交于点A、B,若∠ABC=45°,则直线BC的函数表达式为( )
A、方程-x+a=bx-4的解是 x=1 B、不等式-x+a<-3和不等式bx-4>-3的解集相同 C、不等式组bx-4<-x+a<0的解集是-2<x<1 D、方程组的解是6. 一次函数的图象与轴、轴形成的三角形的面积为( )A、1 B、2 C、3 D、47. 如图所示,直线y=x+3分别与x轴、y轴交于点A、B,若∠ABC=45°,则直线BC的函数表达式为( )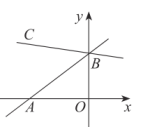 A、y=x+3 B、y=x+3 C、y=x+3 D、y=x+38. 如图,已知点P(6,2),点M , N分别是直线l1:y=x和直线l2:上的动点,连接PM , MN . 则PM+MN的最小值为( )
A、y=x+3 B、y=x+3 C、y=x+3 D、y=x+38. 如图,已知点P(6,2),点M , N分别是直线l1:y=x和直线l2:上的动点,连接PM , MN . 则PM+MN的最小值为( ) A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题
-
9. 如图,直线l₁,l₂相交于点A.观察图象,点A的坐标可以看做方程组的解
 10. 如图,直线(为常数,与x,y轴分别相交于点A,B,则的值是.
10. 如图,直线(为常数,与x,y轴分别相交于点A,B,则的值是. 11. 在同一平面直角坐标系中,直线y=-x+4与y=2x+m相交于点 , 则关于x,y的方程组的解为.12. 在如图所示的平面直角坐标系中,点是直线上的动点, , 是轴上的两点,当取最小值时, .
11. 在同一平面直角坐标系中,直线y=-x+4与y=2x+m相交于点 , 则关于x,y的方程组的解为.12. 在如图所示的平面直角坐标系中,点是直线上的动点, , 是轴上的两点,当取最小值时, .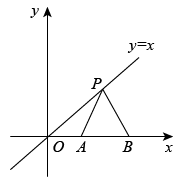 13. 已知直线l的解析式为y=2x+2,菱形AOBA1 , AO1B1A2 , A2O2B2A3 , …按图所示的方式放置,顶点A , A1 , A2 , A3 , …均在直线l上,顶点O , O1 , O2 , …均在x轴上,则点的坐标是 .
13. 已知直线l的解析式为y=2x+2,菱形AOBA1 , AO1B1A2 , A2O2B2A3 , …按图所示的方式放置,顶点A , A1 , A2 , A3 , …均在直线l上,顶点O , O1 , O2 , …均在x轴上,则点的坐标是 .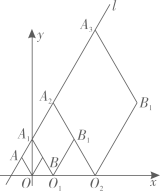
三、解答题
-
14. 如图,在平面直角坐标系中,一次函数的图象分别与轴、轴交于点 , , 点是线段上的一个动点(不与点 , 点重合),过点作轴的垂线交直线于点 , 在射线上取点 , 使.设点的横坐标为.
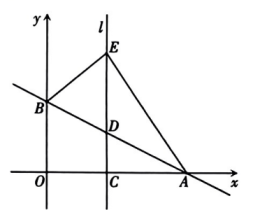 (1)、求 , 两点的坐标;(2)、若点落在直线上,求的值;(3)、请从A,B两题中任选一题作答.我选择 题.
(1)、求 , 两点的坐标;(2)、若点落在直线上,求的值;(3)、请从A,B两题中任选一题作答.我选择 题..若线段的长等于的一半时,求的值.
.若的面积等于面积的一半,求的值.
15. 如图,直线与y轴交于点 , 与x轴交于点 , 直线以每秒1个单位长度的速度沿y轴正方向平移,平移时交线段于点D , 交线段于点C , 当点C与点B重合时结束运动. (1)、求出直线的关系式;(2)、如图1,若直线的函数关系式为 , P是直线上一点,当的面积等于的面积时,求点P的坐标;
(1)、求出直线的关系式;(2)、如图1,若直线的函数关系式为 , P是直线上一点,当的面积等于的面积时,求点P的坐标;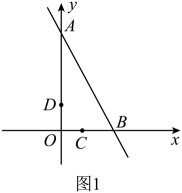 (3)、如图2,在直线运动过程中,过点D作轴交于点E , 连接 , 设运动时间为 . 求出当t为何值时,是等腰三角形?
(3)、如图2,在直线运动过程中,过点D作轴交于点E , 连接 , 设运动时间为 . 求出当t为何值时,是等腰三角形?
四、综合题
-
16. 如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.
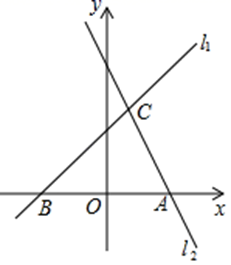 (1)、求直线l2的解析式;(2)、点M在直线l1上,MN∥y轴,交直线l2于点N,若MN=AB,求点M的坐标.(3)、在x轴上是否存在点P,使以B、C、P为顶点的三角形是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.17. 如图,在平面直角坐标系中,点 , 点C在y轴的负半轴上,连接 , 满足 .
(1)、求直线l2的解析式;(2)、点M在直线l1上,MN∥y轴,交直线l2于点N,若MN=AB,求点M的坐标.(3)、在x轴上是否存在点P,使以B、C、P为顶点的三角形是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.17. 如图,在平面直角坐标系中,点 , 点C在y轴的负半轴上,连接 , 满足 . (1)、求直线的解析式;(2)、已知直线经过点B .
(1)、求直线的解析式;(2)、已知直线经过点B .①若点D为直线上一点,若 , 求点D的坐标;
②过点O作直线 , 若点M、N分别是直线和上的点,且满足 . 请问是否存在这样的点 , 使得为直角三角形?若存在,请求出点N的坐标;若不存在,请说明理由.