人教版初中数学八年级下册 19.2.1 正比例函数同步分层训练培优题
试卷更新日期:2024-03-20 类型:同步测试
一、选择题
-
1. 关于正比例函数y=-2x,下列结论正确的是( )A、图象经过点(-1,-2) B、图象经过第一、三象限 C、y随x的增大而减小 D、不论x取何值,总有y<02. 点和都在正比例函数 ( , 且k为常数)的图象上,若 , 则k的值可能是( )A、 B、 C、 D、3. 下列关于正比例函数的结论正确的是( )A、直线经过第一、三象限 B、y随x的增大而减小 C、直线经过点(-1,-2) D、不论x取何值时,总有4. 下列各点中,在正比例函数的图象上的是( )A、 B、 C、 D、5. 正比例函数y=kx的示意图如图所示,则k的值可以是( )
 A、2 B、1 C、0 D、-26. 如图,在平面直角坐标系中,点A1 , A2 , A3 , …,An在x轴上,点B1 , B2 , …,B在直线上,若点A1的坐标为(1,0),且 , , …,都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为S1 , S2 , …,Sn , 则Sn可表示为( )
A、2 B、1 C、0 D、-26. 如图,在平面直角坐标系中,点A1 , A2 , A3 , …,An在x轴上,点B1 , B2 , …,B在直线上,若点A1的坐标为(1,0),且 , , …,都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为S1 , S2 , …,Sn , 则Sn可表示为( )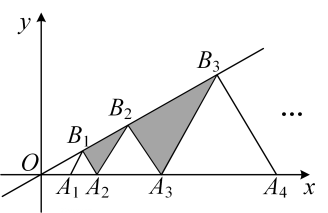 A、 B、 C、 D、7. 如图,直线l1的解析式是y= x,直线l2的解析式是y= x,点A1在l1上,A1的横坐标为 ,作A1B1⊥l1交l2于点B1 , 点B2在l2上,以B1A1、B1B2为邻边在直线l1、l2间作菱形A1B1B2C1 , 延长B2C1交l1于点A2 , 点B3在l2上,以B2A2、B2B3为邻边在l1、l2间作菱形A2B2B3C2 , ………按照此规律继续作下去,则线段A2020B2020长为( )
A、 B、 C、 D、7. 如图,直线l1的解析式是y= x,直线l2的解析式是y= x,点A1在l1上,A1的横坐标为 ,作A1B1⊥l1交l2于点B1 , 点B2在l2上,以B1A1、B1B2为邻边在直线l1、l2间作菱形A1B1B2C1 , 延长B2C1交l1于点A2 , 点B3在l2上,以B2A2、B2B3为邻边在l1、l2间作菱形A2B2B3C2 , ………按照此规律继续作下去,则线段A2020B2020长为( ) A、 B、 C、 D、8. 如图,在平面直角坐标系中,点A在一次函数y= x位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且AB=2 ,AD=1,则OD的最大值是( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,点A在一次函数y= x位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且AB=2 ,AD=1,则OD的最大值是( )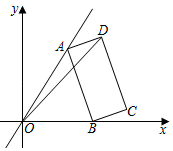 A、 B、 +2 C、 +2 D、
A、 B、 +2 C、 +2 D、二、填空题
-
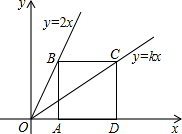
9. 已知正比例函数(k是常数,),y的值随着x的值的增大而增大,请写出一个满足条件的正比例函数的解析式:10. 在正比例函数中,y的值随着x值的增大而增大,则点在第 象限.11. 如图,点B、C分别在两条直线和上,点A、D是轴上两点,已知四边形ABCD是正方形,则k值为.
 12. 已知点A的坐标是 , 点B是正比例函数 的图象上一点,若只存在唯一的点B,使 为等腰三角形,则k的取值范围是.13. 如图,正方形ABCD、正方形A1B1C1D1、正方形A2B2C2D2均位于第一象限内,它们的边平行于x轴或y轴,其中点A、A1、A2在直线OM上,点C、C1、C2在直线ON上,O为坐标原点,已知点A的坐标为(3,3),正方形ABCD的边长为1.若正方形A2B2C2D2的边长为2011,则点B2的坐标为.
12. 已知点A的坐标是 , 点B是正比例函数 的图象上一点,若只存在唯一的点B,使 为等腰三角形,则k的取值范围是.13. 如图,正方形ABCD、正方形A1B1C1D1、正方形A2B2C2D2均位于第一象限内,它们的边平行于x轴或y轴,其中点A、A1、A2在直线OM上,点C、C1、C2在直线ON上,O为坐标原点,已知点A的坐标为(3,3),正方形ABCD的边长为1.若正方形A2B2C2D2的边长为2011,则点B2的坐标为.
三、解答题
-
14. 已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.
(1)求正比例函数的解析式;
(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.
15. 如图,已知正比例函数y=kx经过点A , 点A在第四象限,过点A作AH⊥x轴,垂足为点H , 点A的横坐标为3,且△AOH的面积为3.求正比例函数的表达式.
四、综合题
-
16. 如图,已知为正比例函数的图象上一点,轴,垂足为点B.
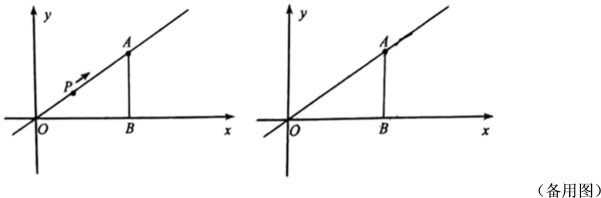 (1)、求m的值;(2)、点P从O出发,以每秒个单位的速度,沿射线方向运动.设运动时间为.
(1)、求m的值;(2)、点P从O出发,以每秒个单位的速度,沿射线方向运动.设运动时间为.①过点P作交直线于点Q,若 , 求t的值;
②在点P的运动过程中,是否存在这样的t,使得为等腰三角形?若存在,请求出所有符合题意的t的值;若不存在,请说明理由.
17. 对于实数x,表示不小于x的最小整数,例如: , , 点为第一象限中的点,将点P分别向上,向下平移个单位得到点 , ;将点P分别向左,向右平移个单位得到点 , , 我们称菱形叫做点P的伴随菱形.例如:点的伴随菱形是以点 , , , 构成的菱形.
 (1)、在图中画出点的伴随菱形,该菱形的面积为 ;
(1)、在图中画出点的伴随菱形,该菱形的面积为 ; (2)、若点的伴随菱形与点的伴随菱形恰有3个公共点,求满足条件的t的最小值;(3)、若点与点所对应的伴随菱形面积相同,且点在函数的图象上,直接写出k的取值范围.
(2)、若点的伴随菱形与点的伴随菱形恰有3个公共点,求满足条件的t的最小值;(3)、若点与点所对应的伴随菱形面积相同,且点在函数的图象上,直接写出k的取值范围.