2023-2024学年人教版初中数学八年级下册 19.2.1 正比例函数同步分层训练提升题

试卷更新日期：2024-03-20 类型：同步测试

进入出卷网下载

一、选择题

1. 已知正比例函数 $y = (k^{2} + 3) x$ 的图象上两点 $A (x_{1} ， y_{1})$ 、 $B (x_{2} ， y_{2})$ ，且 $x_{1} > x_{2}$ ，则下列不等式中一定成立的是（）

A、 $y_{1} + y_{2} > 0$ B、 $y_{1} + y_{2} < 0$ C、 $y_{1} - y_{2} > 0$ D、 $y_{1} - y_{2} < 0$

查看试题解析
2. 正比例函数y=-2x的图象经过的点是（）

A、(1，2) B、(1，-2) C、(-2，1) D、(-2，-1)

查看试题解析
3. 对于函数 $y = - m^{2} x (m$ 是常数， $m \neq 0)$ 的图象，下列说法中不正确的是（）

A、是一条直线 B、过点 $(\frac{1}{m^{2}} ， - 1)$ C、 $y$ 随 $x$ 的减小而增大 D、经过第一、三象限

查看试题解析
4. 若点A（3，-5）和点B（-6，a）都在正比例函数y=kx的图象上，则a的值为（）

A、-10 B、10 C、5 D、-3

查看试题解析
5. 如图，将水以匀速（即单位时间内注入水的体积相同）注入下面圆柱体的容器中，请找出容器内水的高度h和时间t变化关系的图象（）

A、 B、 C、 D、

查看试题解析
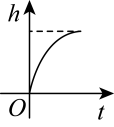6. 已知函数 $y = (k - 3) x$ 是正比例函数，且y随着x的增大而减小，则下面判断正确的是（）

A、 $k > 0$ B、 $k < 0$ C、 $k > 3$ D、 $k < 3$

查看试题解析
7. 如图所示是我国现存最完整的古代计时工具——元代铜壶滴漏，该滴漏从上至下通过多级滴漏，使得上层“壶”中的水可以匀速滴入最下层的圆柱形“壶”中，“壶”中漂浮的带有刻度的木箭随水面匀速缓缓上移，对准标尺就可以读出时辰，如果用 $x$ 表示时间，用 $y$ 表示木箭上升的高度，那么下列图象能表示 $y$ 与 $x$ 的函数关系的是（）

A、 B、 C、 D、

查看试题解析
8. 如图，已知点 $P (6 ， 2)$ ，点M，N分别是直线 $l_{1} ： y = x$ 和直线 $l_{2} ： y = \frac{1}{2} x$ 上的动点，连接 $P M$ ， $M N$ ． $P M + M N$ 的最小值为（）

A、2 B、 $2 \sqrt{5}$ C、 $\sqrt{6}$ D、 $2 \sqrt{3}$

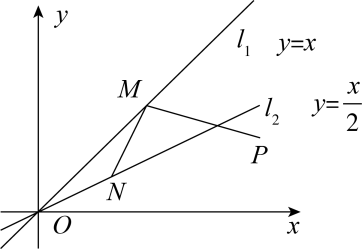查看试题解析

二、填空题

9. 正比例函数y＝kx的图象经过点（1，－2），则k的值是．

查看试题解析
10. 如果直线y＝（2k－3）x经过第二、四象限，则k的取值范围是．

查看试题解析
11. 正比例函数 $y = k x$ 的图象如图所示，则 $k =$ ．

查看试题解析
12. 如图，在平面直角坐标系中，点 $A ， B$ 的坐标分别为 $(n ， 3)$ ， $(3 ， 3)$ ．若直线 $y = 2 x$ 与线段 $A B$ 有公共点，则 $n$ 的值可以为． (写出一个即可)

查看试题解析
13. 函数y=kx(k $\neq$ 0)的图象上有两个点A₁( $x_{1}$ ， $y_{1}$ )，A₂( $x_{2}$ ， $y_{2}$ )，当 $x_{1}$ < $x_{2}$ 时， $y_{1}$ > $y_{2}$ ，写出一个满足条件的函数解析式.

查看试题解析

三、解答题

14. 已知 $y$ 与 $u$ 成正比例， $u$ 与 $x$ 也成正比例，且当 $x = - \frac{1}{2}$ 时， $u = - 3$ ；当 $u = 2$ 时， $y = 1$ .求 $y$ 与 $x$ 之间的函数关系式，并说明它是什么函数.

查看试题解析
15. 已知y+3和2x-1成正比例，且x=2时，y=1。

(1)、写出y与x的函数解析式。

(2)、当0≤x≤3 时，y的最大值和最小值分别是多少？

查看试题解析

四、综合题

16. 已知： $y$ 与 $x + 2$ 成正比例，且当 $x = 1$ 时， $y = - 6$ ．

(1)、求 $y$ 与 $x$ 之间的函数解析式；

(2)、若点 $M (m ， 4)$ 在这个函数的图象上，求 $m$ 的值．

查看试题解析
17. 如图，在平面直角坐标系中，直线y＝kx过点B（m，6），过点B分别作x轴和y轴的垂线，垂足分别为点A，C，∠AOB＝30°.动点P从点O出发，以每秒2个单位长度的速度向点B运动，动点Q从点B出发.以每秒 $\sqrt{3}$ 个单位长度的速度向点C运动.点P，Q同时开始运动，当点P到达点B时，点P，Q同时停止运动，设运动时间为t秒.

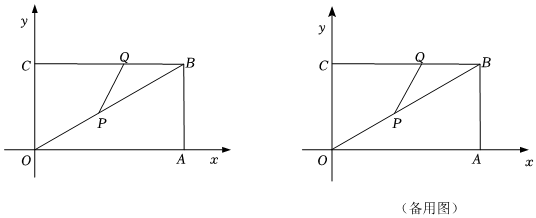(1)、求m与k的值；

(2)、设△PQB的面积为S，求S与t的关系式；

(3)、若以点P，Q，B为顶点的三角形是等腰三角形，请求出t的值.（温擎提示：在直角三角形中，30°的角所对的直角边等于斜边的一半）

查看试题解析