2023-2024学年人教版初中数学八年级下册 18.2.3 正方形同步分层训练提升题

试卷更新日期：2024-03-20 类型：同步测试

进入出卷网下载

一、选择题

1. 下列说法正确的是（）

A、对角线互相垂直的平行四边形是正方形 B、一组对边平行另一组对边相等的四边形是平行四边形 C、一组对边平行另一组对角相等的四边形是平行四边形 D、对角线互相垂直的四边形是菱形

查看试题解析
2. 如图，在正方形ABCD的外侧，作等边三角形DCE，连接AE，则∠ADE为（）

A、120° B、130° C、150° D、160°

查看试题解析
3. 下列说法错误的是（）

A、平行四边形的对边相等 B、正方形的对角线互相垂直平分且相等 C、菱形的对角线相等且平分 D、矩形的对角线相等且互相平分

查看试题解析
4. 如图一标志性建筑的底面呈正方形，底面采用4块完全相同的长方形地砖和一块正方形地砖拼成，则以下说法正确的是 $($ $)$

A、由长方形地砖的周长可求外面大正方形的面积 B、由长方形地砖的面积可求外面大正方形的面积 C、由里面小正方形地砖的周长可求长方形的面积 D、由里面小正方形地砖的面积可求大正方形的面积

查看试题解析
5. 在图1所示的 $3 \times 3$ 的网格内有一个八边形，其中每个小方格的边长均为1.经探究发现，此八边形可按图2的方式分割成四个全等的五边形和一个小正方形①.现将分割后的四个五边形重新拼接(即图2中的阴影部分)，得到一个大正方形ABCD，发现该正方形中间的空白部分②也是个正方形，记正方形①得面积为S₁ ，正方形②的面积为S₂ ，且 $S_{1} ： S_{2} = 3 ： 2$ ，则大正方形ABCD的边长为（）

A、 $\sqrt{3}$ B、2 C、 $\sqrt{5}$ D、 $\sqrt{6}$

查看试题解析
6. 如图，点E是正方形ABCD内部的一点，△CDE为等边三角形，连接AE并延长交BD于点F，∠AFD的度数为（）

A、55° B、60° C、70° D、75°

查看试题解析
7. 如图，用两个边长为1的小正方形拼成一个大正方形，则下列关于大正方形边长 $a$ 的说法正确的是（）

A、 $a$ 是整数 B、 $a$ 满足 $a^{2} = 4$ C、 $a$ 是分数 D、 $a$ 是无理数

查看试题解析
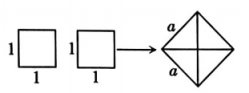8. 我们知道，四边形具有不稳定性，如图，在平面直角坐标系中，边长为2的正方形 $A B C D$ 的边 $A B$ 在x轴上， $A B$ 的中点是坐标原点O，固定点A，B，把正方形沿箭头方向推，使点D落在y轴正半轴上点 $D^{'}$ 处，则点C的对应点 $C^{'}$ 的坐标为（）

A、 $(\sqrt{3} ， 1)$ B、 $(2 ， 1)$ C、 $(1 ， \sqrt{3})$ D、 $(2 ， \sqrt{3})$

查看试题解析

二、填空题

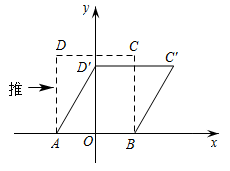9. 如图， $∠ A E D = 90 °$ ，正方形 $A B C D$ 和正方形 $A E F G$ 的面积分别是169和144，则以 $D E$ 为直径的半圆的面积是．

查看试题解析
10. 如图，在坐标系中，正方形 $O A B C$ 的边长为2，点 $P$ 是 $x$ 轴上一动点．若 $B P$ 与 $∠ A B C$ 的两边所组成的角的度数之比为 $1 ： 3$ ，则点 $P$ 的坐标为．

查看试题解析
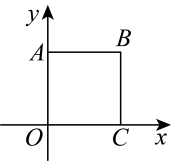11. 我们知道，在图形从一般向特殊变化的过程中，它的组成元素及相关元素之间的关系也越来越特殊.下面是小颖从“对角线”的角度对平行四边形矩形、菱形、正方形之间关系的梳理，图中“▲”处应填写的内容是.

查看试题解析
12. 如图，直线 $l$ 过正方形 $A B C D$ 的顶点 $B$ ，点 $A$ ， $C$ 到直线 $l$ 的距离 $A E$ ， $C F$ 分别为6和4，则正方形 $A B C D$ 的面积是。

查看试题解析
13. 如图，将正方形 $O A B C$ 放在平面直角坐标系中， $O$ 是坐标原点， $A$ 的坐标为 $(3 ， 4)$ ，则点 $B$ 的坐标为.

查看试题解析

三、解答题

14. 如图所示，直线a经过正方形ABCD的顶点A，分别过正方形ABCD的顶点B，D作BF⊥a于点F，DE⊥a于点E，若DE=8，BF=5，求EF的长．

查看试题解析
15. 如图，在矩形ABCD中，M、N分别是AD、BC的中点，P、Q分别是BM、DN的中点.

(1)、求证： $B M = D N$ .

(2)、连接MQ、PN ，判断四边形MPNQ的形状，并说明理由.

(3)、矩形ABCD的边AB与AD满足什么长度关系时，四边形MPNQ是正方形？请说明理由.

查看试题解析

四、综合题

16. 已知：如图，在菱形ABCD中，点E，O，F分别为AB，AC，AD的中点，连接CE，CF，OE，OF．

(1)、求证：△BCE≌△DCF；

(2)、当AB与BC满足什么关系时，四边形AEOF是正方形？请说明理由．

查看试题解析
17. 如图 $1$ ，正方形 $A B C D$ 的边长为 $a$ ， $E$ 为边 $C D$ 上一动点 $($ 点 $E$ 与点 $C$ ， $D$ 不重合 $)$ ，连接 $A E$ 交对角线 $B D$ 于点 $P$ ，过点 $P$ 作 $P F ⊥ A E$ 交 $B C$ 于点 $F$ ，连接 $P C$ ．

(1)、求证： $P A = P C$ ；

(2)、如图 $2$ ，过点 $F$ 作 $F O ⊥ B D$ 于 $Q$ ，在点 $E$ 的运动过程中， $P Q$ 的长度是否发生变化？若不变，求出 $P Q$ 的长；若变化，请说明变化规律．

(3)、证明：在点 $E$ 的运动过程中，总有 $A B + B F = \sqrt{2} B P$ 成立．

查看试题解析