人教版初中数学八年级下册 18.2.3 正方形同步分层训练基础题
试卷更新日期:2024-03-20 类型:同步测试
一、选择题
-
1. 下列说法中正确的是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是正方形 C、平行四边形的对角线平分一组对角 D、矩形的对角线相等且互相平分2. 如图,是正方形的边延长线上的一点,且交于点 , 则的度数为( )
 A、 B、 C、 D、3. 下列命题中,假命题是( )A、平行四边形的对角线互相垂直平分 B、矩形的对角线相等 C、菱形的面积等于两条对角线乘积的一半 D、对角线相等的菱形是正方形4. 如图,延长正方形ABCD的一边BC到E,使CE=AC,连接AE交CD于F,则∠AFC的度数是( )
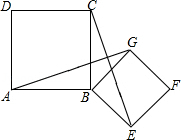
A、 B、 C、 D、3. 下列命题中,假命题是( )A、平行四边形的对角线互相垂直平分 B、矩形的对角线相等 C、菱形的面积等于两条对角线乘积的一半 D、对角线相等的菱形是正方形4. 如图,延长正方形ABCD的一边BC到E,使CE=AC,连接AE交CD于F,则∠AFC的度数是( ) A、 B、 C、 D、5. 如图,在Rt中,4,点是斜边BC的中点,以AM为边作正方形AMEF.若S正方形AMEF=16,则( )
A、 B、 C、 D、5. 如图,在Rt中,4,点是斜边BC的中点,以AM为边作正方形AMEF.若S正方形AMEF=16,则( ) A、 B、 C、12 D、166. 如图,在正方形ABCD中, , , 且 , 则BE的长为( )
A、 B、 C、12 D、166. 如图,在正方形ABCD中, , , 且 , 则BE的长为( ) A、 B、 C、 D、7. 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 ( )
A、 B、 C、 D、7. 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 ( ) A、2.5 B、 C、 D、28. 如图,在正方形OABC中,O是坐标原点,点A的坐标为(1,),则点C的坐标是( )
A、2.5 B、 C、 D、28. 如图,在正方形OABC中,O是坐标原点,点A的坐标为(1,),则点C的坐标是( ) A、(﹣ , 1) B、(﹣1,) C、(﹣ , 1) D、(﹣ , ﹣1)
A、(﹣ , 1) B、(﹣1,) C、(﹣ , 1) D、(﹣ , ﹣1)二、填空题
-
9. 如图,A(0,2),D(1,0),以AD为边作正方形ABCD , 则点B的坐标为 .
 10. 如图,四边形是菱形,对角线与相交于点O,请添加条件 , 使得菱形为正方形.(只能添加一个条件)
10. 如图,四边形是菱形,对角线与相交于点O,请添加条件 , 使得菱形为正方形.(只能添加一个条件) 11. 小颖将能够活动的菱形学具活动成为图1所示形状,并测得 , .接着,她又将这个学其活动成为图2所示正方形,此时的长为.
11. 小颖将能够活动的菱形学具活动成为图1所示形状,并测得 , .接着,她又将这个学其活动成为图2所示正方形,此时的长为.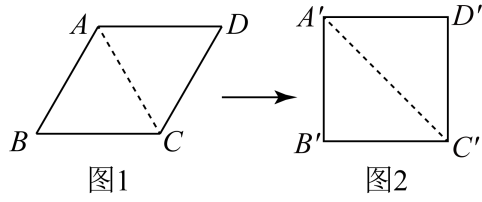 12. 七巧板是我国民间广为流传的一种益智玩具.某同学用边长为4dm的正方形纸板制作了一副七巧板(见图),由5个等腰直角三角形,1个正方形和1个平行四边形组成.则图中阴影部分的面积为dm2.
12. 七巧板是我国民间广为流传的一种益智玩具.某同学用边长为4dm的正方形纸板制作了一副七巧板(见图),由5个等腰直角三角形,1个正方形和1个平行四边形组成.则图中阴影部分的面积为dm2. 13. 如图,点P是正方形ABCD内位于对角线AC下方的一点,若 , 则的度数为.
13. 如图,点P是正方形ABCD内位于对角线AC下方的一点,若 , 则的度数为.
三、解答题
-
14.
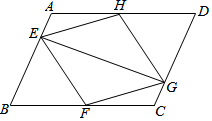
 (1)、如图①,在正方形ABCD中,E为边CD上一点,连结AE,过点A作AF⊥AE交CB的延长线于点F,猜想AE与AF的数量关系,并说明理由;(2)、如图②,在(1)的条件下,连结AC,过点A作AM⊥AC交CB的延长线于点M ,观察并猜想CE与MF的数量关系,并说明理由.15. 如图,在正方形ABCD中,点E,F分别在BC,CD上移动,且A到EF的距离AH始终保持与AB长相等,问在E,F移动过程中;
(1)、如图①,在正方形ABCD中,E为边CD上一点,连结AE,过点A作AF⊥AE交CB的延长线于点F,猜想AE与AF的数量关系,并说明理由;(2)、如图②,在(1)的条件下,连结AC,过点A作AM⊥AC交CB的延长线于点M ,观察并猜想CE与MF的数量关系,并说明理由.15. 如图,在正方形ABCD中,点E,F分别在BC,CD上移动,且A到EF的距离AH始终保持与AB长相等,问在E,F移动过程中; (1)、∠EAF的大小是否有变化?请说明理由.(2)、△ECF的周长是否有变化?请说明理由.
(1)、∠EAF的大小是否有变化?请说明理由.(2)、△ECF的周长是否有变化?请说明理由.四、综合题