人教版初中数学八年级下册 18.2.2 菱形同步分层训练提升题
试卷更新日期:2024-03-20 类型:同步测试
一、选择题
-
1. 顺次连接矩形各边中点得到的四边形是( )A、梯形 B、矩形 C、菱形 D、正方形2. 菱形不一定具有的性质是( )A、四条边相等 B、对角线相等 C、是轴对称图形 D、是中心对称图形3. 一个菱形的边长为 ,面积为 ,则该菱形的两条对角线的长度之和为( )A、 B、 C、 D、4. 如图,在菱形 ABCD中,对角线AC,BD相交于点O,下列说法错误的是 ( )
 A、AB∥DC B、∠DAO=∠DCO C、AC⊥BD D、OA=BD5. 如图,菱形ABCD中,点О为对称中心,点E从点A出发沿AB向点B移动,移动到点B停止.作射线EO,交边CD于点F,则四边形AECF形状的变化依次为( )
A、AB∥DC B、∠DAO=∠DCO C、AC⊥BD D、OA=BD5. 如图,菱形ABCD中,点О为对称中心,点E从点A出发沿AB向点B移动,移动到点B停止.作射线EO,交边CD于点F,则四边形AECF形状的变化依次为( )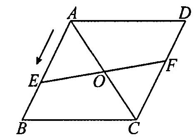 A、平行四边形→正方形→平行四边形→矩形 B、平行四边形→矩形→平行四边形→菱形 C、平行四边形→正方形→菱形→矩形 D、平行四边形→菱形→正方形→矩形6. 如图,直线 , 菱形ABCD和等边在之间,点A,F分别在上,点B,D,E,G在同一直线上.若 , 则( )
A、平行四边形→正方形→平行四边形→矩形 B、平行四边形→矩形→平行四边形→菱形 C、平行四边形→正方形→菱形→矩形 D、平行四边形→菱形→正方形→矩形6. 如图,直线 , 菱形ABCD和等边在之间,点A,F分别在上,点B,D,E,G在同一直线上.若 , 则( )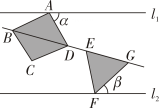 A、 B、 C、 D、7. 如图,在菱形中,是的中点, , 交于点 , 如果 , 那么菱形的周长为( )
A、 B、 C、 D、7. 如图,在菱形中,是的中点, , 交于点 , 如果 , 那么菱形的周长为( )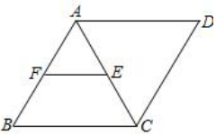 A、12 B、20 C、24 D、228. 如图,菱形中, , 与交于点 , 为延长线上的一点,且 , 连接分别交 , 于点、 , 连接 , 则下列结论:( )
A、12 B、20 C、24 D、228. 如图,菱形中, , 与交于点 , 为延长线上的一点,且 , 连接分别交 , 于点、 , 连接 , 则下列结论:( )
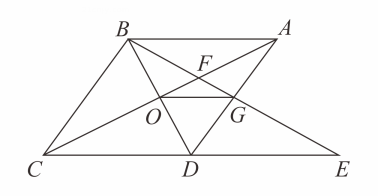
;与全等的三角形共有个;
;由点、、、构成的四边形是菱形.
A、 B、 C、 D、二、填空题
-
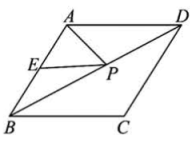
9. 菱形的两条对角线长分别为和 , 则这个菱形的周长为 .10. 若菱形的两条对角线长分别为6和8,则该菱形的面积为 .11. 如图,在菱形ABCD中, , 点E为AB中点,点P在对角线BD上运动,若 , 则AB长的最大值为.
 12. 如图,若菱形的面积为 , , 将菱形折叠,使点恰好落在菱形对角线的交点处,折痕为 , 则cm.
12. 如图,若菱形的面积为 , , 将菱形折叠,使点恰好落在菱形对角线的交点处,折痕为 , 则cm.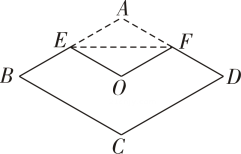 13. 如图,在菱形ABCD中,对角线AC,BD相交于点O,点E在线段BO上,连接AE,若CD=2BE, , 则线段AE的长为 .
13. 如图,在菱形ABCD中,对角线AC,BD相交于点O,点E在线段BO上,连接AE,若CD=2BE, , 则线段AE的长为 .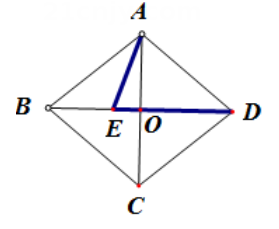
三、解答题
-
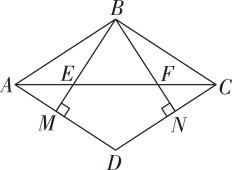
14. 如图,在菱形 ABCD 中,过点 B 作 BM⊥AD 于点 M,BN⊥CD 于点 N,BM,BN 分别交AC 于点 E,F.求证:AE=CF.
 15. 如图,四边形 ABCD 是菱形,对角线 AC,BD 相交于点O,AB=2,AC=2.求:
15. 如图,四边形 ABCD 是菱形,对角线 AC,BD 相交于点O,AB=2,AC=2.求: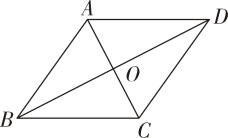 (1)、菱形 ABCD的周长.(2)、BD的长.(3)、菱形 ABCD的面积.
(1)、菱形 ABCD的周长.(2)、BD的长.(3)、菱形 ABCD的面积.四、综合题