2023-2024学年人教版初中数学八年级下册 18.2.2 菱形同步分层训练基础题
试卷更新日期：2024-03-20 类型：同步测试
一、选择题
-
1. 菱形的对角线 ， 则菱形的面积是（ ）A、20 B、15 C、12 D、102. 如图，菱形的周长为8，是的中点， ， 交于点 ， 那么的长是（ ）
A、4 B、3 C、2 D、13. 在下列条件中，能够判定四边形是菱形的是（ ）A、两条对角线相等 B、两条对角线相等且互相垂直 C、两条对角线互相垂直 D、两条对角线互相垂直平分4. 如图，为菱形的对角线，若 ， 则的度数为（ ）
A、 B、 C、 D、5. 如图，菱形ABCD的两条对角线交于点O，BE⊥DC，交DC的延长线于点E，若AC=6， BD=8，则BE的长是（ ）
A、 B、 C、 D、46. 如图，将△ABC沿BC方向平移得到△DCE，连结BD，AD，下列条件不能判定四边形ABCD是菱形的是（ ）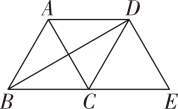
A、∠ABC=∠ACB B、AB=AD C、∠BAC=∠DAC D、AC⊥BD7. 如图，在菱形 ABCD中，对角线 AC，BD相交于点O，E 是边AD的中点，连结OE.若菱形ABCD的周长为32，则 OE 的长为 （ ）
A、4 B、6 C、8 D、128. 如图，菱形 ABCD的对角线AC，BD相交于点O.若AC=6，BD=8，AE⊥BC，垂足为 E，则AE 的长为 （ ）
A、 B、 C、 D、10二、填空题
-
9. 如右图，把一个长方形的纸片对折两次，然后剪下一个角，为了得到一个锐角为60°的菱形，剪口与折痕所成的角α的度数应为.
10. 如图，连接四边形ABCD各边中点，得到四边形EFGH ， 只要添加条件ACBD ． 就能保证四边形EFGH是菱形．
11. 如图，将两条宽度均为2的纸条相交成30°的角叠放，则重合部分构成的四边形ABCD的面积为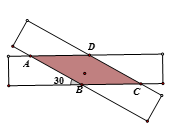
12. 如图，四边形ABCD是菱形，O是两条对角线的交点，过点O的三条直线将菱形分成阴影部分和空白部分.当菱形的两条对角线的长分别为6和8时，阴影部分的面积为.
13. 如图，菱形 ABCD的边AB 的垂直平分线交AB 于点 E，交 AC 于 点 F，连 结 DF. 若∠BAD=100°，则∠CDF=°.
三、解答题
-
14. 如图，菱形ABCD的对角线相交于点O，BE∥AC，AE∥BD，EO与AB相交于点F．
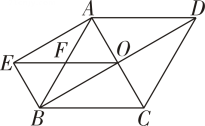(1)、求证：EO=DC；(2)、若菱形ABCD的边长为10，∠EBA=60°，求菱形ABCD的面积．15. 小惠自编一题：“如图，在四边形ABCD中，对角线AC，BD相交于点O，AC⊥BD，OB=OD．求证：四边形ABCD是菱形”，并将自己的证明过程与同学小洁交流．小惠：
证明：∵AC⊥BD，OB=OD，
∴AC垂直平分BD，
∴AB=AD，CB=CD，
∴四边形ABCD是菱形．
小洁：
这个题目还缺少条件，需要补充一个条件才能证明．
若赞同小惠的证法，请在第一个方框“”内打“√" ；若赞成小洁的说法，请你补充一个条件，并证明．四、综合题
