人教版初中数学八年级下册 18.2.1 矩形同步分层训练培优题
试卷更新日期:2024-03-20 类型:同步测试
一、选择题
-
1. 已知四边形ABCD中,∠A=∠B=∠C=90°,对角线AC,BD相交于点O.下列结论一定成立的是( )A、AC⊥BD B、AC=BD C、AB=BC D、AB=AC2. 如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AC=6,则矩形的边AB的长为( )
 A、3 B、6 C、 D、3. 如图,在矩形ABCD中,对角线AC、BD交于点O,已知OA=5, , 则下列选项中图形的周长是有理数的是( )
A、3 B、6 C、 D、3. 如图,在矩形ABCD中,对角线AC、BD交于点O,已知OA=5, , 则下列选项中图形的周长是有理数的是( )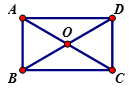 A、 B、 C、 D、矩形4. 如图,在中, , 是高,是中线,那么在结论① , ② , ③ , ④ , ⑤中错误的个数( )
A、 B、 C、 D、矩形4. 如图,在中, , 是高,是中线,那么在结论① , ② , ③ , ④ , ⑤中错误的个数( ) A、1个 B、2个 C、3个 D、4个5. 如图,在中,是上的一点, , 分别是 , 的中点, , 则的长是( )
A、1个 B、2个 C、3个 D、4个5. 如图,在中,是上的一点, , 分别是 , 的中点, , 则的长是( ) A、3 B、4 C、5 D、66. 如图,四边形OABC是矩形,A(2,1),B(0,5),点C在第二象限,则点C的坐标是( )
A、3 B、4 C、5 D、66. 如图,四边形OABC是矩形,A(2,1),B(0,5),点C在第二象限,则点C的坐标是( ) A、(-1,3) B、(-1,2) C、(-2,3) D、(-2,4)7. 如图,在矩形ABCD中,AC,BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,OA=6,则BE的长为( )
A、(-1,3) B、(-1,2) C、(-2,3) D、(-2,4)7. 如图,在矩形ABCD中,AC,BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,OA=6,则BE的长为( ) A、5 B、6 C、7 D、88. 如图,四边形ABCD是矩形, , , 点P是边AD上一点不与点A , D重合 , 连接PB , PC , 点M , N分别是PB , PC的中点,连接MN , AM , DN , 点E在边AD上, , 则的最小值是( )
A、5 B、6 C、7 D、88. 如图,四边形ABCD是矩形, , , 点P是边AD上一点不与点A , D重合 , 连接PB , PC , 点M , N分别是PB , PC的中点,连接MN , AM , DN , 点E在边AD上, , 则的最小值是( ) A、 B、3 C、 D、
A、 B、3 C、 D、二、填空题
-
9. 如图是一块长方形ABCD的场地,长AB=a米,宽AD=b米,从A、B两处入口的小路宽都为1米,两小路汇合处路宽为2米,其余部分种植草坪,则草坪面积为 .
 10. 数学家笛卡尔在《几何》一书中阐述了坐标几何思想,主张取代数和几何中最好的东西以长补短.如图,在直角坐标系中,有一矩形 , 点的坐标是 , 则的长是。
10. 数学家笛卡尔在《几何》一书中阐述了坐标几何思想,主张取代数和几何中最好的东西以长补短.如图,在直角坐标系中,有一矩形 , 点的坐标是 , 则的长是。 11. 如图,矩形的顶点在轴上,点的坐标为 , 固定边 , 向左“推”矩形使点落在轴的点的位置,则点的对应点的坐标是 .
11. 如图,矩形的顶点在轴上,点的坐标为 , 固定边 , 向左“推”矩形使点落在轴的点的位置,则点的对应点的坐标是 . 12. 如图,在矩形ABMN中,AN=1,点C是MN的中点,分别连接AC,BC,且BC=2,点D为AC的中点,点E为边AB上一个动点,连接DE,点A关于直线DE的对称点为点F,分别连接DF,EF.当EF⊥AC时,AE的长为.
12. 如图,在矩形ABMN中,AN=1,点C是MN的中点,分别连接AC,BC,且BC=2,点D为AC的中点,点E为边AB上一个动点,连接DE,点A关于直线DE的对称点为点F,分别连接DF,EF.当EF⊥AC时,AE的长为.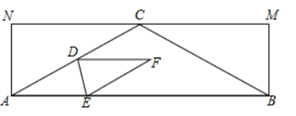 13. 如图,将矩形ABCD沿着GE、EC、GF翻折,使得点A、B、D恰好都落在点O处,且点G、O、C在同一条直线上,同时点E、O、F在另一条直线上,则的值是 .
13. 如图,将矩形ABCD沿着GE、EC、GF翻折,使得点A、B、D恰好都落在点O处,且点G、O、C在同一条直线上,同时点E、O、F在另一条直线上,则的值是 .
三、解答题
-
14. 如图,在四边形ABCD中,∠BAD=∠BCD= 90°,BC=6,CD=AC=8,M,N分别是对角线BD,AC的中点,连结AM.
 (1)、求AM的长.(2)、求证:MN⊥AC.(3)、求MN的长.15. 巴台农神庙的设计代表了古希腊建筑艺术上的最高水平,它的平面图可看作宽与长的比是的矩形,我们将这种宽与长的比是的矩形叫黄金矩形.如图①,已知黄金矩形的宽 .
(1)、求AM的长.(2)、求证:MN⊥AC.(3)、求MN的长.15. 巴台农神庙的设计代表了古希腊建筑艺术上的最高水平,它的平面图可看作宽与长的比是的矩形,我们将这种宽与长的比是的矩形叫黄金矩形.如图①,已知黄金矩形的宽 .
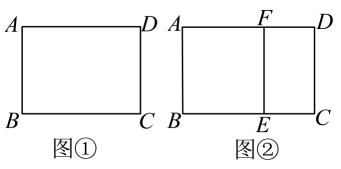 (1)、黄金矩形的长 ;(2)、如图②,将图①中的黄金矩形裁剪掉一个以为边的正方形 , 得到新的矩形 , 猜想矩形是否为黄金矩形,并证明你的结论;(3)、在图②中,连接 , 求点到线段的距离.
(1)、黄金矩形的长 ;(2)、如图②,将图①中的黄金矩形裁剪掉一个以为边的正方形 , 得到新的矩形 , 猜想矩形是否为黄金矩形,并证明你的结论;(3)、在图②中,连接 , 求点到线段的距离.四、综合题
-
16. 已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.
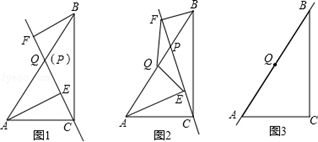 (1)、如图1,当点P与点Q重合时,AE与BF的位置关系是 , QE与QF的数量关系式;(2)、如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;(3)、如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.17. 如图①,在四边形ABCD中, , , , , , 点P从点A出发,沿射线AD以每秒2个单位长度的速度运动,点Q从点C出发,沿CB方向以每秒1个单位长度的速度向终点B运动,P、Q两点同时出发,当点Q到达点B时,点P也随之停止运动,设点Q运动时间为t秒.
(1)、如图1,当点P与点Q重合时,AE与BF的位置关系是 , QE与QF的数量关系式;(2)、如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;(3)、如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.17. 如图①,在四边形ABCD中, , , , , , 点P从点A出发,沿射线AD以每秒2个单位长度的速度运动,点Q从点C出发,沿CB方向以每秒1个单位长度的速度向终点B运动,P、Q两点同时出发,当点Q到达点B时,点P也随之停止运动,设点Q运动时间为t秒. (1)、AB的长为 .(2)、求线段PD的长(用含t的代数式表示).(3)、当以P、D、C、Q为顶点的四边形为平行四边形时,求t的值.(4)、如图②,若点E为BC边上一点,且 , 当是以BE为腰的等腰三角形时,直接写出t的值.
(1)、AB的长为 .(2)、求线段PD的长(用含t的代数式表示).(3)、当以P、D、C、Q为顶点的四边形为平行四边形时,求t的值.(4)、如图②,若点E为BC边上一点,且 , 当是以BE为腰的等腰三角形时,直接写出t的值.