人教版初中数学八年级下册 18.1.2 平行四边形的判定同步分层训练基础题
试卷更新日期:2024-03-20 类型:同步测试
一、选择题
-
1. 如图,在△ABC中,D , E分别是边AB , AC的中点,若DE=6,则BC=( )
 A、18 B、12 C、10 D、82. 如图,任意四边形各边中点分别是、、、若对角线、的长分别是、 , 则四边形的周长是( )
A、18 B、12 C、10 D、82. 如图,任意四边形各边中点分别是、、、若对角线、的长分别是、 , 则四边形的周长是( ) A、 B、 C、 D、3. 如图, , 两地被池塘隔开,小明在外选一点 , 连接 , , 分别取 , 的中点 , , 为了测量 , 两地间的距离,则可以选择测量以下线段中哪一条的长度( )
A、 B、 C、 D、3. 如图, , 两地被池塘隔开,小明在外选一点 , 连接 , , 分别取 , 的中点 , , 为了测量 , 两地间的距离,则可以选择测量以下线段中哪一条的长度( )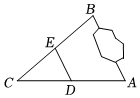 A、 B、 C、 D、4. 如图,为估计池塘两岸边A , B两点间的距离,在池塘的一侧选取点C , 分别取AC , BC的中点D , E , 测得DE=15m,则A , B两点间的距离是( )
A、 B、 C、 D、4. 如图,为估计池塘两岸边A , B两点间的距离,在池塘的一侧选取点C , 分别取AC , BC的中点D , E , 测得DE=15m,则A , B两点间的距离是( )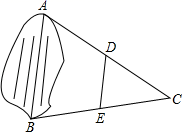 A、15m B、20m C、30m D、60m5. 如图,在四边形ABCD中,E是BC边的中点,连结DE并延长,交AB的延长线于F点,AB=BF.添加个条件,使四边形ABCD是平行四边形.你认为下面四个条件中可选择的是( )
A、15m B、20m C、30m D、60m5. 如图,在四边形ABCD中,E是BC边的中点,连结DE并延长,交AB的延长线于F点,AB=BF.添加个条件,使四边形ABCD是平行四边形.你认为下面四个条件中可选择的是( ) A、AD=BC B、CD=BF C、∠A=∠C D、∠F=∠CDE6. 如图,在平行四边形ABCD中,E为BC上一点,连结AE,AC.已知AE=CE,AB=BE,记∠ACB=α,则用α的代数式表示∠ACD的度数为( )
A、AD=BC B、CD=BF C、∠A=∠C D、∠F=∠CDE6. 如图,在平行四边形ABCD中,E为BC上一点,连结AE,AC.已知AE=CE,AB=BE,记∠ACB=α,则用α的代数式表示∠ACD的度数为( ) A、2α B、90°-2α C、3α D、180°-4a7. 如图,平行四边形ABCD的对角线AC、BD相交于点O,OE∥AB交AD于点E.若OA=2,△AOE的周长为10,则平行四边形ABCD的周长为( )
A、2α B、90°-2α C、3α D、180°-4a7. 如图,平行四边形ABCD的对角线AC、BD相交于点O,OE∥AB交AD于点E.若OA=2,△AOE的周长为10,则平行四边形ABCD的周长为( ) A、16 B、32 C、36 D、408. 如图,在平行四边形中, , , , , 分别是边 , 上的动点,连接 , , , 分别是 , 的中点,连接 , 则的最大值与最小值的差为( )
A、16 B、32 C、36 D、408. 如图,在平行四边形中, , , , , 分别是边 , 上的动点,连接 , , , 分别是 , 的中点,连接 , 则的最大值与最小值的差为( )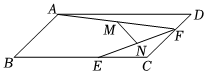 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,CD是△ABC的中线,点E、F分别是AC、DC的中点,EF=2,则BD=.
 10. 如图, , 两点被池塘隔开,在 外选一点 ,连接 和 .分别取 , 的中点 , ,测得 , 两点间的距离为 ,则 、 两点间的距离为 .
10. 如图, , 两点被池塘隔开,在 外选一点 ,连接 和 .分别取 , 的中点 , ,测得 , 两点间的距离为 ,则 、 两点间的距离为 .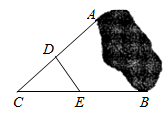 11. 如图,在四边形 中, ,在不添加任何辅助线的情况下,请你添加一个条件 , 使四边形 是平行四边形.
11. 如图,在四边形 中, ,在不添加任何辅助线的情况下,请你添加一个条件 , 使四边形 是平行四边形. 12. 如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=8m,∠A=30°,则DE=m.
12. 如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=8m,∠A=30°,则DE=m.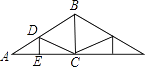 13. 如图,在中,D、E分别是AB、AC的中点,则 .
13. 如图,在中,D、E分别是AB、AC的中点,则 .
三、解答题
-
14. 如图,在ABCD中,点E,F在对角线BD上,且BE=DF.求证:
 (1)、 △ABE≌△CDF; .(2)、四边形AECF是平行四边形.15. 如图,矩形中,点P , Q分别为边上的点, . BD平分 .
(1)、 △ABE≌△CDF; .(2)、四边形AECF是平行四边形.15. 如图,矩形中,点P , Q分别为边上的点, . BD平分 .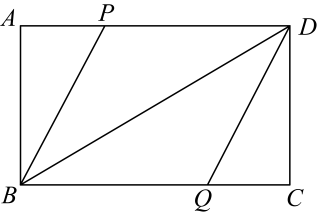 (1)、求证:四边形为菱形;(2)、若 , , 求四边形的面积.
(1)、求证:四边形为菱形;(2)、若 , , 求四边形的面积.四、综合题
-
16. 如图,的中线 , 相交于点G,点P,Q分别是 , 的中点.求证:
 (1)、四边形是平行四边形;(2)、 .17. 如图,在平面直角坐标系中,点A , 点B的坐标分别为 , . 现将点A , 点B分别向上平移2个单位长度,再向右平移1个单位长度,得到点A , 点B的对点C , D , 连接 , , .
(1)、四边形是平行四边形;(2)、 .17. 如图,在平面直角坐标系中,点A , 点B的坐标分别为 , . 现将点A , 点B分别向上平移2个单位长度,再向右平移1个单位长度,得到点A , 点B的对点C , D , 连接 , , . (1)、直接写出点C , 点D的坐标.(2)、①四边形(填“A”或“B”或“C”);
(1)、直接写出点C , 点D的坐标.(2)、①四边形(填“A”或“B”或“C”);A.一定是平行四边形 B.一定不是平行四边形 C.不一定是平行四边形
②求出四边形ABDC的面积.
(3)、在x轴上存在一点F , 若的面积是面积的4倍,直接写出点F的坐标.