人教版初中数学八年级下册 18.1.1 平行四边形的性质同步分层训练培优题
试卷更新日期:2024-03-20 类型:同步测试
一、选择题
-
1. 在中,若的度数是( )A、 B、 C、 D、2. 如图,在中, , , 点D在边上,以 , 为边作平行四边形 , 则的度数为( )
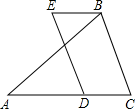 A、 B、 C、 D、3. 如图,四边形为平行四边形,A , C两点的坐标分别是 , , 则平行四边形的周长等于( )
A、 B、 C、 D、3. 如图,四边形为平行四边形,A , C两点的坐标分别是 , , 则平行四边形的周长等于( ) A、 B、 C、 D、4. 如图,▱ABCD的对角线AC , BD交于点O , AE平分∠BAD , 交BC于点E , 且∠ADC=60°,AD=2AB , 连接OE , 下列结论:①∠CAD=30°;②OD=AB;③S平行四边形ABCD=AC•CD;④S四边形OECD=S△AOD:⑤OE=AD . 其中成立的个数是( )
A、 B、 C、 D、4. 如图,▱ABCD的对角线AC , BD交于点O , AE平分∠BAD , 交BC于点E , 且∠ADC=60°,AD=2AB , 连接OE , 下列结论:①∠CAD=30°;②OD=AB;③S平行四边形ABCD=AC•CD;④S四边形OECD=S△AOD:⑤OE=AD . 其中成立的个数是( ) A、1个 B、2个 C、3个 D、4个5. 如图,在中, , , , 则与间的距离为( )
A、1个 B、2个 C、3个 D、4个5. 如图,在中, , , , 则与间的距离为( ) A、5 B、10 C、 D、266. 已知在梯形中,连接 , 且 , 设 . 下列两个说法:
A、5 B、10 C、 D、266. 已知在梯形中,连接 , 且 , 设 . 下列两个说法:①;②
则下列说法正确的是( )
A、①正确②错误 B、①错误②正确 C、①②均正确 D、①②均错误7. 如图,在平行四边形中, , 于E,于F,交于H,、的延长线交于E,给出下列结论: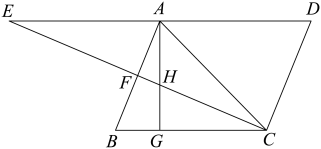
①; ②;
③; ④若点F是的中点,则;
其中正确的结论有( ).
A、4个 B、3个 C、2个 D、1个8. 如图,在中, , , , 点为边上一点,点在的延长线上, . 若四边形是平行四边形,连接 , , 则图中阴影部分的面积为( )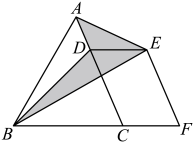 A、24 B、12 C、8 D、6
A、24 B、12 C、8 D、6二、填空题
-
9. 在中,分别为边上的点,若四边形为正方形,则的长为 .10. 如图,在中, , 点在上, . 如果 , 那么°.
 11. 如图,在平行四边形中, , , 以点为圆心,适当长为半径画弧,交于点 , 交于点 , 再分别以点 , 为圆心,大于的长为半径画弧,两弧相交于点 , 射线交的延长线于点 , 则的长是 .
11. 如图,在平行四边形中, , , 以点为圆心,适当长为半径画弧,交于点 , 交于点 , 再分别以点 , 为圆心,大于的长为半径画弧,两弧相交于点 , 射线交的延长线于点 , 则的长是 . 12. 如图,AC为平行四边形ABCD的对角线,AC⊥BC,点E在AB上,连结CE,分别延长CE,DA交于点F.若CE=EF=4,则CD的长为.
12. 如图,AC为平行四边形ABCD的对角线,AC⊥BC,点E在AB上,连结CE,分别延长CE,DA交于点F.若CE=EF=4,则CD的长为. 13. 如图,等边三角形的边长为 , 动点从点出发,沿的方向以的速度运动,动点从点出发,沿的方向以的速度运动,且动点 , 同时出发,其中一点到达终点时,另一点随之停止运动那么运动到第秒时,点 , , 以及的边上一点恰能构成一个平行四边形.
13. 如图,等边三角形的边长为 , 动点从点出发,沿的方向以的速度运动,动点从点出发,沿的方向以的速度运动,且动点 , 同时出发,其中一点到达终点时,另一点随之停止运动那么运动到第秒时,点 , , 以及的边上一点恰能构成一个平行四边形.
三、解答题
-
14. 在平面直角坐标系中, , , , 且 , 满足 .(1)、求点的坐标;(用含的式子表示)(2)、过点作交轴于点 , 当时,
①求的面积;
②若点在直线上,且点的横坐标为5,求点的纵坐标.
15. 如图所示,在形状为平行四边形的一块地ABCD中,有一条小折路EFG.现在想把它改为经过点G的直路,要求小路两侧土地的面积都不变,请在图中画出改动后的小路.
四、综合题
-
16. 如图,在平行四边形ABCD中,∠B=90°,且AD=9cm,AB=4cm,延长BC到点E,使CE=3cm,连接DE.若动点P从A点出发,以每秒2cm的速度沿线段AD运动;动点Q从E点出发以每秒3cm的速度沿EB向B点运动,当点P、Q有一个到位置时,动点P、Q同时停止运动,设点P、Q同时出发,并运动了t秒,回答下列问题:
 (1)、求DE的长(2)、当t为多少时,四边形PQED成为平行四边形;(3)、请直接写出使得△DQE是等腰三角形时t的值17. 【综合探究】已知在平面直角坐标系中的位置如图所示,其中边在轴上且 , 边在轴上且 , 平分交于点 .
(1)、求DE的长(2)、当t为多少时,四边形PQED成为平行四边形;(3)、请直接写出使得△DQE是等腰三角形时t的值17. 【综合探究】已知在平面直角坐标系中的位置如图所示,其中边在轴上且 , 边在轴上且 , 平分交于点 . (1)、请直接写出、两点的坐标: , .(2)、如图1,求点的坐标.(3)、过点作交于点 . 如图2,求面积.(4)、在平面内是否存在一点 , 使得、、、四点组成的四边形是平行四边形,若存在,请直接写出点的坐标:若不存在,请说明理由.
(1)、请直接写出、两点的坐标: , .(2)、如图1,求点的坐标.(3)、过点作交于点 . 如图2,求面积.(4)、在平面内是否存在一点 , 使得、、、四点组成的四边形是平行四边形,若存在,请直接写出点的坐标:若不存在,请说明理由.