人教版数学九年级下册 29.3 课题学习 制作立体模型 同步分层训练 培优题
试卷更新日期:2024-03-20 类型:同步测试
一、选择题
-
1. 如图,是一个正方体的表面展开图,则原正方体中“学”字所在的面相对的面上标的字是( )
 A、我 B、是 C、优 D、生2. 如图所示的平面图形中,其中是四棱锥的侧面展开图的是( )A、
A、我 B、是 C、优 D、生2. 如图所示的平面图形中,其中是四棱锥的侧面展开图的是( )A、 B、
B、 C、
C、 D、
D、 3.
3.如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字是( )
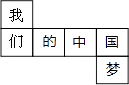 A、的 B、中 C、国 D、梦4. 如图,是一个正方体的表面展开图,则原正方体中与"就"字相对的面上的字是( )
A、的 B、中 C、国 D、梦4. 如图,是一个正方体的表面展开图,则原正方体中与"就"字相对的面上的字是( )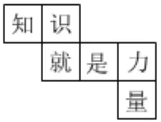 A、知 B、是 C、力 D、量5. 下列图形,是正方体展开图的是( )A、
A、知 B、是 C、力 D、量5. 下列图形,是正方体展开图的是( )A、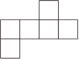 B、
B、 C、
C、 D、
D、 6. 如图一个三级台阶,它的每一级的长宽高分别是5cm,3cm和1cm,点A和点B是这个台阶的两个相对的端点,点A上有一只蚂蚁,想到点B去吃可口的食物,则蚂蚁沿着台阶面爬到点B的最短路程长为( )
6. 如图一个三级台阶,它的每一级的长宽高分别是5cm,3cm和1cm,点A和点B是这个台阶的两个相对的端点,点A上有一只蚂蚁,想到点B去吃可口的食物,则蚂蚁沿着台阶面爬到点B的最短路程长为( ) A、10cm B、11cm C、12cm D、13cm7. 如图,线段AB和CD是正方体表面两正方形的对角线,将此正方体沿部分棱剪开,展成一个平面图形后,AB和CD可能出现下列关系中的哪几种? 、B、C、D四点在同一直线上 正确的结论是( )
A、10cm B、11cm C、12cm D、13cm7. 如图,线段AB和CD是正方体表面两正方形的对角线,将此正方体沿部分棱剪开,展成一个平面图形后,AB和CD可能出现下列关系中的哪几种? 、B、C、D四点在同一直线上 正确的结论是( )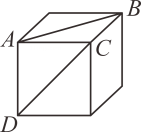 A、 B、 C、 D、8. 明明用纸(如图)折成了一个正方体的盒子,里面装了一瓶墨水,与其它空盒子混放在一起,只凭观察,选出墨水在哪个盒子中( )
A、 B、 C、 D、8. 明明用纸(如图)折成了一个正方体的盒子,里面装了一瓶墨水,与其它空盒子混放在一起,只凭观察,选出墨水在哪个盒子中( )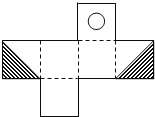 A、
A、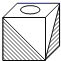 B、
B、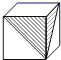 C、
C、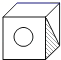 D、
D、
二、填空题
-
9. 如图,该图形折叠成正方体后,与“沉”字相对的字是 .
 10. 一个正方体,六个面上分别写着六个连续整数,且每两个相对面上的两个数的和都相等,如图所示,能看到的所写的数为19,22,23,则这6个整数的和为 .
10. 一个正方体,六个面上分别写着六个连续整数,且每两个相对面上的两个数的和都相等,如图所示,能看到的所写的数为19,22,23,则这6个整数的和为 . 11. 下列图形中是正方体的平面展开图的有(填序号).
11. 下列图形中是正方体的平面展开图的有(填序号).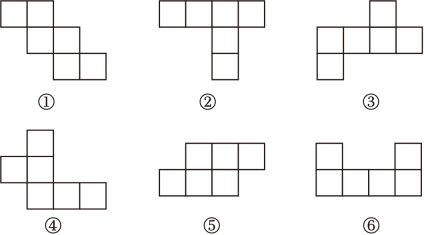 12. 如图,长方体的棱AB长为4,棱BC长为3,棱BF长为2,P为HG的中点,一只蚂蚁从点A出发,沿长方体的表面爬行到点 处吃食物,那么它爬行的最短路程是.
12. 如图,长方体的棱AB长为4,棱BC长为3,棱BF长为2,P为HG的中点,一只蚂蚁从点A出发,沿长方体的表面爬行到点 处吃食物,那么它爬行的最短路程是.
三、解答题
-
13. 长方体的长为20cm,宽为10cm,高为15cm,点B离点C5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖,需要爬行的最短距离是多少?
 14.
14.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
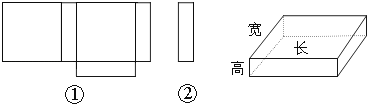
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
四、综合题
-
15. 如图1是边长为 的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).
 (1)、设剪去的小正方形的边长为 ,折成的长方体盒子的容积为 ,直接写出用只含字母 的式子表示这个盒子的高为 ,底面积为 ,盒子的容积 为 ,(2)、为探究盒子的体积与剪去的小正方形的边长 之间的关系,小明列表分析:
(1)、设剪去的小正方形的边长为 ,折成的长方体盒子的容积为 ,直接写出用只含字母 的式子表示这个盒子的高为 ,底面积为 ,盒子的容积 为 ,(2)、为探究盒子的体积与剪去的小正方形的边长 之间的关系,小明列表分析:1
2
3
4
5
6
7
8
324
588
576
500
252
128
填空:① , ;
②由表格中的数据观察可知当 的值逐渐增大时, 的值.(从“逐渐增大”,“逐渐减小”“先增大后减小”,“先减小后增大”中选一个进行填空)
16. 【问题情境】小圣所在的综合实践小组准备制作一些无盖纸盒收纳班级讲台上的粉笔.

【操作探究】
(1)、图1中的哪些图形经过折叠能围成无盖正方体纸盒?(填序号).(2)、小圣所在的综合实践小组把折叠成6个棱长都为的无盖正方体纸盒摆成如图2所示的几何体.①请计算出这个几何体的体积;
②如果在这个几何体上再添加一些相同的正方体纸盒,并保持从上面看到的形状和从左面看到的形状不变,最多可以再添加 个正方体纸盒.