2023-2024学年人教版初中数学九年级下册 29.1 投影同步分层训练 基础题
试卷更新日期：2024-03-20 类型：同步测试
一、选择题
-
1. 小乐用一块长方形硬纸板在阳光下做投影试验，通过观察，发现这块长方形硬纸板在平整的地面上不可能出现的投影是（ ）A、三角形 B、线段 C、矩形 D、正方形2. 一幢4层楼房只有一个窗户亮着一盏灯，一棵小树和一根电线杆在窗口灯光下的影子如图所示，则亮着灯的窗口是（ ）号窗口
A、1 B、2 C、3 D、43. 如图是嘉淇在室外用手机拍下大树的影子随太阳转动情况的照片（上午8时至下午5时之间），这五张照片拍摄的时间先后顺序是（ ）
A、①②③④⑤ B、②④①③⑤ C、⑤④①③② D、⑤③①④②4. 下列是描述小明和小颖在同一盏路灯下影子的图片，其中合理的是（ ）A、
B、
C、
D、
5. 晚上小亮在路灯下散步，在小亮从远处走到灯下，再远离路灯这一过程中，他在地上的影子（ ）A、逐渐变短 B、先变短后变长 C、先变长后变短 D、逐渐变长6. 如图，某剧院舞台上的照明灯P射出的光线成“锥体”，其“锥体”面图的“锥角”是 ， 已知舞台ABCD是边长为6的正方形，AC是正方形ABCD的对角线．要使灯光能照射到整个舞台，则灯P的悬挂高度是（ ）
A、 B、 C、 D、7. 如图，路灯距离地面8米，身高1.6米的小明站在距离灯的底部（点O）20米的A处，则小明的影长为（ ）米．
A、4 B、5 C、6 D、78. 如图，三角板在灯光照射下形成投影，三角板与其投影的相似比为 ， 且三角板的一边长为 ． 则投影三角板的对应边长为（ ）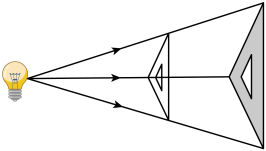
A、 B、 C、 D、二、填空题
-
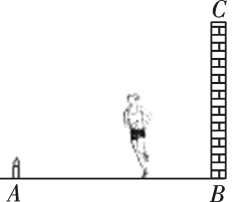
9. 如图，地面上的A处有一支燃烧的蜡烛（长度不计），一个人在A与墙BC之间运动，则他在墙上的投影长度随着他离墙的距离变小而（填“变大”、“变小”或“不变”）．
10. 公元前6世纪，古希腊学者泰勒斯用图1的方法巧测金字塔的高度.如图2，小明仿照这个方法，测量圆锥形小山包的高度，已知圆锥底面周长为62.8 m. 先在小山包旁边立起一根木棒，当木棒影子长度等于木棒高度时，测得小山包影子AB长为23 m（直线AB过底面圆心），则小山包的高为m（π取3.14）.
11. 古希腊数学家泰勒斯曾利用立杆测影的方法，在金字塔塔顶A的影子处直立一根木杆 ， 借助太阳光测金字塔的高度．如图所示，木杆长2米．它的影长是3米，同一时刻测得是201米，则金字塔的高度是米．
12. 如图所示，小王在晚上由路灯走向路灯 ， 当他走到点处时，发现身后自己的影子的顶部刚好接触到路灯的底部；当他向前再步行到达点处时，发现身前自己的影子的顶部刚好接触到路灯的底部.已知小王的身高是 ， 两个路灯之间的距离为 ， 且两路灯的高度相同，则路灯的高度为.
13. 如图是某风力发电机示意图，其相同的三个叶片均匀分布，每个叶片长 ， 即水平地面上的点在旋转中心的正下方 ， 即当风力发电机叶片外端点离地面的高度最大时，若垂直于地面的木棒与影长的比为： ， 则此刻风力发电机的影长为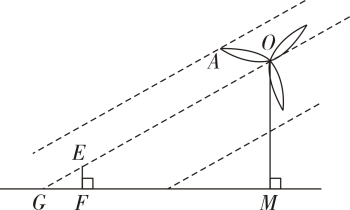
三、解答题
-
14. 如图，小树AB在路灯O的照射下形成投影BC ．
(1)、此光源下形成的投影属于 ． （填“平行投影”或“中心投影”）(2)、已知树高AB为2m，树影BC为3m，树与路灯的水平距离BP为4.5m．求路灯的高度OP ．15. 为了测得一棵树的高度 ， 一个小组的同学进行了如下测量：在阳光下，测得一根与地面垂直、长为1米的竹竿的影长为0.8米．同时发现这棵树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上（如图），测得墙壁上的影长为1.5米，落在地面上的影长为3米．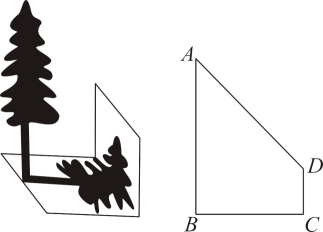
(1)、该小组同学是利用投影的有关知识进行计算的；（填“平行”或“中心”）(2)、求这棵树的高度 ．四、综合题
-
16.
如图，在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD，它们都与地面垂直，为了测得电线杆的高度，一个小组的同学进行了如下测量：某一时刻，在太阳光照射下，旗杆落在围墙上的影子EF的长度为2米，落在地面上的影子BF的长为10米，而电线杆落在围墙上的影子GH的长度为3米，落在地面上的影子DH的长为5米，依据这些数据，该小组的同学计算出了电线杆的高度．
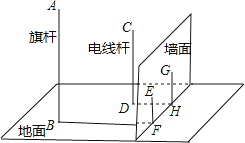(1)、该小组的同学在这里利用的是 投影的有关知识进行计算的；(2)、试计算出电线杆的高度，并写出计算的过程。
17. 如图，一根灯杆上有一盏路灯A，路灯A离水平地面的高度为9米，在距离路灯正下方B点15.5米处有一坡度为的斜坡 ， 如果高为3米的标尺竖立地面上，垂足为F，它的影子的长度为4米．
(1)、当影子全在水平地面上（图1），求标尺与路灯间的距离；(2)、当影子一部分在水平地面上，一部分在斜坡上（图2），求此时标尺与路灯间的距离为多少米？