人教版数学九年级下册 28.2 解直角三角形及其应用同步分层训练 培优题
试卷更新日期:2024-03-20 类型:同步测试
一、选择题
-
1. 从一艘船上测得海岸上高为42米的灯塔顶部的仰角是30度,船离灯塔的水平距离为( )A、 米 B、 米 C、21米 D、42米2. 如图是拦水坝的横断面,堤高为米,斜面坡度为: , 则斜坡的长为( )
 A、米 B、米 C、米 D、米3. 一配电房示意图如图所示,它是一个轴对称图形.已知BC=6m.∠ABC=α.则房顶A离地面EF的高度为( )
A、米 B、米 C、米 D、米3. 一配电房示意图如图所示,它是一个轴对称图形.已知BC=6m.∠ABC=α.则房顶A离地面EF的高度为( )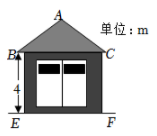 A、 B、 C、 D、4. 如图,在离铁塔100米的处,用测角器测得塔顶的仰角为 , 测角器高为1.4米,则铁塔的高为( )
A、 B、 C、 D、4. 如图,在离铁塔100米的处,用测角器测得塔顶的仰角为 , 测角器高为1.4米,则铁塔的高为( ) A、米 B、米 C、米 D、米5. 如图,与 , 直角顶点重合于点 , 点在上,且 , 连接 , 若 , , 则长为( )
A、米 B、米 C、米 D、米5. 如图,与 , 直角顶点重合于点 , 点在上,且 , 连接 , 若 , , 则长为( ) A、 B、 C、 D、6. 如图,坡角为的斜坡上有一棵大树(垂直于水平地面),当太阳光线与水平线成角沿斜坡照下时,在斜坡上树影的长为30米,则大树的高为( )
A、 B、 C、 D、6. 如图,坡角为的斜坡上有一棵大树(垂直于水平地面),当太阳光线与水平线成角沿斜坡照下时,在斜坡上树影的长为30米,则大树的高为( )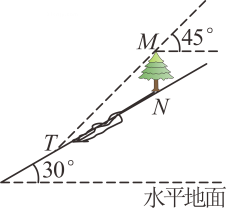 A、米 B、米 C、米 D、米7. 如图,若和的面积分别为 , , 则=( )
A、米 B、米 C、米 D、米7. 如图,若和的面积分别为 , , 则=( ) A、5:8 B、8:5 C、1:1 D、2:78. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H,给出下列结论:①∠DHF=4∠FDP;②△DFP∽△BPH;③PD2=PH•CD;④ . 其中正确的有( )个
A、5:8 B、8:5 C、1:1 D、2:78. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H,给出下列结论:①∠DHF=4∠FDP;②△DFP∽△BPH;③PD2=PH•CD;④ . 其中正确的有( )个 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
9. 如图,用4个全等的直角三角形拼成正方形,古人用它证明了勾股定理,这个图被称为“弦图”.若“弦图”中大正方形面积为20,tana=2,则小正方形的面积为.
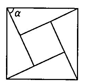 10. 某市为改善交通状况,修建了大量的高架桥.一汽车在坡度为的笔直高架桥起点开始爬行,行驶了15米到达点 , 则此时汽车离地面的高度为米.
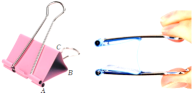
10. 某市为改善交通状况,修建了大量的高架桥.一汽车在坡度为的笔直高架桥起点开始爬行,行驶了15米到达点 , 则此时汽车离地面的高度为米. 11. 如图,长尾夹的侧面是△ABC , 当AC与AB张开到互相平行时,达到最大夹纸厚度,已知AB=AC=15mm , ∠ACB=70°,则这个长尾夹最大夹纸厚度为 mm .
11. 如图,长尾夹的侧面是△ABC , 当AC与AB张开到互相平行时,达到最大夹纸厚度,已知AB=AC=15mm , ∠ACB=70°,则这个长尾夹最大夹纸厚度为 mm .(结果精确到1mm)
【参考数据:sin70°=0.94,cos70°=0.34,tan70°=2.75】
 12. 如图,在△ABC中,∠ACB=90°,∠B=30°,BC=4 , 点P是直角边BC上一动点(点P不与B,C重合),连接AP,将线段AP绕点A顺时针旋转60°得线段AD,连接CD,则线段CD的最小值是 .
12. 如图,在△ABC中,∠ACB=90°,∠B=30°,BC=4 , 点P是直角边BC上一动点(点P不与B,C重合),连接AP,将线段AP绕点A顺时针旋转60°得线段AD,连接CD,则线段CD的最小值是 . 13. 如图,已知 , 点在线段上,是底边长为6的等腰三角形且 , 以为边在的右侧作矩形 , 连接 , 点是的中点,连接 , 则线段的最小值为 .
13. 如图,已知 , 点在线段上,是底边长为6的等腰三角形且 , 以为边在的右侧作矩形 , 连接 , 点是的中点,连接 , 则线段的最小值为 .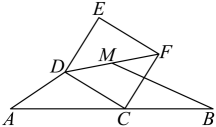
三、解答题
-
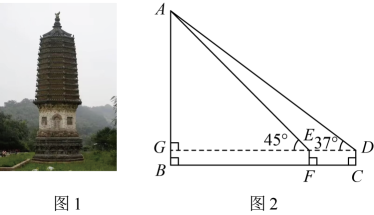
14. 某校组织九年级学生参加社会实践活动,数学学科的项目任务是测量银山塔林中某塔的高度 , 其中一个数学兴趣小组设计的方案如图所示,他们在点C处用高1.5m的测角仪测得塔顶A的仰角为 , 然后沿方向前行7m到达点F处,在F处测得塔顶A的仰角为 . 请根据他们的测量数据求塔高的长度大约是多少.(参考数据: , , , , , . )
 15. 如图1,已知线段AB,AC,线段AC绕点A在直线AB上方旋转,连结BC,以BC为边在BC上方作Rt△BDC,且∠DBC=30°.
15. 如图1,已知线段AB,AC,线段AC绕点A在直线AB上方旋转,连结BC,以BC为边在BC上方作Rt△BDC,且∠DBC=30°.
(1)、若∠BDC=90°,以 AB为边在AB上方作Rt△BAE,且∠AEB= 90°,∠EBA = 30°,连结DE,用等式表示线段AC与DE的数量关系是.(2)、如图2,在(1)的条件下,若 DE⊥AB,AB=-4,AC=2,求 BC的长.四、综合题
-
16. 如图①,将一个正方形纸片和一个等腰直角三角形纸片放入平面直角坐标系中,点 , 点 , , . 如图②,将纸片绕点顺时针旋转,设旋转角为 .
 (1)、当旋转角为30°时,求此时点E的坐标;(2)、当旋转角为时,连接 , 求的值.(3)、在旋转的过程中,当最大时,求此时的面积(直接写出结果即可).17. 如图,点 , B为x轴上一动点,线段AB的垂直平分线CD交y轴于点D,轴交CD于C,记 .
(1)、当旋转角为30°时,求此时点E的坐标;(2)、当旋转角为时,连接 , 求的值.(3)、在旋转的过程中,当最大时,求此时的面积(直接写出结果即可).17. 如图,点 , B为x轴上一动点,线段AB的垂直平分线CD交y轴于点D,轴交CD于C,记 . (1)、点C的轨迹是
(1)、点C的轨迹是①一条直线;②一条关于y轴对称的折线;③一条抛物线;
(2)、求n与m的关系式;(3)、在B的运动过程中,是否存在是等边三角形,如果不存在请说明理由,如果存在请求出此时C的坐标;(4)、当点O到直线CD距离等于2时,直接写出的值.