人教版数学九年级下册 28.2 解直角三角形及其应用同步分层训练 提升题
试卷更新日期:2024-03-20 类型:同步测试
一、选择题
-
1. 已知在中, , , 则的值为( )A、 B、 C、 D、2. 如图,小明利用标杆测量建筑物的高度,已知标杆的长为1.2米,测得米,米.则楼高是( )
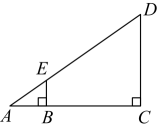 A、6.3米 B、7.5米 C、8米 D、6.5米3. 如图,小明在C处看到西北方向上有一凉亭A,北偏东35°的方向上有一棵大树B.已知凉亭A在大树B的正西方向.若BC=50米,则AB的长等于多少米?
A、6.3米 B、7.5米 C、8米 D、6.5米3. 如图,小明在C处看到西北方向上有一凉亭A,北偏东35°的方向上有一棵大树B.已知凉亭A在大树B的正西方向.若BC=50米,则AB的长等于多少米? A、 B、 C、 D、4. 消防云梯如图所示,AB⊥BC于点B,当点C刚好在点A的正上方时,DF的长是( )
A、 B、 C、 D、4. 消防云梯如图所示,AB⊥BC于点B,当点C刚好在点A的正上方时,DF的长是( ) A、 B、 C、 D、5. 图1是一块矩形材料 ,被分割成三块, , ,将三块材料无缝隙不重叠地拼成图2的形状,此时图2恰好是轴对称图形,则
A、 B、 C、 D、5. 图1是一块矩形材料 ,被分割成三块, , ,将三块材料无缝隙不重叠地拼成图2的形状,此时图2恰好是轴对称图形,则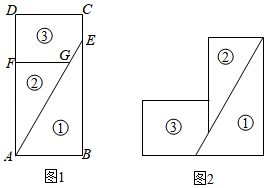 A、 B、 C、 D、6. 在Rt△ABC中,∠C=90°,BC=1,AC= ,那么∠B的度数是( )A、15° B、45° C、30° D、60°7. 在中, , , , 则的面积是( )A、 B、12 C、14 D、218. 电线杆直立在水平的地面上,是电线杆的一根拉线,测得 , , 则拉线的长为( )
A、 B、 C、 D、6. 在Rt△ABC中,∠C=90°,BC=1,AC= ,那么∠B的度数是( )A、15° B、45° C、30° D、60°7. 在中, , , , 则的面积是( )A、 B、12 C、14 D、218. 电线杆直立在水平的地面上,是电线杆的一根拉线,测得 , , 则拉线的长为( )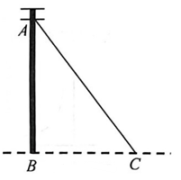 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
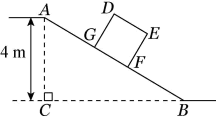
9. 某仓储中心有一斜坡AB,其坡比i=1:2,顶部A处的高AC为4米,B、C在同一水平面上.则斜坡AB的水平宽度BC为米.
 10. 某数学活动小组要测量一建筑物的高度,如图,他们在建筑物前的平地上选择一点A,在点A和建筑物之间选择一点B,测得AB=30m,用高1m(AC=1m)的测角仪在A处测得建筑物顶部E的仰角为30°,在B处测得仰角为60°,则该建筑物的高是.
10. 某数学活动小组要测量一建筑物的高度,如图,他们在建筑物前的平地上选择一点A,在点A和建筑物之间选择一点B,测得AB=30m,用高1m(AC=1m)的测角仪在A处测得建筑物顶部E的仰角为30°,在B处测得仰角为60°,则该建筑物的高是. 11. 如图,在 , , , , 以为直径的半圆交于点 , 则图中阴影部分的面积是 . (结果保留)
11. 如图,在 , , , , 以为直径的半圆交于点 , 则图中阴影部分的面积是 . (结果保留)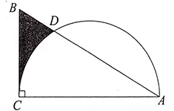 12. 构建几何图形解决代数问题是“数形结合”思想的重要方法,在计算tan45°时,如图,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB , 使BD=AB , 连接AD , 使得∠D=15°,所以tan15°= , 类比这种方法,计算tan22.5°= .
12. 构建几何图形解决代数问题是“数形结合”思想的重要方法,在计算tan45°时,如图,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB , 使BD=AB , 连接AD , 使得∠D=15°,所以tan15°= , 类比这种方法,计算tan22.5°= . 13. 如图,在高楼前点测得楼顶的仰角为 , 向高楼前进米到点,又测得仰角为 , 已知该高楼的高度为米,则米.
13. 如图,在高楼前点测得楼顶的仰角为 , 向高楼前进米到点,又测得仰角为 , 已知该高楼的高度为米,则米.
三、解答题
-
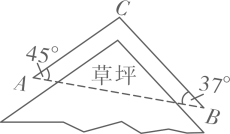
14. 小明上学途中要经过A,B两地,由于A,B两地之间有一片草坪,所以需要走路线AC,CB,如图,在△ABC中,AB=63m,∠A=45°,∠B=37°,求AC,CB的长.(结果保留小数点后一位)
参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, 取1.414.
 15. 图1是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角范围内才能被识别),其示意图如图2,摄像头A的仰角、俯角均为15°,摄像头高度OA=160cm,识别的最远水平距离OB=150cm.
15. 图1是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角范围内才能被识别),其示意图如图2,摄像头A的仰角、俯角均为15°,摄像头高度OA=160cm,识别的最远水平距离OB=150cm.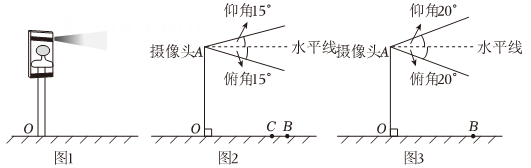 (1)、身高208cm的小杜,头部高度为26cm,他站在离摄像头水平距离130cm的点C处,请问小杜最少需要下蹲多少厘米才能被识别?(2)、身高120cm的小若,头部高度为15cm,踞起脚尖可以增高3cm,但仍无法被识别,社区及时将摄像头的仰角﹑俯角都调整为20°(如图3),此时小若能被识别吗?请计算说明.(精确到0.1cm,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
(1)、身高208cm的小杜,头部高度为26cm,他站在离摄像头水平距离130cm的点C处,请问小杜最少需要下蹲多少厘米才能被识别?(2)、身高120cm的小若,头部高度为15cm,踞起脚尖可以增高3cm,但仍无法被识别,社区及时将摄像头的仰角﹑俯角都调整为20°(如图3),此时小若能被识别吗?请计算说明.(精确到0.1cm,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)四、综合题
-
16. 图1是某小区入口实景图,图2是该入口抽象成的平面示意图.已知入口BC宽3.9米,门卫室外墙AB上的O点处装有一盏路灯,点O与地面BC的距离为3.3米,灯臂OM长为1.2米(灯罩长度忽略不计),∠AOM=60°.
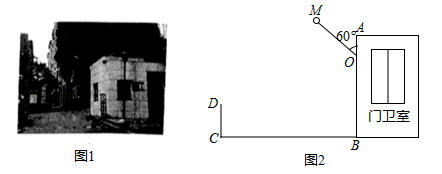 (1)、求点M到地面的距离;(2)、某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据: 1.73,结果精确到0.01米)17. 在中,半径垂直于弦 , 垂足为D, , E为弦所对的优弧上一点.
(1)、求点M到地面的距离;(2)、某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据: 1.73,结果精确到0.01米)17. 在中,半径垂直于弦 , 垂足为D, , E为弦所对的优弧上一点.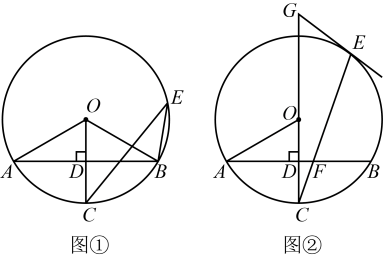 (1)、如图①,求和的大小;(2)、如图②,与相交于点F, , 过点E作的切线,与的延长线相交于点G,若 , 求的长.
(1)、如图①,求和的大小;(2)、如图②,与相交于点F, , 过点E作的切线,与的延长线相交于点G,若 , 求的长.